Obter o deslocamento de um objeto pode ser uma tarefa complicada por conta dos sensores disponíveis para tal necessidade. No caso de usar um acelerômetro, um dos problemas é a dificuldade de entender como fazer a conversão da aceleração em posição. Entretanto, neste post, vamos aprender uma forma de fazê-la para implementar em um projeto por meio do acelerômetro MPU 6050.

(08/2020) O algoritmo foi atualizado e está bastante estável e com uma exatidão razoável. Com movimentos rápidos, fui capaz de obter medições que diferem alguns milímetros do valor real. Mas, para movimentos lentos e distâncias longas, o processo pode ficar pouco exato (varia alguns centímetros do valor real).

Obs: não deixe de ver o post sobre como usar o MPU 6050.

Metodologia

Se quiser pular a parte conceitual introdutória, vá para o tópico “Método dos trapézios”.

Conceito de aceleração

Antes de entender como obter o deslocamento, é importante entender o que é a aceleração. Ela nada mais é do que a variação da velocidade de um objeto em um intervalo de tempo. Seguindo o mesmo raciocínio, a velocidade é a variação da posição em um intervalo de tempo. Considere, por exemplo, um objeto se movendo com uma aceleração constante de 5m/s². Em um intervalo de 1 segundo, sua velocidade aumentará em 5m/s.

Derivada e integral

Certo, mas como converter aceleração para posição? Para entender por completo, vamos pensar o contrário, isto é, converter deslocamento para aceleração.

De acordo com o cálculo, a derivada de uma função em um ponto é a variação instantânea da função naquele ponto. Portanto, a derivada de uma função deslocamento de um objeto nos informará a velocidade instantânea no ponto. Porque a variação instantânea (Δt) da posição em um ponto (x) é justamente a velocidade:

\displaystyle v_{pontual} = \frac{x-x_o}{\Delta t}

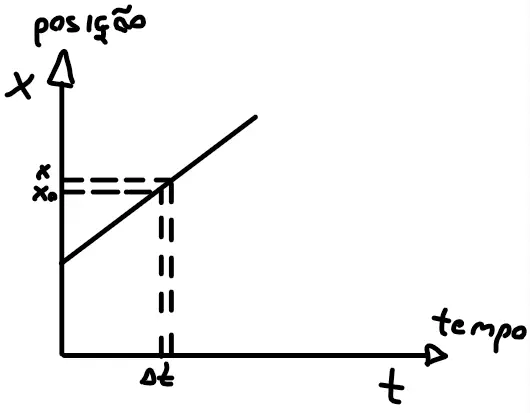
derivada posição pelo tempo

De maneira análoga, se tivermos uma função velocidade em função do tempo, a derivada dela nos daria a aceleração. Tendo isto em mente, podemos utilizar a inversa da derivada para fazer o caminho contrário (converter aceleração para velocidade). E a inversa da derivada é justamente a integral. Sendo assim, calcular a integral de uma função aceleração nos dá a função velocidade. E calcular a integral da função velocidade, nos dá a função posição.

Até ai tudo bem, mas, a partir deste ponto, entra um problema: o acelerômetro informa apenas os valores instantâneos da aceleração e não uma função aceleração por tempo. Desta forma, podemos seguir dois caminhos:

  1. Obter uma equação aproximada da função aceleração com interpolação: de Lagrange, polinomial de Newton ou Interpolação de Gregory-Newton.
  2. Calcular a integral considerando sua definição base: que ela é a área sobre a curva de uma função.

O primeiro método é relativamente complicado de implementar (considerando casos com milhares de amostras). Já o segundo, retorna valores satisfatórios, é mais direto e mais fácil de implementar. A forma como farei para aplicá-lo é utilizando a regra dos trapézios.

Regra dos trapézios

Imagine uma função qualquer e, no meio dela, dois pontos consecutivos. A área debaixo da curva, no intervalo entre esses dois pontos, pode ser calculada com uma aproximação: considerar que a função varia linearmente entre os dois pontos. Dessa forma, esses dois pontos formarão um pequeno triângulo e um quadrado com a base do gráfico. Ou então, um único trapézio. Veja a imagem abaixo para entender melhor:

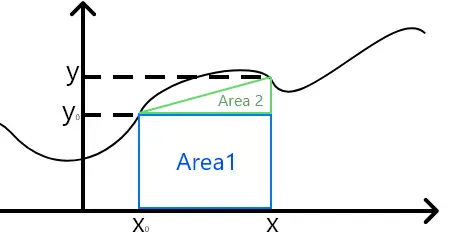
Regra dos trapézios com duas áreas

Considerar que esta área é um trapézio facilita muito as contas, pois calculamos apenas uma área diretamente e não duas. E a área do trapézio é dada como a soma das bases vezes a altura dividido por 2:

\displaystyle \frac{(B+b)*h}{2}

Reescrevendo a equação para os pontos do gráfico, teremos:

Observe que a altura será no eixo x e as bases serão no eixo y.

\displaystyle \frac{(y+y_o)*(x-x_o)}{2}

Para entender melhor, veja a imagem abaixo:

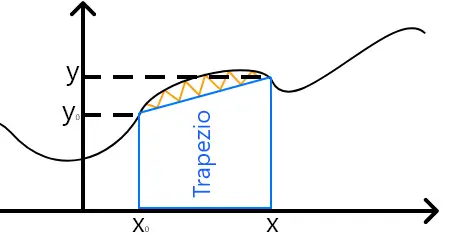
Regra dos trapézios área final

Note a área acima do trapézio, que está indicada em laranja. Quando fazemos esta aproximação de trapézios, estamos desconsiderando totalmente esta área em laranja. Portanto, os resultados não serão 100% exatos. De acordo com os resultados que obtive, percebi que esta aproximação foi pouco perceptível.

Significado da área da curva

Quando utilizamos o método dos trapézios para calcular a área, precisamos saber o que esta área está realmente representando. Imagine a função mostrada no tópico anterior como sendo uma função de aceleração pelo tempo. A área debaixo da curva entre dois pontos informa o quanto a velocidade variou naquele intervalo.

Ou seja, se no ponto x0 a velocidade é 1,0m/s e no ponto x é 3m/s, a área debaixo da curva dará um resultado de 2,0m/s (3-1). Com isso em mente, quando formos calcular a velocidade a partir da área, teremos que ir somando a velocidade encontrada “atualmente” com a velocidade no instante anterior para obtermos o valor da função velocidade e não o quanto a velocidade variou.

Por fim, com a ideia definida, podemos testá-la em uma função qualquer.

Exemplo

Pule para a implementação se não quiser ver a comprovação do método.

Para deixar as últimas explicações mais claras, vamos observar um exemplo prático. Considere a função posição x(t) como sendo:

x(t) = t^3 + t^2 + 1

Aplicando a derivada, conseguimos encontrar a função velocidade v(t). E aplicando a derivada uma segunda vez, obtemos a função aceleração a(t):

v(t) = 3*t^2 + 2*t

a(t) = 6*t + 2

Para simplificar, estou considerando o tempo em segundos e a medida de distância em metros. Agora, vamos supor que queremos encontrar o deslocamento a partir da aceleração, que ocorreu do instante t=0 até t=1s. Para isso, vamos considerar que estamos indo de 0,25 em 0,25 segundos. Portanto, teremos que dividir esse intervalo em 4 pedaços. Com a ajuda do Symbolab, plotei as três funções:

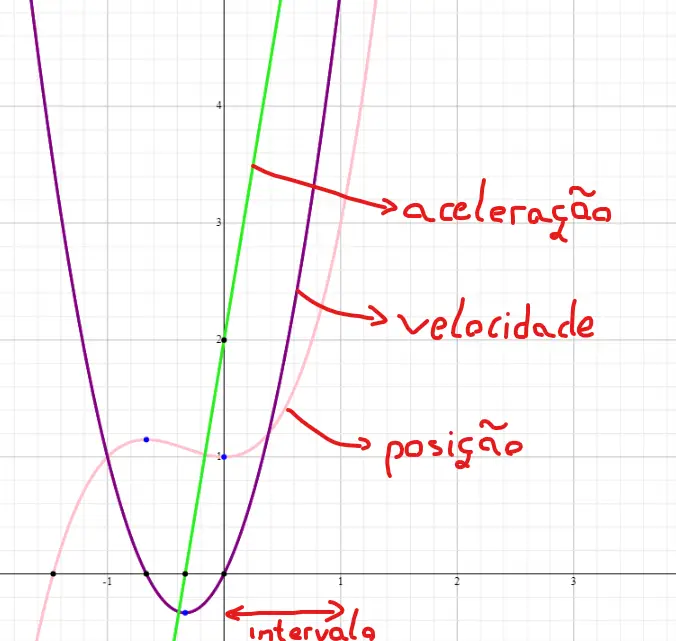
cálculo da área com funções de exemplo

t=0 até t=0,25s

Antes de calcular a velocidade a partir da área da aceleração, vamos calcular o valor real da velocidade e da aceleração no instante t=0,25s para comparação futura.

x(0,25) = 1,078125m

v(0,25) = 0,6875m/s

Agora, para calcular a área debaixo da curva da aceleração, precisamos da aceleração em t=0 e t=0,25s:

a(0) = 2m/s²

a(0,25) = 3,5m/s²

Por fim, basta aplicar a regra dos trapézios:

\displaystyle Area = \frac{(2+3,5)*0,25}{2} = 0,6875

Observe o seguinte: a área encontrada (velocidade) é igual a velocidade no ponto t=0,25s. Como foi dito anteriormente, a área indica a variação da velocidade no intervalo especificado e, como a velocidade no instante t=0 é 0m/s, a velocidade encontrada pela área já é a velocidade do valor da função. E ela, neste caso, é exatamente igual, porque a função aceleração é uma reta, e a área debaixo de uma reta é exatamente um trapézio (ou um triângulo).  Enfim, por motivos teóricos, podemos reforçar o primeiro aspecto fazendo:

v(0,25) = Area + v(0) = 0,6875 + 0 = 0,6875m/s

Com a velocidade encontrada, resta apenas encontrar a posição utilizando a regra dos trapézios com a velocidade da fórmula acima v(0,25) e v(0):

\displaystyle Area2 = \frac{(0+0,6875)*0,25}{2} = 0,089375

Observando o valor de x(0,25), podemos notar uma grande diferença. Mas vale lembrar, novamente, que o valor encontrado acima é a variação da posição no intervalo t=0 até t=0,25s. Portanto, como x(0) = 1, a posição real deslocada é 1,078125 – 1 = 0,078125. Comparando com o valor encontrado, vemos que existe uma imprecisão. Não haverá necessidade de somar o valor da área 2 com x(0), porque o real objetivo deste projeto é saber o deslocamento a partir de um dado instante 0.

t=0,25s até t=0,5s

Calculando os valores reais para comparação futura:

x(0,5) = 1,375m

v(0,5) = 1,75m/s

Calculando a aceleração em t=0,5s:

a(0,5) = 5m/s²

Aplicando a regra dos trapézios para encontrar a variação da velocidade com a(0,25) e a(0,5):

\displaystyle Area = \frac{(3,5+5)*0,25}{2} = 1,0625

Descobrindo v(0,5):

v(0,5) = v(0,25) + Area = 0,6875 + 1,0625 = 1,75m/s

Aplicando a regra dos trapézios para encontrar a variação da posição com Vaproximado(0,25) e o v(0,5) acima:

\displaystyle Area2 = \frac{(0,6875+1,75)*0,25}{2} = 0,3046875

Somando o deslocamento anterior com o atual, teremos um valor próximo do valor real deslocado:

Xaproximado(0,5) = 0,3046875 + 0,089375 = 0,3940625m

Comparando com x(0,5), dá um erro de 0,019m.

t=0,5s até t=0,75s

Calculando os valores reais para comparação futura:

x(0,75) = 1,984375m

v(0,75) = 3,1875m/s

Calculando a aceleração em t=0,75s:

a(0,75) = 6,5m/s²

Aplicando a regra dos trapézios para encontrar a variação da velocidade:

\displaystyle Area = \frac{(5+6,5)*0,25}{2} = 1,4375

Descobrindo v(0,75):

v(0,75) = v(0,5) + Area = 1,75 + 1,4375 = 3,1875m/s

Aplicando a regra dos trapézios para encontrar a variação da posição:

\displaystyle Area2 = \frac{(1,75+3,1875)*0,25}{2} = 0,61178

Somando os deslocamentos anteriores com o atual, teremos um valor próximo do valor real deslocado:

Xaproximado(0,75) = 0,089375 + 0,3046875 + 0,61178 = 1,0058425m

Comparando com x(0,75), dá um erro de 0,021m.

t=0,75s até t=1s

Calculando os valores reais para comparação futura:

x(1) = 3m

v(1) = 5m/s

Calculando a aceleração em t=1s:

a(1) = 8m/s²

Aplicando a regra dos trapézios para encontrar a variação da velocidade:

\displaystyle Area = \frac{(6,5+8)*0,25}{2} = 1,8125

Descobrindo v(1):

v(0,75) = v(0,75) + Area = 3,1875 + 1,8125 = 5m/s

Aplicando a regra dos trapézios para encontrar a variação da posição:

\displaystyle Area2 = \frac{(3,1875+5)*0,25}{2} = 1,0234375

Somando os deslocamentos anteriores com o atual, teremos um valor próximo do valor real deslocado:

Xaproximado(1) = 0,089375 + 0,3046875 + 0,61178 + 1,0234375  = 2,02928m

Comparando com x(1), dá um erro de 0,029m.

Considerações

Foi possível observar que o método funcionou de fato, ignorando a imprecisão. E a cada intervalo analisado, o erro aumentava um pouco. Então, se o tempo total da análise for grande (neste caso foi 1s), a tendência é obtermos um erro maior.

Quanto menor for o intervalo do cálculo (neste caso foi 0,25s), maior será sua precisão. Pois, fazendo isto estaríamos seguindo a real lógica por trás da integral que é dividir a área em infinitos quadrados de tamanho ínfimo. Na implementação, o intervalo será próximo de 0,001s, o que ajuda a melhorar a precisão dos cálculos.

Implementação no Arduino

Lógica escolhida

Seguindo o método explicado anteriormente, é possível implementá-lo no Arduino de diversas formas diferentes. A forma que escolhi foi fazer o cálculo apenas durante o movimento do acelerômetro. Ou seja, se o objeto está parado, nada acontece, mas assim que ele se move, o cálculo começa e só para quando o objeto fica imóvel novamente.

E, a regra dos trapézios é aplicada em “tempo real”. Isto é, vou calculando a velocidade e a distância durante o movimento considerando sempre a aceleração/velocidade anterior e a atual para cada nova medição. Isto ficara mais claro adiante.

Minha intenção não é cobrir a parte da comunicação com o MPU 6050, pois já fiz um post para isso. E farei uso apenas da aceleração em y para simplificar o código e facilitar o entendimento da implementação do método. Mas você pode alterar o eixo da aceleração facilmente.

Variáveis importantes

Ao longo da criação do código, precisei de criar algumas definições e variáveis globais importantes para o funcionamento do código. Adiante explico o significado de algumas delas. Não coloquei todas, pois algumas são mais tranquilas de interpretar.

  • t_amostra

Variável que usarei para medir o tempo entre uma medição e outra. Esse tempo é importante, pois ele será o equivalente a altura do trapézio na hora de usar a regra dos trapézios.

unsigned long t_amostra;

O tempo será medido em microssegundos.

  • t_parado

Esta variável serve para medir por quanto tempo o objeto apresentou uma baixa aceleração para poder declarar que ele está parado.

  • #define STOP_OFFSET 300

O valor desta definição é o limite de aceleração considerado para verificar se o objeto está imóvel. Ou seja, qualquer valor de aceleração abaixo de 300, será considerado como se o objeto não estivesse se movendo. E este é um valor relacionado a medição bruta do sensor (de -32768 a +32767).

Talvez você precise alterá-lo se o seu sensor estiver detectando movimento mesmo estando parado.

  • dist

Como a regra dos trapézios é calculada em “tempo real”, é necessário ter esta variável para ir armazenando a distância deslocada até o momento que o objeto ficar imóvel novamente.

Funções do acelerômetro

Para deixar o código mais fácil de interpretar, resolvi criar algumas funções para comunicar com o MPU6050. E não é preciso entendê-las para compreender a lógica principal do código.

Como são poucas funções, achei melhor criá-las do que utilizar uma biblioteca, já que, com isso, você pode simplesmente copiar o código completo e rodá-lo diretamente sem precisar baixar nada.

Um ponto importante a ser mencionado é a função que está sendo executada no void setup:

mpu6050_offset(-2267, -1111, 504);

Esta função serve para definir os valores dos offsets de calibração da aceleração. Ela recebe 3 parâmetros, cada um correspondente a um dos eixos do sensor. A forma como obtive estes parâmetros foi utilizando esta biblioteca (bastou rodar o código de exemplo IMU_ZERO). De todo modo, não pretendo entrar em detalhes sobre isso aqui.

Se você não pretende procurar como fazer isto, pode comentar/apagar esta linha. Mas saiba que, um valor errado do offset pode fazer a aceleração apresentar um valor bem distante do real.

Conversão e processamento das medidas

Para aplicar corretamente o procedimento estudado, não posso simplesmente utilizar o valor bruto de aceleração do sensor. Preciso, primeiro, convertê-lo em uma unidade convencional (m/s² no caso).

Como disse no post sobre o acelerômetro, o valor retornado pelo MPU6050 varia entre -32768 e 32767, cada um representando -2g e 2g respectivamente. Sendo assim, tenho que remapear os valores medidos para se encaixarem entre -2 e +2.

Utilizar a função map para este propósito não funciona corretamente, pois ela trabalha apenas com valores inteiros. Como estamos convertendo grandes números para um intervalo tão pequeno, fica claro que teremos que utilizar números decimais. Portanto, peguei a fórmula que fica dentro da função map e utilizei ela diretamente:

aux_ac = ((aux_ac + 32768.0) * 4.0/65536.0 – 2.0) * 9.81;

Como 1g equivale a 9,81m/s², bastou multiplicar o valor da conversão (-2g a 2g) por 9.81 no fim.

Obs: os valores das medições das acelerações são números inteiros. E levando em conta o que foi falado acima, foi preciso criar uma variável float para guardar valores decimais da conversão. No caso, isto é feito por meio da variável aux_ac. Por padrão, ela é igualada à aceleração em y, mas isto pode ser alterado facilmente trocando para o eixo desejado:

float aux_ac = float(ac_y);

Fim do movimento

Assim que o código detecta que o objeto ficou imóvel, ele printa o valor deslocado e zera ele. Isto é feito nesta parte:

1
2
3
4
5
6
7
8
9
10
11
12
if (parado)
{
  if(dist != 0.0)
  {
    Serial.println("Distância deslocada (em y): ");
    // A função retorna o valor em metros,
    // então multiplica por 100 para converter para centímetros
    Serial.print(dist*100, 2);
    Serial.println(" cms em y.");
  }
  dist = 0.0;
}

Portanto, se você deseja fazer algo com a distância deslocada, é só criar o seu código neste trecho. Repare que o valor calculado é em metros e o código multiplica ele por 100 para apresentá-lo em centímetros.

Função ‘calculo_trapezio’

Como foi dito, esta função faz o cálculo do deslocamento usando a regra dos trapézios. E o valor antigo da aceleração e da velocidade é armazenado dentro da própria função utilizando o modificador static.

1
2
static float last_acel = 0.0;
static float last_vel = 0.0;

O fato das variáveis terem o modificador static, faz com que seus valores sejam mantidos entre uma chamada da função e outra. Mas, como pode ser visto acima, na primeira vez que a função é executada, o valor delas é 0.

Além destas, a função cria mais duas variáveis importantes, uma para armazenar o valor da velocidade atual e outra do tempo em segundos entre as medições:

1
2
float vel;
float t = (float)tempo/1000000.0;

A variável t pega o intervalo entre as medições (tempo em microssegundos) e converte para segundos. Eu poderia ter feito esta conversão na hora de calcular a velocidade/distância, mas assim facilita a visualização do cálculo feito adiante.

Enfim, a regra dos trapézios está sendo aplicada de fato nestas duas linhas:

1
2
vel = last_vel + (last_acel + acel) * t / 2.0;
dist = dist + (last_vel + vel) * t / 2.0;

Não tem muito o que comentar aqui, pois o cálculo acima foi visto no início deste post. O importante de observar é que estamos somando a velocidade do ponto anterior à velocidade atual. Isto, porque a “velocidade atual” é na verdade a variação da velocidade, conforme foi comentado anteriormente. E o mesmo se aplica à distância.

O restante do código que não foi abordado pode ser compreendido pelos comentários ou pela análise dos comandos.

Circuito

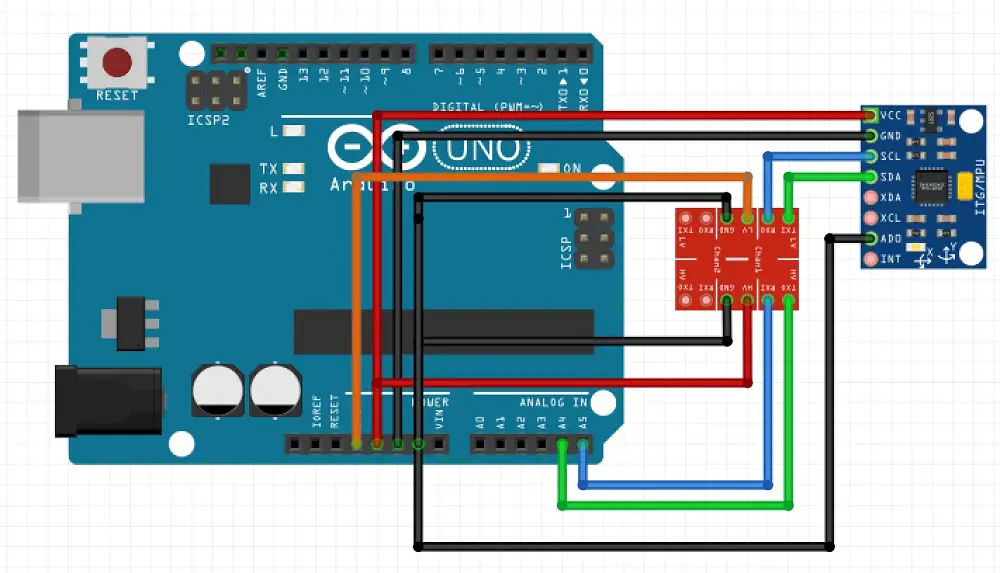
Um pequeno comentário a respeito da ligação dos pinos do acelerômetro pode ser encontrado no post sobre o assunto.

Código completo

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
#include "Wire.h"

// ----- Definições -----
// Endereço do MPU6050 para o pino AD0 em baixa
#define MPU_ADDR  0x68

// Limite de aceleração para objeto parado
#define STOP_OFFSET  300

// ----- Protótipo das funções -----
uint8_t mpu6050_init();
void mpu6050_offset(int16_t cal_ac_x, int16_t cal_ac_y, int16_t cal_ac_z);
void mpu6050_write(uint8_t address, int16_t val, uint8_t size);
int16_t mpu6050_read(uint8_t address, uint8_t size);


// ----- Variáveis globais -----
// Variavel para armazenar o tempo entre cada amostra
unsigned long t_amostra = 0;
// Variaveis para verificar se o objeto está parado
unsigned long t_parado = 0;
bool parado = true;
// Variavel para guardar a distancia deslocada
float dist = 0;

void setup()
{
  Serial.begin(9600);
 
  // Inicializa a comunicação com o MPU6050
  // definindo os offsets de calibração para a
  // aceleração em x, y e z respectivamente
  uint8_t resp = mpu6050_init();

  if (!resp)
  {
    Serial.println("Falha na conexão do MPU6050");
  }
  else
  {
    Serial.println("MPU6050 conectado");
  }

  // Calibração
  // Comente esta linha se você não sabe os valores do seu sensor
  mpu6050_offset(-2267, -1111, 504);

  t_amostra = micros();
}

void loop()
{
  // Variaveis para armazenar o valor medido
  //int16_t ac_x = mpu6050_read(0x3B, 2);
  int16_t ac_y = mpu6050_read(0x3D, 2);
  //int16_t ac_z = mpu6050_read(0x3F, 2);

  // Cria uma variável auxiliar para manipular o valor de aceleração
  // Mude para o eixo desejado
  float aux_ac = float(ac_y);

  // ----- Detecção de objeto parado -----
  // Aceleração baixa e mais de 50ms constante
  if(fabs(aux_ac) < STOP_OFFSET && abs(millis() - t_parado) > 50)
  {
    parado = true;
   
    t_amostra = micros();
  }
  else if(fabs(aux_ac) >= STOP_OFFSET)
  {
    t_parado = millis();
    parado = false;
  }

  // ----- Conversão do valor de aceleração -----
  // Converte o valor medido para m/s^2
  aux_ac = ((aux_ac + 32768.0) * 4.0/65536.0 - 2.0) * 9.81;

 
  // ----- Calculo da distancia deslocada -----
  //Se está parado
  if (parado)
  {
    if(dist != 0.0)
    {
      Serial.println("Distância deslocada (em y): ");
      // A função retorna o valor em metros,
      // então multiplica por 100 para converter para centímetros
      Serial.print(dist*100, 2);
      Serial.println(" cms em y.");
    }
    dist = 0.0;
  }
  // Está se movendo
  else
  {
    // Calcula o tempo percorrido
    t_amostra = micros() - t_amostra;
 
    dist = calculo_trapezio(dist, aux_ac, t_amostra);
   
    t_amostra = micros();
  }
}

/*
 * Calcula em tempo real a distância percorrida pela regra do trapézio
 * Parâmetros:
 *  - dist - distância que está sendo calculada
 *  - acel - aceleração medida atualmente
 *  - tempo - tempo em microssegundos gasto desde a ultima medição
 */
float calculo_trapezio(float dist, float acel, unsigned long tempo)
{
  // Armazena o ultimo valor de aceleração e velocidade dentro da própria
  // função declarando a variável como static (no 1º momento ela será 0)
  static float last_acel = 0.0;
  static float last_vel = 0.0;
 
  float vel;
  // Converte o tempo para um valor em segundos
  float t = (float)tempo/1000000.0;

  // Se o movimento acabou de começar, reinicia a velocidade e a aceleração
  if(dist == 0.0)
  {
    last_vel = 0.0;
    last_acel = 0.0;
  }

  // Calculo utilizando a regra do trapézio
  // Soma a velocidade anterior
  vel = last_vel + (last_acel + acel) * t / 2.0;
 
  dist = dist + (last_vel + vel) * t / 2.0;
 
  // Atualiza os valores antigos de aceleração e velocidade
  last_acel = acel;
  last_vel = vel;

  return dist;
}


// ----- Funções para comunicar com o MPU6050 -----

/*
 * Inicia a comunicação com o MPU6050 e retorna 1 se for bem sucedida
 */
uint8_t mpu6050_init()
{
  Wire.begin(); //Inicia a comunicação I2C
 
  // Lê o endereço do mpu para verificar se ele está conectado
  // se não estiver, sai da função  
  uint8_t id = mpu6050_read(0x75, 1);

  if(id != MPU_ADDR)
  {
    return 0;
  }

  // Define a fonte de clock do sensor para maior estabilidade
  // 0x6B = registrador PWR_MGMT_1
  // 4 = Clock externo (32.768kHz)
  // 5 = Clock externo (19.2MHz)
  mpu6050_write(0x6B, 4, 1);

  return 1;
}

/*
 * Define os valores de offset do MPU6050
 * Parâmetros:
 *  - cal_ac_x: ofsset de calibração da aceleração em x
 *  - cal_ac_y: ofsset de calibração da aceleração em y
 *  - cal_ac_z: ofsset de calibração da aceleração em z
 */
void mpu6050_offset(int16_t cal_ac_x, int16_t cal_ac_y, int16_t cal_ac_z)
{
  // Acel x
  mpu6050_write(0x06, cal_ac_x, 2);

  // Acel y
  mpu6050_write(0x08, cal_ac_y, 2);
 
  // Acel z
  mpu6050_write(0x0A, cal_ac_z, 2);
}

/*
 * Escreve em um registrador do MPU6050
 * Parâmetros:
 *  - address: endereço do registrador
 *  - val: valor a ser escrito no registrador
 *  - size: quantidade de bytes para escrever (o máximo são 2)
 */
void mpu6050_write(uint8_t address, int16_t val, uint8_t size)
{
  Wire.beginTransmission(MPU_ADDR);
  Wire.write(address);
  if(size == 2)
  {
    Wire.write(val >> 8); // MSByte
  }
  Wire.write(val & 0xFF); // LSByte
  Wire.endTransmission();
}

/*
 * Retorna o valor de um registrador (ou dois consecutivos) do MPU6050
 * Parâmetros:
 *  - address: endereço do registrador
 *  - size: quantidade de bytes para ler (o máximo são 2)
 */
int16_t mpu6050_read(uint8_t address, uint8_t size)
{
  int16_t data = 0;

  Wire.beginTransmission(MPU_ADDR);
  Wire.write(address);
  Wire.endTransmission(false);
 
  Wire.requestFrom(MPU_ADDR, size);
  if(size == 2)
  {
    data = Wire.read() << 8;
  }
  data |= Wire.read();

  return data;
}

Considerações finais

O funcionamento do projeto pode ser comprovado pelo vídeo abaixo. Acabei utilizando o NodeMcu para não ter que usar nenhum conversor de nível lógico, mas o Arduino deve funcionar da mesma forma.

Como pôde ser visto, além da distância calculada ter sido bem próxima da real (talvez 1mm de diferença), o algoritmo é capaz de informar o sentido da variação. No caso do vídeo, para direita é negativo e para esquerda positivo.

Pelo que percebi, o código funciona bem para movimentos que começam e terminam rápido (menor que 1 segundo). E o cálculo de movimentos mais demorados fica mais impreciso, mas ainda bem razoável. Enfim, o vídeo abaixo apresenta alguns comentários envolvendo o projeto e suas características.

Não posso esquecer de mencionar o blog Engenheirando, que foi de onde tirei a ideia deste post há cerca de 1 ano atrás.

Acelerômetro MPU6050 com o Arduino