É comum estudar sinais de tensão em corrente contínua e corrente alternada em contextos separados. Entretanto, um mesmo sinal pode ter características dos dois e é isto que veremos neste post.
Ao longo do post estarei tratando sobre sinal elétrico analógico de TENSÃO. O sinal de corrente é similar ao de tensão e varia dependendo apenas dos componentes que estão presentes no circuito: o capacitor adianta a corrente e indutor atrasa ela.
Se quiser aprender a diferença do sinal analógico para o digital, veja este post.
Sinais puramente alternados e puramente contínuos
Tensão média
Antes de definir e diferenciar os sinais contínuos e alternados, é importante ter em mente o conceito de tensão média.
A tensão média nada mais é que a média aritmética da tensão ao longo de um período específico. No caso de sinais periódicos, que repetem sua forma a cada período T, a média é calculada ao longo do período do sinal (T).
Já no caso de sinais constantes, a média pode ser calculada dentro de um período qualquer que faça sentido para o cálculo.
Portanto, a fórmula da tensão média é uma somatória da tensão ao longo do período dividida pelo próprio período:
Sendo Vin(t) a função da tensão analisada, que é uma função que pode ou não variar com o tempo (t).
Com esta definição em mente, vamos analisar a tensão média nos dois tipos de sinais:
Sinais puros de corrente alternada
Um sinal puro de corrente alternada deve ser periódico e deve ser simétrico em relação ao eixo x. Isto é, se a parte positiva for espelhada para baixo, o resultado deve ser igual à parte negativa. Veja um exemplo abaixo:
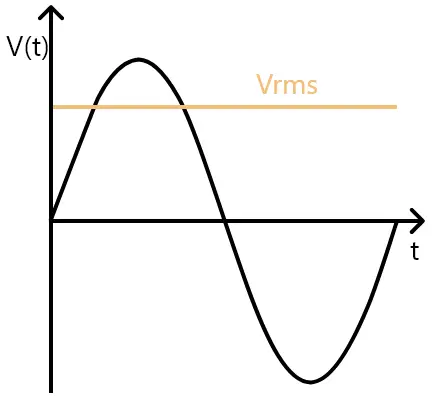
Alguns exemplos de sinais de corrente alternada: senoide; cossenoide; onda quadrada que varia entre +- tensão de pico; onda triangular que também varia entre +- tensão de pico.
A partir da definição do primeiro parágrafo, já podemos concluir qual o valor de tensão média dos sinais de corrente alternada. Se a parte positiva do sinal é igual à parte negativa, quer dizer que a área sob a curva das duas é igual.
O que muda é que a área da parte negativa será negativa. E, como a integral pode ser definida como a área sob a curva, então podemos concluir que:
Como A2 (área parte negativa) é igual a A1, porém com sinal negativo:
Portanto, concluímos que a tensão média de todo sinal puramente alternado é igual a 0.
Se você estiver com um pé atrás em relação à análise acima, basta resolver a integral para um sinal qualquer (senoide por exemplo):
Neste caso Vin = Vmax*sen(ωt).
Vmax é constante, portanto sai da integral. E, T = 2π.
Integral de seno = -cosseno…
Sinais puros de corrente contínua
Um sinal de corrente contínua puro será um sinal constante ao longo do tempo. Veja um exemplo abaixo:
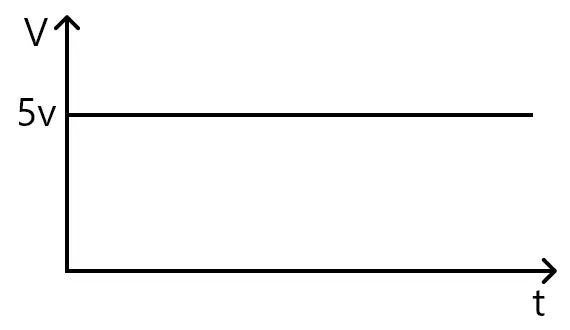
Portanto, para calcular a tensão média, fica mais simples. Como o sinal não possui explicitamente um ponto de começo e de fim, podemos pegar um período qualquer.
Assim como o caso anterior, seguindo pela definição de integral de área sob a curva, podemos achar Vmed facilmente. Considerando T = 1 (não interessa tanto a unidade):
Com o resultado anterior, podemos concluir que um sinal puramente contínuo terá sempre a tensão média igual a tensão do próprio sinal para qualquer ponto ao longo do tempo. Isto é: Vin(t) = Vmed.
Componentes do sinal
O conceito de componentes diz respeito às partes que formam o sinal.
Fazendo uma paralelo: um ponto no plano cartesiano (xy) possui duas componentes: uma componente em x e outra em y. Se o ponto está localizado em (3, 5), quer dizer que a componente x é 3 e a componente y equivale a 5.
Ou seja, x e y são partes do ponto e, juntas, formam o ponto.
No caso do sinal elétrico, as componentes são sinais de tipos diferentes. E esses tipos são justamente o sinal alternado puro e o contínuo puro.
Sinal elétrico
O sinal elétrico é composto por uma componente alternada e por uma contínua. Mesmo sendo composto pelas duas, uma delas pode acabar sendo nula (assim como o exemplo do ponto quando x=0 ou y=0).
No caso da corrente contínua constante, a componente alternada é nula. E, no caso do sinal puro de corrente alternada, a componente contínua é nula.
Com estas definições em mente, fica fácil imaginar um sinal que possui os dois tipos de componentes não nulos. A título de exemplo, vamos combinar uma senoide 10Vpico (1Hz) com um tensão constante 5v:
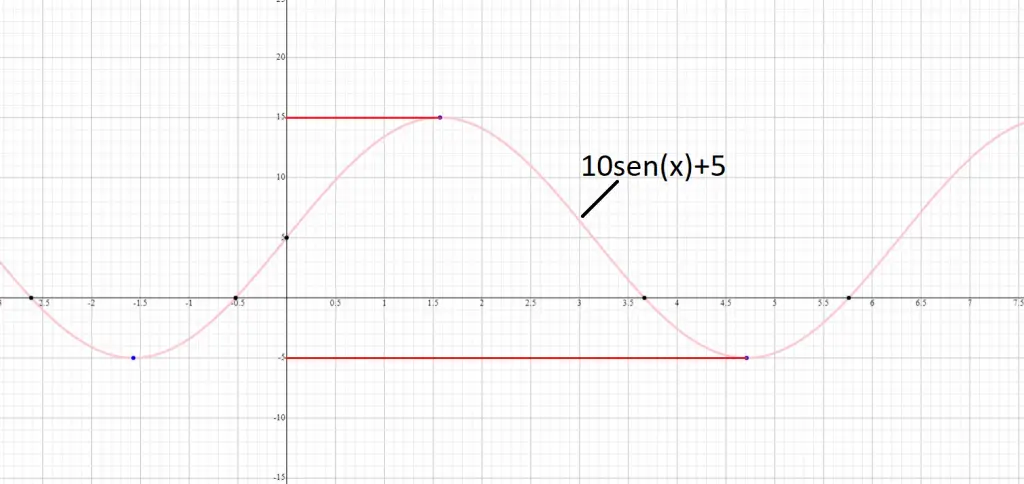
O que aconteceu foi que a senoide foi deslocada 5v para cima. Repare, pelas linhas vermelhas, que a tensão de pico agora é 15V e a tensão mínima é -5V.
E, lembrando que a componente alternada não precisa ser necessariamente um senoide.
De acordo com o que vimos, é relativamente simples identificar a componente alternada e a contínua no sinal acima, considerando que não sabemos a fórmula do sinal. Mas como poderemos descobri-la em sinais mais complexos? É isto que veremos abaixo:
Identificando a componente contínua
Conforme vimos, um sinal puramente alternado possui tensão média igual a 0. Por outro lado, a tensão média de um sinal contínuo é a própria tensão do sinal. Ou seja, é muito fácil identificar sinais puros a partir deste parâmetros.
E, com estas duas informações, podemos concluir que a tensão media de um sinal qualquer sempre será sempre igual à componente contínua do mesmo.
No mundo real, qualquer voltímetro ou multímetro que meça tensão contínua informa, na verdade, o valor da tensão média do sinal que ele está lendo.
Portanto, se um determinado sinal possui tensão média diferente de 0, quer dizer que ele possui componente contínua. E se ele não for constante, significa que ele possui componente alternada.
Separando as duas componentes
Considerando as informações do tópico anterior, podemos pensar em algumas formas de obter as duas componentes separadas.
Como a componente contínua é constante ao longo do tempo, para extraí-la, basta utilizar um filtro passa-baixa. Ele removera o sinal de “alta” frequência da componente alternada e deixará passar apenas a componente contínua (baixa frequência), pois, teoricamente, sua frequência é igual a 0.
De forma análoga, para extrair a componente alternada, basta utilizar um filtro passa-alta. Ele removerá o sinal de baixa frequência da componente contínua e deixa passar o sinal de alta frequência da alternada.
Nos osciloscópios, quando configuramos a leitura do canal em acoplamento AC, estamos tirando a componente contínua do sinal. Isto é feito com a ajuda de um filtro (capacitor).
Uma outra forma de extrair a componente alternada é ligando uma fonte de tensão em série com o circuito. E ela deve ter o mesmo valor da tensão média e deve ser ligada contrária ao sinal.
No exemplo do sinal 10sen(x) + 5, a tensão média é 5 e bastaria ligar uma fonte de tensão de 5V contrária a este sinal para obter apenas a componente alternada, pois o 5V da fonte ia subtrair o 5V do sinal 10sen(x) + 5 e sobraria apenas o sinal 10sen(x).
Uma utilidade desta separação é a análise separada da componente alternada para observar o Ripple do sinal.
Múltiplas componentes contínuas e alternadas
Um sinal elétrico pode possuir mais de uma componente contínua e mais de uma componente alternada.
Se ele possuir duas componentes contínuas, será impossível distingui-las, pois irá parecer que o sinal possui uma única componente contínua que na verdade é a soma do valor das duas componentes. O mesmo ocorrerá se o sinal tiver duas componentes alternadas de MESMA frequência.
Entretanto, se houverem duas componentes alternadas de frequências diferentes, elas podem ser separadas sim, também com a ajuda de filtros.
No caso da separação de componentes alternadas, tocamos no conceito de série de Fourier: qualquer sinal pode ser decomposto em uma soma infinita de senoides ou cossenoides de amplitudes e frequências diferentes. Para visualizar melhor esta ideia, veja a imagem abaixo que mostra como a onda quadrada é formada a partir de senoides:

Um bom exemplo está mostrado na imagem abaixo, em que filtrei uma onda triangular (que possui apenas componente alternado) com um filtro passa-baixa e obtive uma senoide de frequência similar à do sinal original. A onda filtrada está deslocada por conta da defasagem provocada pelo capacitor.
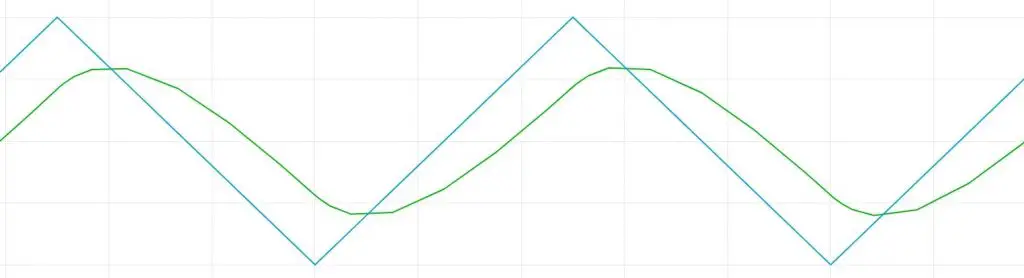
Filtro capacitivo passa-baixa e passa-alta
