Quando trabalhamos com firmwares que precisam executar procedimentos de forma rápida, é possível adotar algumas medidas para ganhar tempo e uma delas é a escolha do tipo de variável adequada. Assim, neste post, analisaremos a diferença de uso das variáveis int e float para verificar qual gera um código mais rápido.
Informações básicas
Contexto
Em algumas aplicações no mundo dos sistemas embarcados, qualquer microssegundo economizado com comandos pode ser realmente útil, pois, normalmente, essas aplicações fazem uso de microcontroladores, os quais devem dar conta de executar inúmeras tarefas em tempo real.
Para exemplificar e ficar menos abstrato, imagine que você está construindo um dispositivo com microcontrolador que lê o sinal de um microfone por um motivo qualquer (criar um walk talk, um gravador ou outro). E seu dispositivo deve ser capaz de capturar sinais próximos aos da faixa de frequência audível pelo ouvido humano (até próximo de 20 kHz). Usando o teorema de Nyquist, podemos dizer que o sinal do microfone deve ser amostrado em no mínimo 40 kHz, o que equivale a 25 microssegundos. Portanto, a cada 25 μs, o microcontrolador deve ler/amostrar o sinal do microfone.
Além da amostragem do sinal, possivelmente também é desejado fazer um processamento, filtrando ruídos ou dando um ganho no sinal. E essa etapa do processamento envolve contas (soma, multiplicação etc) que levam um certo tempo para executar. Se o microcontrolador precisa ler o microfone a cada 25 μs, então as contas não podem, de forma alguma, gastar mais que 25 μs. Diante disso, é importante economizar o máximo de tempo com as contas para evitar problemas. Sem aprofundar muito, um problema que ocorreria caso as contas gastassem mais de 25 μs para executar seria a distorção do sinal do microfone.
Vale lembrar que, além da leitura do microfone, o seu dispositivo também realiza outros procedimentos, como leitura de botões, escrita em um display ou outros. Então, se as contas gastassem exatamente 25 μs, não sobraria tempo para as outras tarefas. Ou seja, é mais um ponto que reforça a necessidade de economia no tempo das contas.
Bem, esse foi um exemplo e no tópico seguinte cito outros casos.
Exemplo de cenários
Vejamos alguns exemplos onde a utilização do tipo de variável deve ser bem pensada:
- Dispositivos que fazem a amostragem de um sinal em uma taxa fixa.
- O exemplo do tópico anterior.
- Um dispositivo que sintetiza e reproduz um som. Veja um exemplo real no vídeo abaixo.
- Neste caso, a amostragem fixa ocorre na reprodução do sinal e não na captação. E as contas são feitas antes da amostragem e não após como no caso do microfone.
- Dispositivos que precisam fazer contas o mais rápido possível.
- Um dispositivo que trabalha com sinais de alta frequência.
- O dispositivo transmissor do vídeo abaixo.
- Ele amostra sinais em suas entradas, modula ambos em um único sinal e coloca o sinal modulado na saída. O ideal seria trabalhar com amostragens fixas igual citado anteriormente, mas o microcontrolador trabalha no limite, então as amostragens acabam sendo definidas pela velocidade com a qual o microcontrolador consegue fazer as contas. Para você ter uma ideia, o tempo total de processamento aqui é na ordem de alguns microssegundos.
- Dispositivos alimentados por bateria.
- Se você diminuir os tempos das contas que seu programa faz, o microcontrolador pode passar menos tempo ‘acordado’ e, consequentemente, economiza mais energia. A diferença pode não ser significativa para muitas aplicações, mas não deixa de ser um fator a ser pensado.
- Esse caso pode se enquadrar no anterior de “fazer as contas o mais rápido possível”, mas decidi separar para evidenciar a questão da bateria.
Por que preocupar com tipo da variável?
Acredito que ficou claro a importância do tempo de execução de contas em algumas aplicações. Mas o que o tipo de variável usada tem a ver com isso? Bem, acontece que o tempo gasto para fazer contas depende do tipo de variável por 2 principais motivos:
- Formato da variável:
O valor dos bits de uma variável do tipo inteira tem relação praticamente direta com o valor representado por ela. Por exemplo, se os bits de uma variável inteira forem iguais a 1001, seu valor será igual a 9. Uma exceção é quando a variável é sinalizada, pois o bit mais à esquerda da variável indica se o valor é negativo ou positivo. De toda forma, para somar um número inteiro não sinalizado, basta somar seus bits diretamente. Praticamente todo processador é capaz de realizar esse tipo de operação gastando apenas 1 ciclo de clock (dependendo do tamanho da variável).
Por outro lado, a variável do tipo float possui a formatação dos bits diferentes, que é justamente o que permite a ela representar os números decimais. Por exemplo, se os bits da variável float forem iguais a 1001, seu valor não será 9, será ~1,26 x 10^-44. Não pretendo explicar qual é o formato da float, mas entenda que somar duas variáveis float não é um processo onde todos os bits são somados diretamente. Então, as contas com float, normalmente, são desmembradas em diferentes instruções, o que envolve um maior tempo gasto pelo processador.
Outro motivo da diferença de velocidade do tipo de variável é arquitetura do processador em termos das instruções que ele computa e se ele é de 8, 16, 32 ou 64 bits.
-
- Instruções do processador
Normalmente, os processadores possuem instruções que permitem trabalhar diretamente com variáveis do tipo inteira, mas não com variáveis do tipo float. Então, as variáveis do tipo float vão exigir mais instruções para realizar contas e, consequentemente, mais tempo. Mais à frente, farei um teste com um microcontrolador STM32 que possui um processador Arm Cortex-M4, o qual possui instruções específicas para variáveis float e veremos qual é a diferença no tempo de execução.
-
- Processador de 8, 16, 32 ou 64 bits
Usualmente, um processador de 8 bits indica que ele é capaz de processar apenas números de 8 bits por vez. Sendo assim, o procedimento de somar dois números de 16 bits gastará mais de uma instrução, pois os números serão somados por partes. Neste contexto, contas com variáveis de 8 bits serão mais rápidas do que contas com variáveis de 16, 32 ou 64 bits. Por exemplo, contas entre inteiros de 8 bits seriam muito mais rápidas do que contas entre floats (32 bits) por conta do tamanho das variáveis e da formatação.
Agora, se o processador for de 16 bits, a princípio, não haveria diferença entre a soma de inteiros de 8 bits ou 16 bits.
Metodologia
Para validar o que foi falado anteriormente, medirei o tempo gasto por um mesmo procedimento feito utilizando apenas variável inteira e utilizando apenas variável do tipo float. Este procedimento simula uma aplicação que realiza a média de 16 valores da leitura AD (lendo microfone e filtrando sinal por exemplo). De forma simplificada, as etapas do procedimento estão adiante:
- Faz a leitura AD 16 vezes e obtém a média.
- Converte o valor lido para tensão.
O procedimento será feito em um Arduino UNO, que possui um processador de 8 bits, e em um STM32F303CBT6, que possui um processador de 32 bits (ARM Cortex-M4). O tempo gasto será medido com a ajuda da função “micros()” no Arduino e com a ajuda da função “HAL_GetTick()” no STM32. No caso, será medido o tempo total para executar o procedimento 16000 vezes com o objetivo de obter uma medição mais exata. Então, será feito algo próximo do que está mostrado abaixo:
1 2 3 4 5 6 7 8 | tempo_inicial = micros(); for(i = 0; i < 16000; i++) { procedimento(); } tempo_final = micros() - tempo_inicial; |
Considerações
- Para eliminar o tempo gasto na inicialização das variáveis, elas serão criadas com o escopo global.
- A própria leitura AD introduz um atraso nos procedimentos. Então, tanto no Arduino UNO, quanto no STM32, a leitura AD será simulada pela leitura direta do valor do registrador AD. Ou seja, o procedimento não funciona na prática, mas ainda assim é capaz de fornecer um bom comparativo entre as variáveis int e float.
- Como o Arduino UNO é de 8 bits, dá pra imaginar, por conta do que foi falado anteriormente, que existiria uma grande diferença nas contas entre inteiros de 8 bits e floats (32 bits). Para diminuir essa diferença, as contas no procedimento com inteiros utilizarão variáveis de 32 bits (uint32_t ou unsigned long).
Função com variável inteira
Adiante está apresentado a função do procedimento que utiliza apenas variáveis do tipo uint32_t.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | void test_int() { tensao_i = 0; // Lê a tensão 16 vezes e faz uma média for(j = 0; j < 16; j++) { // Arduino: tensao_i += (uint32_t)((ADCH << 8) | ADCL); // STM32: tensao_i += (uint32_t) (READ_BIT(ADC1->DR, ADC_DR_RDATA)); } // x >> 4 é a mesma coisa que dividir x por 16 tensao_i = tensao_i >> 4; // Converte a leitura AD para tensao // 5000/1023 = 5 arredondando para cima tensao_i = tensao_i*5; } |
Função com variável inteira
Adiante está apresentado a função do procedimento que utiliza “apenas” variáveis do tipo float. Na realidade, a variável ‘j’ do for é do tipo inteira assim como no procedimento anterior. O foco aqui é a parte principal do procedimento (média e conversão em tensão), então mantive o ‘j’ igual ao da outra função.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | void test_float() { tensao_f = 0.0; // Lê a tensão 16 vezes e faz uma média for(j = 0; j < 16; j++) { // Arduino: tensao_f += (float)((ADCH << 8) | ADCL); // STM32: tensao_f += (float)(READ_BIT(ADC1->DR, ADC_DR_RDATA)); } tensao_f /= 16.0; // Converte a leitura AD para tensao // 5.0/1023.0 = 0.0048875855 tensao_f = tensao_f*0.0048875855; } |
Função para melhorar a medição
O for que executa o procedimento 16000 vezes gasta um certo tempo por si só para executar. Então, podemos criar uma função com um comando que gasta apenas um ciclo de clock para calcular quanto tempo o for gasta. A instrução escolhida aqui foi o NOP, que gasta 1 ciclo de clock e não faz nada:
1 2 3 4 5 6 7 8 9 10 | // Arduino: void test_nop() { __asm__("nop\n\t"); } // STM32: void test_nop() { asm("NOP"); } |
Medindo tempo gasto - Arduino UNO
Observação possivelmente útil: o clock do Arduino UNO é de 16 MHz.
Incerteza das medições
A função micros(), usada para medir o tempo gasto, tem resolução de 4 μs. Logo, a medição final pode ser indicada como: medição +- 4 μs. Entretanto, a medição diz respeito às 16000 execuções do procedimento, e o tempo gasto para executá-lo 1 única vez é obtido dividindo a medição por 16000.
Por meio desta referencia, podemos assumir que, após a divisão, a resolução, ou incerteza, será igual a 4 μs dividido por 16000, isto é: +-0,00025 μs. Conforme veremos adiante, essa resolução é mais do que suficiente para comprovar a diferença existente entres as contas dos dois tipos de variáveis.
Resultados
Após executar cada função individualmente dentro do for e observar o valor impresso no monitor serial, estes foram os resultados obtidos:
- Função test_nop (obtenção do tempo do for): gastou-se 1,27 μs para executar 1 única vez. Removendo o tempo do comando NOP (0,0625 μs), temos: 1,21 μs.
- Função test_int (procedimento que utiliza variável inteira): gastou-se 47,11 μs para executar 1 única vez. Removendo o tempo do for (1,21 μs), temos: 45,9 μs.
- Função test_float (procedimento que utiliza variável float): gastou-se 158,33 μs para executar 1 única vez. Removendo o tempo do for (1,21 μs), temos: 157,12 μs.
Análise dos resultados
A partir dos resultados, vemos que as contas com a variável do tipo float foram beeem mais demoradas, pois gastaram mais de 100 μs a mais que o procedimento com a variável inteira.
Ou seja, naquele cenário da leitura do microfone, ficaríamos restritos a uma frequência de amostragem máxima de ~21 kHz para o procedimento com uint32_t e a uma frequência máxima de ~6 kHz para o procedimento com float. Obs: também teríamos que considerar a limitação de velocidade do conversor AD para saber a frequência de amostragem limite.
Outro detalhe é que, se esse fosse um código de um dispositivo alimentado com bateria, utilizar a variável do tipo inteiro permitira uma execução 3 vezes mais rápida, e consequentemente, uma maior economia de energia.
Código completo
O código utilizado está mostrado abaixo. A quantidade de vezes que o procedimento é executado (16000) foi parametrizada por um define (N_COUNT).
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 | // Quantidade de vezes que o procedimento é executado // (1 a 65535) #define N_COUNT 16000 // Protótipo das funções void test_nop(); void test_float(); void test_int(); // Variaveis criadas globalmente para a inicialização // não influenciar no tempo gasto uint32_t elapsed; uint16_t i; uint8_t j; uint32_t tensao_i; float tensao_f; void setup() { Serial.begin(9600); } void loop() { elapsed = micros(); for(i = 0; i < N_COUNT; i++) { test_nop(); //test_float(); //test_int(); } elapsed = micros() - elapsed; Serial.println(elapsed); Serial.print("Tempo gasto: "); Serial.print(((float)elapsed)/((float)N_COUNT)); Serial.println(" us"); } // Gasta: 1,27 us para executar void test_nop() { __asm__("nop\n\t"); } // Gasta: 158,33 us para executar void test_float() { tensao_f = 0.0; // Lê a tensão 16 vezes e faz uma média for(j = 0; j < 16; j++) { tensao_f += (float)((ADCH << 8) | ADCL); } tensao_f /= 16.0; // Converte a leitura AD para tensao // 5.0/1023.0 = 0.0048875855 tensao_f = tensao_f*0.0048875855; } // Gasta: 47,11 us para executar void test_int() { tensao_i = 0; // Lê a tensão 16 vezes e faz uma média for(j = 0; j < 16; j++) { tensao_i += (uint32_t)((ADCH << 8) | ADCL); } // x >> 4 é a mesma coisa que dividir x por 16 tensao_i = tensao_i >> 4; // Converte a leitura AD para tensao // 5000/1023 = 5 arredondando para cima tensao_i = tensao_i*5; } |
Medindo tempo gasto - STM32F303CB6
O microcontrolador foi ajustado para usar um clock de 72 MHz com cristal externo e o compilador foi configurado para NÃO otimizar o código gerado.
Incerteza das medições
A função Hal_GetTick(), usada para medir o tempo gasto, tem resolução de 1 milissegundo. Logo, a medição final pode ser indicada como: medição +- 1 ms. Entretanto, a medição diz respeito às 16000 execuções do procedimento e o tempo gasto para executá-lo 1 única vez é obtido dividindo a medição por 16000.
Por meio desta referencia, podemos assumir que a resolução, após a divisão, será igual a 1 ms dividido por 16000, isto é: +-0,0625 μs. É bem pior que no caso do Arduino, mas, conforme veremos adiante, esta resolução é mais do que suficiente para comprovar a diferença existente entres as contas dos dois tipos de variáveis.
Resultados
Após executar cada função individualmente dentro do for e observar o valor medido via debug (monitorando a variável elapsed), estes foram os resultados obtidos:
- Função test_nop (obtenção do tempo do for): gastou-se 0,69 μs para executar 1 única vez. Removendo o tempo do comando NOP (0,0139 μs), temos: 0,68 μs.
- Função test_int (procedimento que utiliza variável inteira): gastou-se 12,89 μs para executar 1 única vez. Removendo o tempo do for (0,68 μs), temos: 12,21 μs.
- Função test_float (procedimento que utiliza variável float): gastou-se 15,75 μs para executar 1 única vez. Removendo o tempo do for (0,68 μs), temos: 15,07 μs.
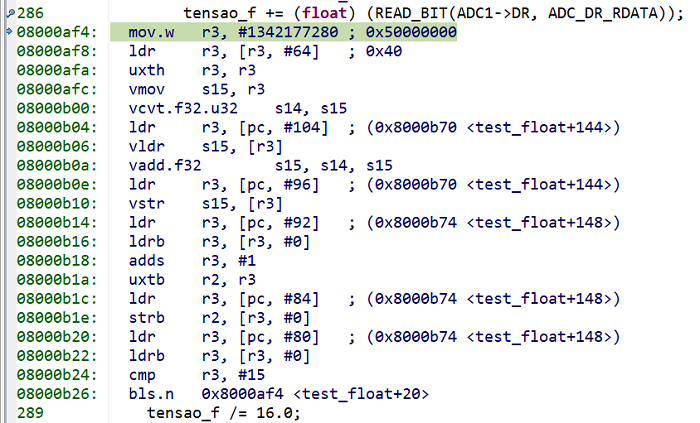
A medição do procedimento com a variável float acima foi feita com o recurso de cálculo via hardware. Conforme falado anteriormente, o processador Arm Cortex-M4 possui instruções para cálculos entre floats. A imagem abaixo mostra as instruções utilizadas pelo programa para fazer a soma entre floats e é possível observar as instruções especiais (vmov, vcvt, vldr etc). Algumas delas gastam apenas 1 ciclo de clock.
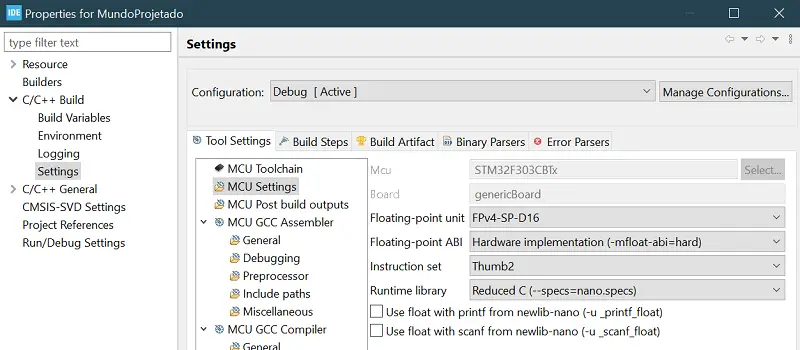
À titulo de comparação, resolvi desabilitar o recurso de calculo de float via hardware por meio das propriedades do projeto. A imagem abaixo mostra ele habilitado (“hardware implementation”).
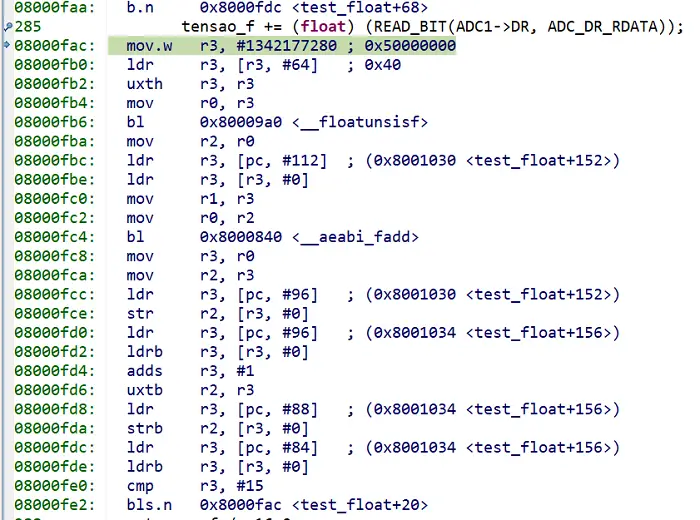
Em seguida, medi novamente o tempo gasto pela função test_float e obtive: 31,88 μs. Removendo o tempo do for (0,68 μs), temos: 31,2 μs. A imagem abaixo comprova que as instruções especiais para float não foram usadas neste caso:
Análise dos resultados
A partir dos resultados, vemos que as contas com a variável do tipo float foram ligeiramente mais demoradas, pois gastaram 2,86 μs a mais que o procedimento com a variável inteira. Pode parecer pouco, mas esse ganho de tempo é crucial em alguns casos, como o do exemplo do segundo vídeo mostrado no início do post (“Sistema FDM didático”).
A pequena diferença foi graças às instruções especiais do processador do STM32 utilizado. Pois, sem utilizá-las, as contas com float gastaram 18,99 μs a mais que o procedimento com a variável inteira (mais que o dobro).
Portanto, em aplicações onde as contas com float são indispensáveis, é válido considerar a utilização de um processador capaz de fazer as contas com float diretamente via hardware.
Código
Não pretendo colocar o código completo aqui, pois a IDE STM32CubeIDE gera muitos outros arquivos com códigos importantes. Então, abaixo estão trechos do código com a criação das variáveis globais, a função main e as funções dos cálculos.
Obs: a conversão da leitura AD pra tensão está igual à forma feita no Arduino por simplicidade, mas o procedimento aqui deveria ser diferente.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 | // Quantidade de vezes que o procedimento é executado // (1 a 65535) #define N_COUNT 16000 // Protótipo das funções void test_nop(); void test_float(); void test_int(); // Variaveis criadas globalmente para a inicialização // não influenciar no tempo gasto uint32_t elapsed; uint16_t i; uint8_t j; uint32_t tensao_i; float tensao_f; /** * @brief The application entry point. * @retval int */ int main(void) { /* USER CODE BEGIN 1 */ /* USER CODE END 1 */ /* MCU Configuration--------------------------------------------------------*/ /* Reset of all peripherals, Initializes the Flash interface and the Systick. */ HAL_Init(); /* USER CODE BEGIN Init */ /* USER CODE END Init */ /* Configure the system clock */ SystemClock_Config(); /* USER CODE BEGIN SysInit */ /* USER CODE END SysInit */ /* Initialize all configured peripherals */ MX_GPIO_Init(); MX_ADC1_Init(); /* USER CODE BEGIN 2 */ /* USER CODE END 2 */ /* Infinite loop */ /* USER CODE BEGIN WHILE */ while (1) { /* USER CODE END WHILE */ /* USER CODE BEGIN 3 */ elapsed = HAL_GetTick(); for(i = 0; i < N_COUNT; i++) { //test_nop(); test_float(); //test_int(); } elapsed = HAL_GetTick() - elapsed; } /* USER CODE END 3 */ } // Gasta: 0,69 us para executar void test_nop() { asm("NOP"); } // Gasta: 15,75 us para executar com FP via hardware // Gasta: 31,88 us para executar sem FP via hardware void test_float() { tensao_f = 0.0; // Lê a tensão 16 vezes e faz uma média for (j = 0; j < 16; j++) { tensao_f += (float) (READ_BIT(ADC1->DR, ADC_DR_RDATA)); } tensao_f /= 16.0; // Converte a leitura AD para tensao // 5.0/1023.0 = 0.0048875855 tensao_f = tensao_f * 0.0048875855; } // Gasta: 12,89 us para executar void test_int() { tensao_i = 0; // Lê a tensão 16 vezes e faz uma média for(j = 0; j < 16; j++) { tensao_i += (uint32_t) (READ_BIT(ADC1->DR, ADC_DR_RDATA)); } // x >> 4 é a mesma coisa que dividir x por 16 tensao_i = tensao_i >> 4; // Converte a leitura AD para tensao // 5000/1023 = 5 arredondando para cima tensao_i = tensao_i*5; } |
Conclusão
Por meio dos testes realizados, foi possível comprovar que procedimentos com variáveis do tipo inteiro são mais rápidos do que procedimentos com variáveis do tipo float. Isso continuou válido mesmo quando utilizamos um processador que possui instruções especiais para fazer contas com floats.
Mesmo que utilizar variáveis inteiras apresentem vantagens em termos de velocidade, elas tem a desvantagem de não ser capazes de representar números decimais de forma satisfatória. Claro, é possível representar o número 5,123 multiplicando ele por 1000 (5123), mas, quando se deseja muitas casas decimais, o número inteiro pode não dar conta de representá-las. Seguindo a ideia de multiplicar por mil, se aparecesse o número 5,1234, ele seria convertido em 5123 e o 4 seria perdido. Então, também tenha isso em mente.
É importante ressaltar que não foram avaliadas otimizações no código a fim de reduzir o tempo dos procedimentos.
Uma outra alternativa à utilização das variáveis inteiras seria o uso de variáveis de ponto fixo, que ainda permitem a representação de números decimais. Veja este documento da ST para mais detalhes.
