Quando vamos montar um sistema digital, pode ser que não tenhamos todas as portas lógicas à disposição. Para resolver este problema, é possível utilizar as portas NAND ou NOR para criar as demais. Portanto, nesta aula, veremos como se dá a universalidade das portas NAND e NOR.
Na aula anterior, projetamos e montamos na prática um circuito combinacional simples.
Informações básicas
O que é a universalidade das portas NAND e NOR
A universalidade das portas NAND e NOR diz respeito ao fato de elas poderem se transformar em qualquer outra porta lógica elementar. Isto é feito configurando elas de diferentes formas para que a tabela-verdade resultante seja igual à de uma outra porta lógica.
A utilidade disto é, como foi dito na introdução do post, substituir uma porta lógica quando ela não for acessível. Isto pode ocorrer quando você não encontrar para comprar ou então quando você precisar testar um circuito, mas não quer comprar uma porta lógica específica.
Desta forma, adiante veremos as correspondências da porta NAND e NOR. E, para entender por completo as equivalências, é importante entender sobre a álgebra booleana.
Porta NAND
Criando porta NOT

A lógica do circuito acima é a seguinte:
=
=
De acordo com a propriedade de multiplicação da álgebra booleana A.A = A.
Criando porta AND

O circuito acima é bem simples de entender, pois é uma junção da porta NOT vista acima com a própria porta NAND:
¬(¬(A.B)) = A.B
Criando porta OR

A lógica do circuito acima advêm da seguinte relação:
=
+
A barra é distribuída ao longo da expressão resultando em uma porta OR com as entradas barradas. E, para converter para a porta OR, basta criar uma porta NOT em cada entrada, assim como foi visto acima.
Porta NOR
A lógica de equivalências para a porta NOR é parecida com o que foi mostrado na porta NAND.
Criando porta NOT

A lógica do circuito acima é a seguinte:
=
=
De acordo com a propriedade de adição da álgebra booleana A+A = A.
Criando porta OR

O circuito acima é bem simples de entender, pois é uma junção da porta NOT vista acima com a própria porta NOR:
¬(¬(A+B)) = A+B
Criando porta AND

A lógica do circuito acima advêm da seguinte relação:
=
.
A barra é distribuída ao longo da expressão resultando em uma porta AND com as entradas barradas. E, para converter para a porta AND, basta criar uma porta NOT em cada entrada, assim como foi visto acima.
Exemplo da universalidade das portas NAND e NOR
Para exemplificar a utilização das conversões mostradas neste post, vamos recriar o seguinte circuito da aula 6 apenas com portas NAND.
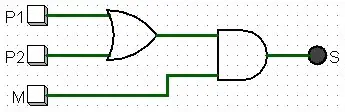
Sua expressão de saída (S) é dada por: S = M(P1 + P2).
Como recriar
Existem duas formas de recriá-lo com as portas NAND:
- Substituindo cada porta lógica pela conversão equivalente.
- Barrando duas vezes a expressão de saída ou aplicando o teorema de De Morgan da álgebra booleana até encontrar uma expressão que envolva apenas operações do tipo NAND.
Como a primeira forma é simples de fazer, pretendo exemplificar com a 2ª forma.
Recriando o circuito
O primeiro passo que tomarei será desmembrar a expressão de saída em termos individuais:
S = M(P1 + P2) = M.P1 + M.P2
Agora, irei aplicar o teorema de De Morgan sobre a expressão OR (envolve os dois termos):
S = ¬( ¬(M.P1 + MP2) )
Distribuindo a barra mais interna:
S = ¬( ¬(M.P1).¬(M.P2) )
Com isto, a expressão de saída fica apenas com expressões do tipo AND ou NAND e não há mais necessidade de aplicar De Morgan. Entretanto, ainda falta converter as expressões AND em expressões do tipo NAND.
Para isto, basta barrar duas vezes estas expressões. Fazendo este procedimento para cada uma das expressões:
M.P1 = ¬(¬(M.P1)) e M.P2 = ¬(¬(M.P2))
Portanto, virou uma NAND barrada de M com P1 e uma NAND barrada de M com P2. Voltando os termos à expressão de saída:
S = ¬( ¬(¬(¬(M.P1))).¬(¬(¬(M.P2))) )
Como cada termo ficou barrado 3 vezes, podemos anular duas barras, pois ainda teremos expressões do tipo NAND:
S = ¬( ¬(¬(¬(M.P1))).¬(¬(¬(M.P2))) ) = ¬( ¬(M.P1).¬(M.P2) )
Ou seja, virou uma expressão do tipo: NAND entre (NAND entre M e P1) e (NAND entre M e P2).
Resultado
Com a expressão convertida do tópico anterior, podemos reconstruir o circuito:


A partir das imagens acima é perceptível que aplicar o 2º método para recriar o circuito resultou em um sistema com apenas 3 portas lógicas. Coisa que não seria verdade se tivéssemos substituído cada porta lógica do circuito original pela conversão equivalente.
Isso porque, a porta OR viraria 3 portas NAND e a porta AND viraria mais 2 portas NAND totalizando 5 portas no circuito. Portanto, é bom optar por reformular a expressão de saída.
Considerações finais
Esta aula foi bem simples e direta, pois o assunto é bem tranquilo de entender mesmo. E ela finaliza o assunto dos circuitos combinacionais. Desta forma, com as aulas passadas, você já tem capacidade de criar sistemas digitais simples de forma completa.
O próximo passo será aprender sobre os decodificadores e codificadores, assunto que envolve os multiplexadores que são circuitos com aplicações bem interessantes.
Codificador e decodificador – Aula 7 – ED

Fantástica explicação!! Irei compartilhar o aprendizado!! Muito obrigado!
Não sou de comentar em posts, mas esse mereceu!!
Caramba, eu é que te agradeço, Luis :D. E espero que os demais posts do site possam te ajudar também.
sabe como representar a porta xor e xnor, pelas portas nand e nor?
Olá, Luiz. Para a porta XOR, esta imagem mostra como fazer usando NANDs e esta imagem mostra usando NORs. E pra fazer a porta XNOR, é só colocar uma porta NOT feita de NAND ou NOR na saída do circuito das imagens anteriores.
uma bosta essa explicação ai nao entendi nada