Este projeto consiste na criação de um robô pêndulo invertido com controlador PID em ambiente de simulação Webots.
Informações básicas
O que é o robô pêndulo invertido
Acredito que o conceito de pêndulo é conhecido para todo mundo e imaginar um pêndulo invertido não é difícil. Mas vamos definir os conceitos para entender melhor o que seria o pêndulo invertido nesse contexto da robótica.
Simplificadamente, o pêndulo consiste em um elemento/objeto preso a um fio que é fixado em uma superfície (ou em um ponto) acima deste elemento. Desta forma, o objeto fica livre para oscilar de um lado pro outro, sendo a gravidade normalmente responsável pela oscilação, pois é ela que puxa o elemento para baixo e faz ele se movimentar em direção à posição central.
Por outro lado, o pêndulo invertido, no contexto da robótica, é um dispositivo em que o ponto de rotação fica na base dele e não na parte superior. Isto é, o elemento que oscila não fica mais pendurado por uma corda. Na prática, pode ser um dispositivo com apenas duas rodas na base que suportam um corpo alongado. Como duas rodas não são suficientes para dar estabilidade ao robô, a tendência natural dele é de tombar para um dos lados. Veja um exemplo abaixo:

Existem outros formatos de pêndulo invertido. O que mostrei acima é apenas um exemplo e é o que usarei no projeto.
Neste sentido, a questão central do robô pêndulo invertido é criar uma forma de deixar o corpo dele sempre em pé (na posição central), mesmo que ele sofra alguma perturbação. Como ele possui duas rodas na base, a forma de garantir a estabilidade do pêndulo é conectar motores às rodas e fazer elas girarem em um sentido ou em um outro dependendo do lado em que o robô está tombando. No gif acima, para evitar o pêndulo cair, as rodas poderiam ser acionadas no sentido anti-horário, criando uma rotação contrária a da queda (ficará claro no tópico sobre o centro de massa).
Ideia do projeto
O objetivo deste projeto é criar um robô pêndulo invertido virtualmente usando o software Webots. Assim, qualquer um lendo o post pode replicar o projeto sem gastar nada, pois o software é gratuito e os arquivos do projeto estão disponibilizados neste link do Github.
Conforme foi falado no tópico anterior, o robô que criaremos possui duas rodas na base e um corpo alongado. Os detalhes da estrutura serão discutidos nos tópicos mais adiante.
Existem várias formas de controlar esse tipo de robô, mas a técnica que usaremos é chamada de controle PID. Se você não sabe do que se trata, recomendo ler o post aqui do site sobre o assunto, pois ele está bem completo, possuindo inclusive um código de exemplo.
Limitações da simulação
Infelizmente não consegui configurar o Webots para reproduzir bem o comportamento do robô pêndulo invertido. Acontece que, por padrão, a simulação fica com o atrito muito baixo, o que impede o robô de se levantar mesmo que a inclinação dele não seja tão significativa (15º por exemplo). Porém, ao adicionar atrito, chega um ponto onde o robô não cai mais quando apresenta uma inclinação pequena (os mesmos 15º de antes).
Em resumo: ou o robô fica impedido de cair, ou ele só consegue se equilibrar se estiver com uma inclinação de poucos graus (+-5º por exemplo). Preferi seguir com a abordagem do atrito, pois é algo mais próximo da realidade no sentido de que o robô conseguirá se equilibrar mesmo quando estiver apresentando uma inclinação significativa (30º). Vale salientar que, na prática, isso exigiria que o chão e as rodas do robô tivessem um alto coeficiente de atrito (rodas de borracha no chão de madeira por exemplo).
Além disso, não consegui fazer o robô apresentar momento angular (inercia de rotação). Por conta disso, o robô não fica oscilando quando o motor está acionado e ele ultrapassa do ponto central. Assim, o controlador P sozinho é capaz de fazer o robô se equilibrar, e a adição do controlador I e D é que faz ele oscilar.
Como na vida real o robô tem momento angular, resolvi criar o projeto com os 3 controladores (P, I e D) para que você possa replicar os passos caso queira implementar o robô na prática.
Apesar de tudo que falei, a simulação ainda é bem interessante de ser observada e pode ser usada como uma plataforma de aprendizado e como um laboratório de testes que não custa nada.
Construindo robô - Estrutura
Não pretendo explicar como usar o Webots, pois foge do foco do post. Pretendo apenas focar nas principais características que o robô precisa ter.
Centro de massa
Se você está pensando em criar esse robô na vida real, o centro de massa é algo que você vai precisar se preocupar, pois ele influencia diretamente na facilidade do controle. Vamos entender o porquê a partir da imagem abaixo que mostra as forças que atuam no robô e dois casos com o centro de massa em pontos diferentes:
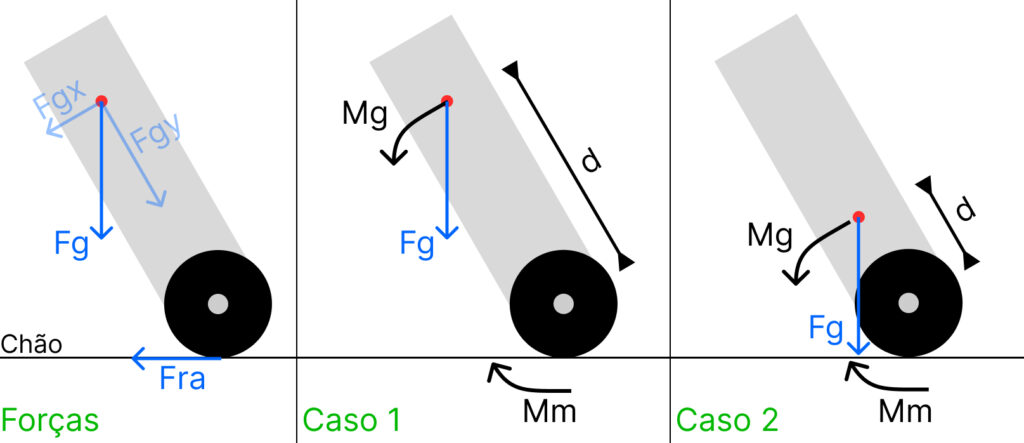
O centro de massa é indicado pela bolinha vermelha, o vetor Fg em azul é a força exercida pela gravidade, Fgx e Fgy são as componentes da força da gravidade, Mg é o torque gerado pela gravidade, Fra é a força de reação do atrito (força de reação é a força contrária à força do atrito) que aparece quando o motor gira no sentido anti-horário e Mm é o torque que o motor produz (gerado pela força Fra). A força Fra e as componentes Fgx e Fgy só foram indicadas no primeiro desenho para não deixar os demais com muita informação. E o torque Mm é gerado no ponto em que Fra está atuando. Desenhei ele fora para deixar o desenho mais limpo.
Obs: a força Fra só aparece quando o motor gira no sentido anti-horário. Se o motor não girar, a roda gira sozinha no sentido horário (pois a componente Fgy da gravidade empurra o robô para direita) fazendo aparecer uma força de atrito no mesmo sentido de Fra. Isto é, seria a força de atrito natural que se opõe à queda do robô.
Diante disso, o momento (torque) exercido pela gravidade nos casos 1 e 2 será o produto da força pela distância do centro de massa ao eixo de rotação. No caso, a força não é exatamente Fg e sim a componente dela que é perpendicular ao corpo do robô (Fgx):
Mg = Fgx * d
Como nos dois casos a massa do robô e o ângulo de inclinação são iguais, Fgx será igual. Entretanto, o que mudará será a distância, que no caso 2 será menor. Ou seja, o momento gerado pela gravidade no caso 2 (centro de massa próximo ao eixo) é menor do que no caso 1.
Para o robô deixar de cair, ele precisa girar na direção em que ele está caindo e gerar um torque contrário com valor (módulo) maior que Mg. Considerando que Mg é menor no caso 2, este também será o caso em que exigira um menor torque do motor para controlar o robô.
Portanto, aproximar o centro de massa do eixo das rodas ajuda a minimizar o esforço dos motores, o que ajuda no controle. Para fazer isso na vida real, você pode construir o robô com a bateria posicionada na parte de baixo, já que ela costuma ser o elemento de maior peso. Ou então você pode adicionar pesos (pedaços de metais densos) na parte de baixo do robô.
No caso do Webots, existe uma propriedade que configura o centro de massa e resolvi deixar ele quase igual ao caso 2 da imagem acima.
Outro detalhe importante é que é possível aumentar o torque do motor (Mm) aumentando o tamanho das rodas. Isso, porque, quanto maior o tamanho da roda, maior será a distância da força de reação do atrito ao eixo de rotação (centro da roda):
Mm = Fra * r
Onde r é o raio da roda.
Sensores
Para poder controlar o robô corretamente, precisamos medir o estado dele. O principal é conseguir saber para qual lado ele está caindo para que possamos acionar o motor no mesmo sentido. Entretanto, apenas saber o lado não é suficiente, pois a velocidade da queda pode variar e sempre acionar o motor com a mesma velocidade pode fazer o robô ficar oscilando de um lado para o outro de forma instável.
Uma ótima forma de saber para qual lado o robô está caindo e também qual a velocidade da queda é utilizar um acelerômetro. Isso, porque, a partir de dados de aceleração nos três eixos, podemos saber qual é a inclinação do robô. Além disso, sabendo a inclinação do robô em cada momento, podemos descobrir a variação da inclinação de um ponto para outro, que seria a velocidade com que ele está caindo (graus por segundo).
O problema do acelerômetro é que, o movimento gerado pelo motor do robô faz a leitura de aceleração variar gerando valores momentâneos de ângulo que não condizem com a realidade. Para isso, é interessante usar também um giroscópio, pois a leitura dele pode ser combinada à do acelerômetro para obtermos um valor da inclinação do robô mais condizente com o real (veremos como isso é feito na parte do código). Alguns sensores como o MPU6050, vêm com a capacidade de acelerômetro e de giroscópio em um único sensor, o que facilita a criação do robô na vida real.
No caso do Webots, é preciso criar cada sensor separadamente. E as caixinhas azul e verde na parte de cima do robô são justamente os sensores.
Motores
O que controlaremos na simulação é a velocidade do motor. Na vida real a ideia seria a mesma para um motor CC comum. No caso, um motor CC pode ser controlado com a ajuda de um driver de potência (ponte H). E o driver de potência por sua vez poderia ser controlado por PWM.
Não tenho uma fonte para afirmar isso, mas acredito que construir o robô usando motores de passo garante uma estabilidade maior. Isso, porque o motor de passo, assim como o próprio nome dele sugere, permite que você movimente o eixo dele em pequenos passos. Com isso, o controle é mais preciso quando comparado a um motor CC comum.
Malha de controle simplificada
Conforme mencionei, o robô será controlado via PID, então o controle dele pode ser simplificado pela malha de controle adiante:
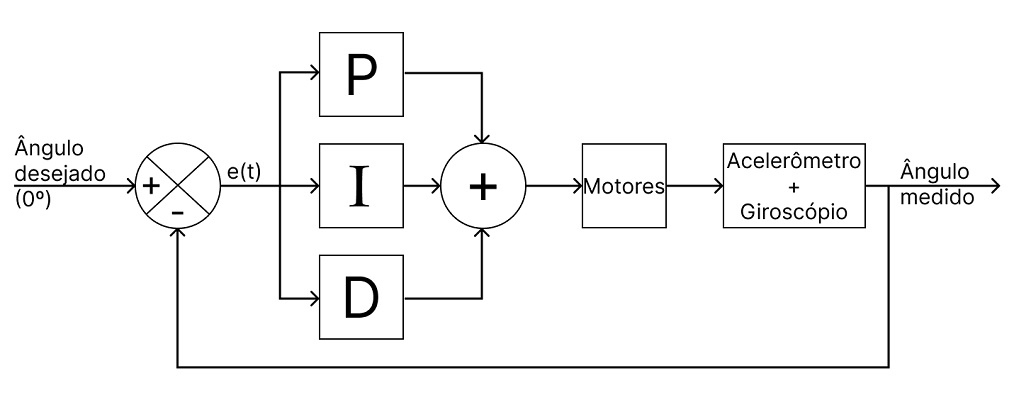
A partir da imagem podemos fazer as seguintes pontuações:
- Como setpoint (ângulo desejado) temos o ângulo de quando o robô está em pé, que considerei como sendo 0º;
- O setpoint menos o ângulo medido gera o erro e(t). Como o setpoint é 0:
- e(t) = – ângulo medido
- A parte do controle PID está simplificada, mas as equações estão explicitadas neste post;
- O controle dos dois motores é simultâneo (o mesmo valor de velocidade é enviado aos dois ao mesmo tempo);
- A leitura do ângulo será melhor detalhada no tópico sobre o código
Construindo robô - Código
Não pretendo explicar sobre o controle PID, pois isto já está explicado em detalhes neste post.
Leitura do acelerômetro e giroscópio
Para transformar os valores do acelerômetro em ângulos, podemos utilizar as seguintes fórmulas:
angulo_1 = \arctan(\frac{leitura_x}{\sqrt{leitura_y^2 + leitura_z^2}})
angulo_2 = \arctan(\frac{leitura_y}{\sqrt{leitura_x^2 + leitura_z^2}})
A fórmula certa a ser usada vai depender de como seu sensor está montado. Para a forma como posicionei o sensor na simulação, usarei a fórmula que mede o ângulo em torno do eixo X (fórmula 2). Explicações e detalhes sobre as fórmulas podem ser encontrados neste material da digikey.
Assim como mencionei no tópico sobre os “Sensores”, o acelerômetro por si só pode fornecer valores de ângulos errados por conta da aceleração momentânea gerada pelo acionamento dos motores. Por conta disso, precisamos combinar a leitura dos dois. Assim, de acordo com esse material bem interessante que achei sobre o assunto, fiz uso da seguinte fórmula:
angulo_{filtrado} = \alpha \times (angulo_{antigo} + leitura_{giroscopio}) + (1 – \alpha) \times angulo_{bruto}
Onde α é uma constante que ajusta o comportamento dessa fórmula que pode ser considerada um filtro. Não pretendo entrar em detalhes sobre ela, pois envolve assuntos complexos como digitalização de sinal, filtros digitais e fusão de sensores. Então, foque apenas no resultado prático da fórmula. No caso, usaremos um α igual a 0,999, que é quase o mesmo usado no link que coloquei.
Etapas do código
O código possui as seguintes etapas:
- Inicialização:
- Dos sensores (acelerômetro e giroscópio);
- Dos motores;
- Das variáveis de controle:
- É preciso calcular o ângulo inicial para achar o erro inicial. Assim, se o robô iniciar em um estado crítico (caindo), ele é capaz de se recuperar rapidamente.
- Se você estiver construindo o robô na vida real com o Arduino, essa etapa iria no void setup.
- Loop principal:
- Calcula o erro atual:
- Procedimento feito de acordo com o que foi exposto no tópico da malha de controle;
- Calcula com qual velocidade (e qual sentido de rotação) acionar o motor no instante atual:
- Conforme está explicado no post sobre controle PID.
- Aciona o motor com a velocidade e sentido de rotação definido no passo anterior:
- Se o ângulo medido estiver com a orientação errada, é possível que o acionamento do motor esteja trocado. Isto é, ele gira no sentido horário quando deveria girar no anti-horário. Como isso ocorreu na simulação, adicionei uma linha no código para trocar o sentido do acionamento;
- Forcei uma limitação no código, pois a simulação pode aceitar valores de velocidade altos, o que foge do comportamento de um motor CC comum.
- Calcula o erro atual:
Descobrindo constantes P, I e D
O processo de descobrir as constantes é um pouco chatinho e envolve modificar as constantes manualmente até chegar no ponto necessário. Existe um algoritmo capaz de, via simulação, testar as constantes de forma progressiva até chegar à valores adequados (não necessariamente ideais). Esse algoritmo é chamado de twiddle. Explicar ele deixaria esse post muito cheio, então pretendo abordar este assunto em outra oportunidade.
Apesar disso, você pode observar uma série de fatores para conseguir ajustar as constantes manualmente de forma eficiente. Para isso, você precisa ter um bom entendimento de cada controlador para entender qual é o efeito esperado ao aumentar ou diminuir a constante de cada um. Sendo assim, é altamente recomendável que você leia o post sobre PID.
Enfim, aqui vai um breve resumo:
- Se o robô não está dando conta de criar a força inicial para evitar de cair, é provável que a constante proporcional (P) esteja baixa;
- Se o robô consegue se contrapor à queda inicial, mas passa do ponto central e cai, é possível que a constante derivativa (D) esteja baixa ou que a constante P esteja alta;
- Se o robô consegue se estabilizar, mas não fica exatamente no ponto central, é possível que a constante integral (I) esteja baixa;
- Se o robô fica oscilando indefinidamente em torno do ponto central, você pode tentar diminuir a constante P ou I.
Um ponto importante: como o sistema é naturalmente instável (o robô cai se nada for feito), o controlador derivativo é fundamental ao garantir a estabilidade do sistema (conforme falado no post do controle PID).
Código completo
O código completo está disponível no Github. Acesse o link para baixar o projeto e testar no seu computador. Ou então apenas leia o código para aprender como o processo foi feito. No caso, fiz duas versões do código: uma em C e outra em Python.
Projeto em funcionamento
Após construir o ambiente de simulação e usar os procedimentos citados para controlar o robô, veja abaixo o resultado que obtive.
Obs: animação em câmera lenta rodando na metade da velocidade real.

E abaixo está um gráfico mostrando a variação do ângulo ao longo do tempo. O eixo y mostra o ângulo em graus e o eixo X o tempo em termos de intervalos de 16 ms (timestep da simulação):
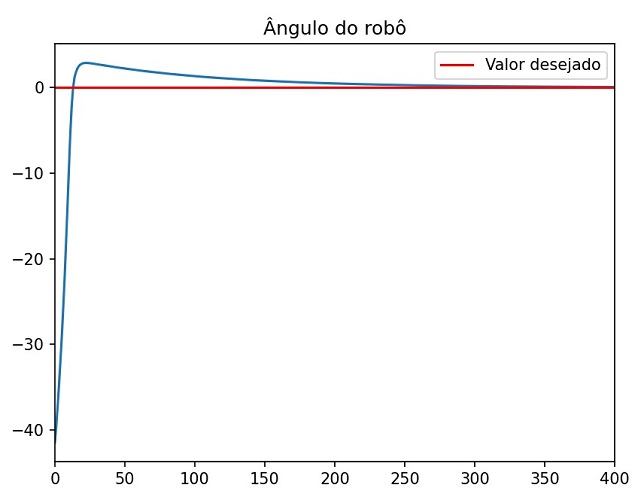
Análise
Diante dos dois resultados apresentados anteriormente, podemos dizer o seguinte:
- O robô foi capaz de se equilibrar com sucesso mesmo iniciando com uma inclinação próxima de 45º:
- Dependendo do coeficiente de atrito do chão, isso não é possível;
- O controlador D tem papel fundamental em garantir a estabilidade desse sistema.
- Em menos de 50 unidades de tempo (800 ms), o robô já foi capaz de ficar em pé (erro menor que 2º);
- O controlador I e D têm grande influência nesta velocidade do regime transitório (quanto maior as constantes, mais rápido).
- Entretanto, o ângulo só ficou menor que 1º após quase 400 unidades de tempo (6,4 segundos):
- Isso é causado pelo controlador I, pois ele deixa o sistema mais lento em regime permanente, mas garante que ele atinja um erro 0 em regime permanente;
- Quanto maior a constante do controlador I, mais lento fica o sistema em regime permanente.
- A resposta do ângulo possui uma oscilação/overshoot que é causado pelos controladores I e P. Quanto maior a constante I ou P, maior será esse overshoot.
Causando perturbações
Por fim, acho interessante mostrar que o controlador é bom o suficiente para manter o robô em pé mesmo sofrendo perturbações, como ser atingido por uma caixa de 1 kg.

É bem impressionante, mas lembre-se que dependendo do atrito do chão do ambiente em que o robô será testado (e do atrito das rodas), ele não conseguirá levantar do chão sozinho.
