A rede neural convolucional é bastante empregada no reconhecimento de padrões em imagens, mas podem ir além. Assim, neste post, aprenderemos o que é a rede neural convolucional, o que podemos criar com ela e como ela funciona. Veremos também alguns assuntos complementares, como o Max Pooling.

Informações básicas

Conceitos prévios

Para as explicações que virão a seguir, vou pressupor que você já tem um conhecimento básico sobre alguns dos principais conceitos de rede neurais, como neurônio artificial, pesos etc. Se não for o seu caso, recomendo assistir um vídeo introdutório que fiz sobre o assunto:

O que é a rede neural convolucional

Dentre as redes neurais artificiais, existem diferentes tipos com aplicações também distintas. Um deles é a Rede Neural Convolucional ou, do inglês, Convolutional Neural Network. Comumente ela é chamada apenas de CNN. Esse tipo de rede é adequada para trabalhar com imagens, sendo capaz de atingir alto desempenho em tarefas visuais complexas, conforme veremos no tópico adiante.

Para entender de fato o que é a CNN e como ela se diferencia da rede neural “básica” (perceptron multicamadas ou MLP), vamos relembrar um pouco sobre a rede MLP com uma arquitetura de exemplo:

Fonte: Wikipedia

Conforme a imagem acima, podemos perceber que os neurônios de qualquer camada da rede MLP, com exceção da de entrada, tem uma relação direta com todos os neurônios da camada anterior. Ou seja, a saída de um determinado neurônio leva em conta os valores de todos os neurônios da camada anterior. E, cada neurônio vai produzir uma única saída.

No caso da CNN, a situação não é a mesma, pois os neurônios dela analisam a camada anterior em pequenos conjuntos e produzem uma saída para cada conjunto analisado. Por exemplo, se a entrada (Input) tem tamanho 12, um neurônio da rede convolucional pode analisar de 3 em 3 valores e gerar uma saída para cada conjunto (4 saídas).

Com isso, o neurônio pode extrair mais informações dos dados ao reconhecer padrões existentes dentro dos conjuntos. Isso fica mais claro se imaginarmos que a entrada (Input) são pixels de uma imagem, pois, dessa forma, a CNN é capaz de analisar trechos da imagem de forma separada. Então, é possível ter ideia do porquê essa rede performa bem em tarefas visuais.

Acredito que não seja um processo muito eficiente explicar o que é CNN abordando o que é convolução, pois o conceito de convolução é um tanto quanto complexo. Esse conceito e outros detalhes serão entendidos quando entrarmos na explicação do funcionamento da rede neural convolucional.

Para que serve a rede neural convolucional

A rede neural convolucional pode ser combinada a outros tipos de redes e aplicada nos seguintes cenários:

  • Reconhecimento de elementos em imagens.
    • Objetos.
    • Faces.
    • Dígitos/caracteres.
    • Palavras completas.
    • Raça de cachorro.
    • Situações de risco.
      • Pessoas com e sem “máscara contra Covid-19”.
  • Detecção de elementos em imagens.
    • Localização de objetos.
    • Localização de pessoas/faces.
    • Localização de textos.
  • Descrição de uma imagem.
  • Reconhecimento da fala.
  • Entre outros.

Como funciona a rede neural convolucional

Para facilitar o entendimento, vamos imaginar que a entrada da rede seja uma imagem de tamanho qualquer. Além disso, vamos pensar apenas em imagens em escala de cinza (1 canal de cor), com cada pixel variando de 0 a 255 (preto a branco).

Conjuntos de dados

Como as imagens são bidimensionais, então faz sentido pensarmos em uma rede neural convolucional que analisa conjuntos de dados em duas dimensões. Isto significa que os conjuntos serão regiões retangulares sequenciais da imagem. Eles começam no canto superior esquerdo da imagem e vão da esquerda para direita. Quando chegam na extremidade direita da imagem, eles retornam para a esquerda deslocados verticalmente. Veja um exemplo abaixo com 25 conjuntos:

Conjuntos da rede neural convolucional separados

O tamanho horizontal e vertical dos conjuntos é algo totalmente personalizado. Você pode criar uma rede que analisa retângulos de tamanho 2×2, 4×2, 3×4, 7×7 pixels etc. No caso da imagem acima, os retângulos são de 40×40. Além disso, os conjuntos podem compartilhar pixels entre si, que é o que normalmente acontece. Assim, o conjunto 2 é um retângulo que fica posicionado poucos pixels à direta do conjunto 1. Isso também ocorre verticalmente quando os conjuntos retornam à extremidade esquerda. Veja um exemplo (só desenhei até o 20):

Conjuntos da rede neural convolucional juntos

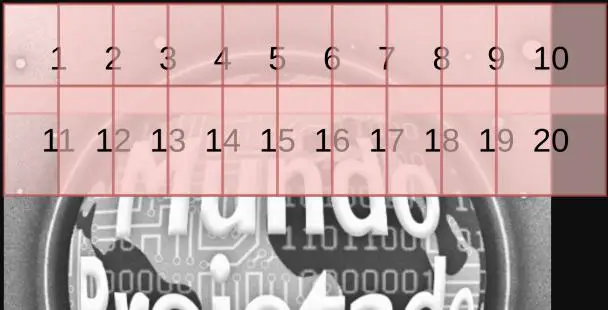
Essa distância entre os conjuntos é constante e recebe o nome de stride, podendo ter valor horizontal e vertical diferentes. No caso da imagem acima, o stride tem valor horizontal 20 e vertical 30. Ou seja, a posição horizontal do conjunto 2 é 20 pixels maior que a posição do conjunto 1 e a posição vertical do conjunto 11 é 30 pixels maior que a do conjunto 1.

A partir da imagem acima, vemos que o conjunto 10 engloba uma região que está fora da imagem. Quando isso ocorre, existem duas possibilidades:

  • Ignorar o conjunto 10.
    • Opção padding=”valid” na biblioteca Keras.
  • Considerar que a região fora da imagem são pixels com valor 0.
    • Opção padding=”same” na biblioteca Keras.

É possível optar por uma das duas opções quando estamos desenvolvendo uma rede neural convolucional.

Pesos, filtros e kernel

Agora que entendemos como os conjuntos são formados, vejamos como o neurônio aplica a convolução em cima deles.

Os neurônios da camada convolucional, também chamados de filtros ou kernel, vão possuir um tamanho fixo de n x m pesos (valores). Sendo que n x m é justamente o tamanho do conjunto de dados abordado no tópico anterior. Isso, porque os conjuntos são gerados a partir do tamanho do kernel.

Com isso, para cada conjunto de pixels da imagem, o neurônio multiplica o valor dos pixels pelo valor do peso correspondente e soma todos eles. Para ficar mais claro, vejamos um exemplo onde o kernel tem tamanho 3×3:

Os números em cima da imagem são os valores dos pixels e os em cima do kernel são os valores dos pesos.

Kernel da rede neural convolucional

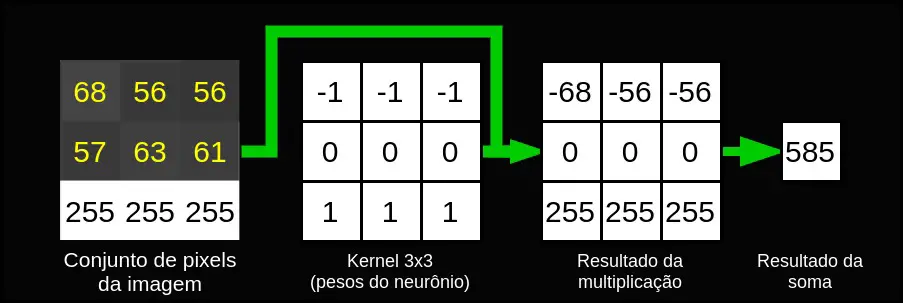
Imaginando que o conjunto de pixels e o kernel são matrizes, é como se ambos fossem multiplicados elemento a elemento (produto Hadamard). E, após a multiplicação, os elementos da matriz resultante são somados. 

Essa operação é justamente a convolução, que, simplificadamente, pode ser definida como a soma do produto entre duas funções. No caso, as funções são o conjunto de pixels e o kernel. Esse conceito ficará menos abstrato no tópico sobre equações.

É importante lembrar que o processo descrito foi o neurônio atuando em apenas um conjunto. Como o neurônio atua em diversos conjuntos de pixels, ele gera várias saídas. No contexto de imagens, podemos interpretar as saídas do neurônio como sendo pixels de uma imagem, cujo tamanho vai depender principalmente do stride. Normalmente, uma camada convolucional possuirá diversos neurônios e cada um irá gerar uma “imagem”. Por conta disso, esse tipo de rede exige um recurso computacional maior do que as redes MLP.

Além disso, dependendo dos valores dos pesos do kernel, a rede é capaz de extrair diferentes características da imagem. No caso acima, os pesos foram colocados de forma que o neurônio é capaz de detectar contornos na imagem. Provarei isso no tópico seguinte. Entretanto, na prática, os valores do kernel são descobertos sozinhos pela rede no processo de treinamento.

Exemplo de neurônio convolucional que detecta bordas

Fiz um programa que executa a convolução de apenas 1 neurônio em uma imagem, cujos pesos foram definidos da mesma forma que a imagem do tópico anterior. No caso, são pesos configurados para detectar bordas verticais. Veja o resultado adiante:

Resultado da rede neural convolucional detectando bordas

Resolvi aplicar um kernel do filtro Scharr horizontal, que também serve para detectar bordas. Veja adiante:

Resultado CNN com filtro Scharr

Obs: Os pixels de uma imagem variam entre 0 e 255 e a convolução pode gerar valores acima e abaixo dessa faixa. Felizmente, a biblioteca OpenCV lida com o mapeamento automaticamente na hora de exibir a imagem de saída.

Caso queira testar, fiz o código utilizando o Python e as bibliotecas Numpy e OpenCV:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
import cv2
import numpy as np

img = cv2.imread("logo.png", cv2.IMREAD_GRAYSCALE)
# O tamanho da imagem de saída não é igual ao de
# entrada, pois ignoro alguns conjuntos. Mas resolvi
# fazer como se fosse, pois não tem diferença prática
imgOut = np.zeros_like(img)

H_IN, W_IN  = img.shape
H_OUT, W_OUT = imgOut.shape

# Detector de bordas
KERNEL = np.array([[-1, -1, -1],
                   [0, 0, 0],
                   [1, 1, 1]])

# Filtro Scharr
KERNEL = np.array([[3, 0, -3],
                   [10, 0, -10],
                   [3, 0, -3]])

N, M = KERNEL.shape

# Stride
S = 1

# Itera sobre as linhas
for i in range(H_OUT):
    if i % 50 == 0:
        print("Processando linha %d/%d" % (i, W_OUT))

    # Itera sobre as colunas
    for j in range(W_OUT):        
        # Pula a linha se o conjunto atual englobar
        # uma região fora da imagem
        if (i*S + N) >= H_IN or (j*S + M) >= W_IN:
            break

        # Convolução
        mult = np.multiply(img[i*S: i*S+ N, j*S: j*S + M], KERNEL)
        soma = np.sum(mult)
       
        imgOut[i][j] = soma

cv2.imshow("Imagem original", img)
cv2.imshow("Saida do neuronio", imgOut)
cv2.waitKey(0)

Equações da rede neural convolucional

De forma simplificada, a operação que cada kernel faz pode ser descrita pela equação adiante:

P_{OUT}(i,j) = \sum_{r=0}^{n-1} \sum_{c=0}^{m-1} P_{IN}(i \times S + r, j \times S + c) \times Pesos_{Filtro}(r,c)

Onde P_OUT (i, j) corresponde ao valor do pixel da imagem de saída (saída do neurônio) na i-ésima linha e j-ésima coluna. P_IN indica os pixels da imagem de entrada, S é o stride, r e c são os índices das linhas e colunas da imagem de entrada respectivamente e, n e m definem o tamanho do kernel. Considera-se que os índices começam em 0.

A fórmula considera apenas um canal de cor da imagem. Se ela for colorida, cada neurônio gerará 3 imagens de saída (outro ponto que explica o alto custo computacional).

Aqui, podemos entender melhor o conceito de convolução, já que a fórmula anterior está num formato mais comum de convolução (somatório de produto).

Seguindo em frente, temos as equações que descrevem o tamanho da imagem de saída dos neurônios de acordo com o stride e outros parâmetros:

Ir_{OUT} = \frac{Ir_{IN} – n}{S} + 1

Ic_{OUT} = \frac{Ic_{IN} – m}{S} + 1

Onde Ir_OUT define a quantidade de linhas da imagem de saída e Ir_IN da imagem de entrada. Ic_OUT define a quantidade de colunas da imagem de saída e Ic_IN da imagem de entrada. Assim como antes, S é o stride e, n e m são relativos à altura e largura do kernel.

As fórmulas acima consideram aquela opção onde os conjuntos que englobam regiões fora da imagem são ignorados. Se eles não forem ignorados, o tamanho da imagem de saída é igual ao da imagem de entrada.

Múltiplas camadas convolucionais

Ideia

Uma arquitetura de rede neural pode combinar diversas camadas convolucionais para permitir um reconhecimento de padrões mais complexos. Isso, porque, a primeira camada é capaz de abstrair características baixo nível (bordas) e as camadas seguintes vão ser capazes de obter características de alto-nível (formas geométricas).

Tanto é que algumas arquiteturas, como a VGG16 (muito usada para reconhecimento de objetos), usa até mais de 10 camadas convolucionais.

Max Pooling e minimização de custo computacional

É comum construirmos arquiteturas com dezenas de filtros em cada camada convolucional. Isso, somado à combinação de múltiplas camadas convolucionais, adiciona um grande custo computacional ao algoritmo. Para tentar minimizar esse custo, emprega-se algumas camadas cujo objetivo é simplificar/reduzir o tamanho da saída gerada por um neurônio.

Um tipo muito empregado é a camada Max Pooling. O funcionamento dela é bem próximo ao da camada convolucional. A diferença é que o Max pooling não possui pesos, pois ele apenas extrai o valor máximo de um conjunto de n x m pixels.

Obs: estou reusando as letras, então n e m aqui não são iguais aos usados anteriormente. 

Ao invés do valor máximo, também pode ser obtida a média destes n x m pixels ou realizar outra operação, mas o nome para isso não é mais Max pooling e sim apenas pooling. 

Assim como a camada convolucional, a camada pooling também possui os parâmetros do tamanho do kernel e do stride. Um exemplo de seu funcionamento pode ser visto na imagem abaixo, que mostra um caso onde o kernel tem tamanho 2 x 2.

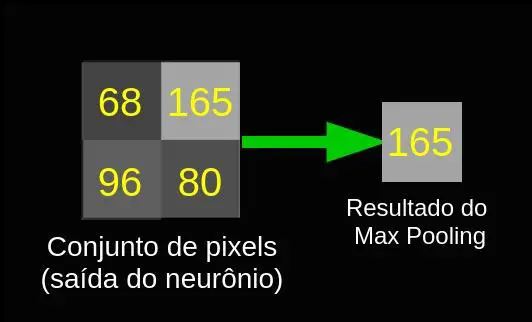
Operação Max Pooling

O resultado prático para a camada Max pooling com kernel e stride de tamanho 2 é uma redução pela metade no tamanho da saída do neurônio convolucional.

Resolvi pegar o resultado daquele código que fiz e aplicar um Max Pooling com kernel e stride de tamanho 2. Veja adiante:

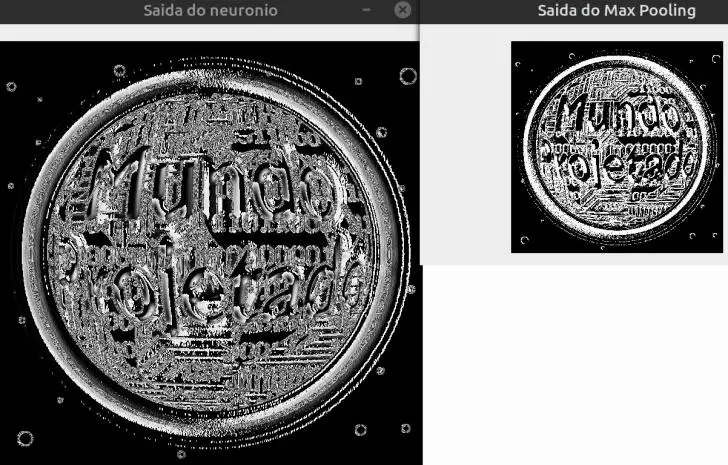
Aplicando Max Pooling na saída do neurônio convolucional

Repare que de fato o tamanho da imagem caiu pela metade. Apesar de alguns detalhes terem se perdido, a redução não comprometeu boa parte das características extraídas.

Rede neural convolucional e MLP

Em tarefas que envolvem o reconhecimento de objetos, é normal que as camadas finais sejam do tipo MLP. Isso, porque a camada de saída desse tipo de rede precisa informar a probabilidade daquela imagem ser um determinado objeto, e a camada convolucional não serve diretamente para tomar essa decisão. Então, emprega-se, normalmente, uma camada MLP com função de ativação ReLU seguida de uma camada MLP com função Softmax para a saída. Veja o caso da arquitetura VGG16 abaixo:

Fonte: ICHI.PRO

Resolvi falar dessa parte para dar uma noção de como a coisa ocorre na prática, mas existem muitos detalhes que não pretendo comentar aqui.

Observações finais

Parte do material apresentado foi retirado do meu TCC, que explora bastante as CNNs. Futuramente, ao final do trabalho, pretendo mostrar como criar algumas das aplicações que citei lá no início do post.

Referência bibliográfica

O texto foi baseado no conteúdo do livro Mãos à Obra: Aprendizado de Máquina com Scikit-Learn & TensorFlow ou, em inglês, Hands-On Machine Learning with Scikit-Learn and TensorFlow. Existe uma versão mais nova que inclui exemplos com a biblioteca Keras. Citei a versão antiga, pois é ela que tenho. Se você tiver interesse em aprender mais sobre aprendizado de máquina de uma forma geral, recomendo bastante a compra do livro.

Reconhecimento de voz – Como fazer?