O multivibrador astável pode ser um circuito simples, mas com utilidades bem interessantes. Sendo assim, vamos aprender o que é o multivibrador astável e como ele funciona.
Informações básicas
É extremamente recomendável a leitura do post sobre o que é o transistor BJT e como utilizá-lo.
O que é um multivibrador astável
O multivibrador astável é um tipo de circuito que oscila constantemente entre dois estados. E, com isto, ele é capaz de gerar um sinal de onda quadrada em sua saída. Um exemplo de sinal gerado está mostrado na imagem abaixo.
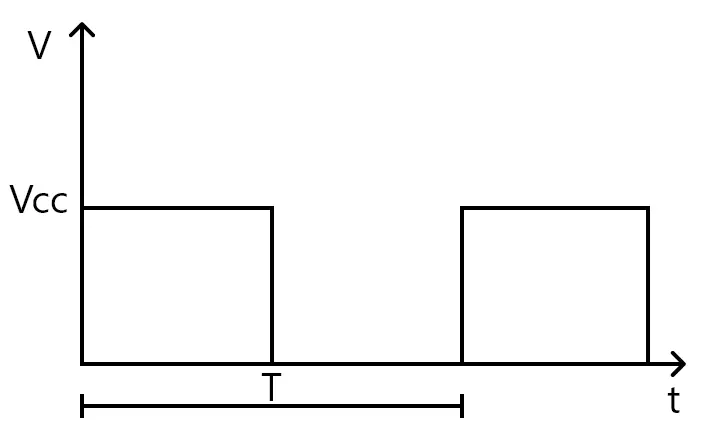
Esse tipo de circuito pode ser feito de algumas formas diferentes, por exemplo com transistores ou então com o circuito integrado 555, como foi explicado neste post. Entretanto, o objetivo desse post é focar no multivibrador astável utilizando transistores de junção bipolar (BJT).
Circuito
Imagine que existem dois circuitos separados que polarizam transistores com uma determinada corrente de base e de coletor. Levando isto em conta, o multivibrador astável nada mais é do que a interligação destes dois circuitos adicionando dois capacitores.
Sendo assim, o circuito típico de um multivibrador astável está mostrado na imagem adiante. Se preocupe em entender apenas as ligações por enquanto.
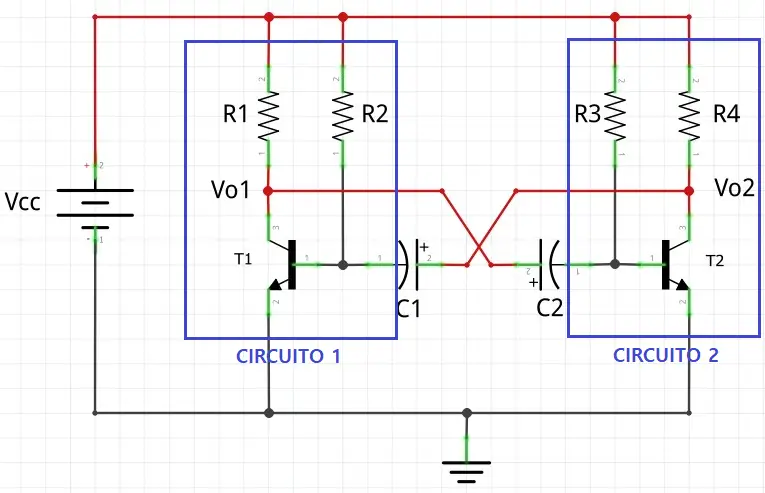
O circuito pode ser encontrado com diferentes arranjos (com capacitor sem polaridade ou com a polaridade invertida), mas a essência do funcionamento é a mesma. Entretanto, pretendo focar a explicação no circuito da imagem anterior.
Repare que as partes demarcadas em azul mostram os dois circuitos de polarização que comentei (polarização de base). E a interligação entre os circuitos é feita adicionando um capacitor eletrolítico na base de cada um e ligando no coletor do transistor oposto.
Observe também que o negativo do capacitor fica voltado para a base do transistor (isto será importante para o funcionamento).
Vo1 e Vo2 são as tensões entre o coletor do transistor e o terra (GND). São nestes pontos que os sinais de onda quadrada são gerados. Ele é gerado tanto em Vo1 quanto em Vo2. A diferença entre os dois é que, enquanto Vo1 está alta, Vo2 está em baixa e vice-versa. Portanto, os sinais são defasados em 180º (meio período).
Como calcular parâmetros
O cálculo dos resistores do multivibrador astável apresentado é feito a partir de um ponto de operação desejado do BJT. Isto é, basta você definir uma corrente de coletor para sua carga e calcular IB e os valores dos resistores com base no β do transistor.
Obs: O β do transistor pode ser encontrado em seu datasheet e, em alguns casos, ele é chamado de hFE (FE maiúsculo, pois hfe é outro tipo de parâmetro). Normalmente, o datasheet fornece uma faixa de valores e você pode utilizar o valor mínimo da faixa para o cálculo.
O post sobre como usar o BJT explica como são feitos os cálculos. E os cálculos são simples, pois é um circuito de polarização de base.
Agora, para calcular o valor do capacitor com base na frequência desejada do seu sinal, você deve utilizar a seguinte fórmula aproximada:
C = \frac{1}{2 \times ln(2) \times R_B \times f}
Onde f é a frequência do sinal de saída, C é o valor do capacitor e RB é o valor do resistor de base.
A expressão acima considera que o circuito é simétrico, isto é, R1 = R4, R2 = R3 e C1 = C2. Sendo assim, o sinal de saída também será simétrico: o tempo em alta é igual ao tempo em baixa.
Imagine agora que você deseja tirar a simetria da onda e, por exemplo, fazer o tempo em alta ser 90% do período e o tempo em baixa ser 10%. Para isso, cada capacitor é calculado separadamente. E o cálculo de um dos capacitores é feito utilizando a seguinte fórmula:
C = \frac{t_A}{ln(2) \times R_B \times f}
Onde tA é a fração do tempo em alta que você deseja (0,9 = 90%).
Para calcular o outro capacitor, utilize a mesma fórmula acima, mas, no lugar de tA, considere a fração do tempo em baixa (1-tA; 1-0,9 = 0,1).
A partir disto, você terá em Vo1 (ou Vo2) uma onda que fica 90% do período em alta e 10% em baixa. E, na outra saída, acontecerá o contrário: a onda ficará 90% do período em baixa e 10% em alta. Isso, porque uma saída é o inverso da outra.
Funcionamento do multivibrador astável
Neste primeiro momento, pretendo explicar a teoria do circuito para depois recorrer à simulação e mostrar como são as formas de onda de verdade.
Considerações iniciais
Antes de começar a analisar o comportamento do circuito, é importante fazer algumas considerações inicias para facilitar o entendimento. Primeiro, vou usar como base o circuito tipico mostrado anteriormente:
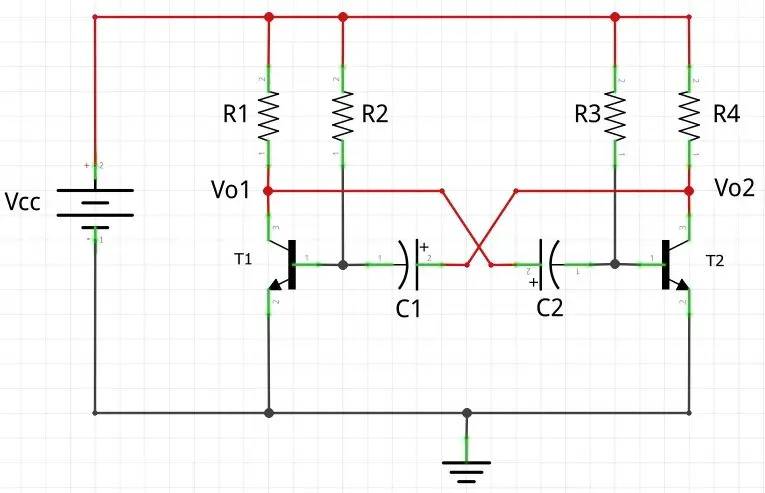
Vou considerar que o circuito é simétrico: R1 = R4; R2 = R3; T1 = T2 e C1 = C2. Conforme discutido anteriormente, isto produzirá uma onda simétrica na saída, pois os tempos envolvidos no circuito serão simétricos.
Além disto, farei a análise do funcionamento do circuito em regime permanente t>>0. Isto facilitará o entendimento do circuito. Entretanto, depois de analisar seu comportamento, voltaremos para falar sobre o regime transitório do circuito.
Instante 1 – Descarga de C2
Considere o capacitor C1 inicialmente descarregado e C2 carregado. A partir disto, a situação inicial do circuito está mostrada abaixo.
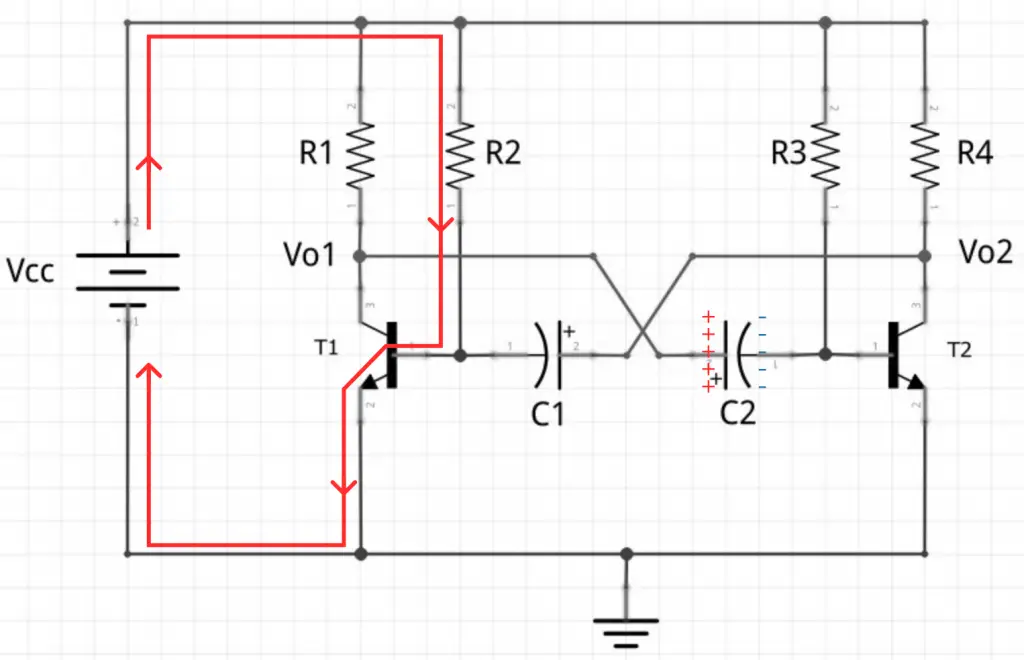
O transistor T1 começa a saturar (praticamente instantaneamente) devido à corrente que passa por R2. Enquanto isto, o capacitor C2 descarrega as suas placas de duas formas diferentes:
1 – A sua placa esquerda (positiva) é descarregada por meio do coletor do transistor T1. Repare que, quando o transistor 1 satura, a tensão Vce = Vcesat ~= 0V. Portanto, a placa esquerda de C2 tem um caminho livre (idealmente sem resistência) para descarregar. Por ser sem resistência, a descarga é imediata.
2 – A sua placa direita (negativa) começa a descarregar por meio de R3. Como o potencial na placa direita é negativo, o transistor T2 fica impedido de conduzir. Sendo assim, o único caminho possível para a placa direita descarregar é em R3.
Este processo está ilustrado abaixo:
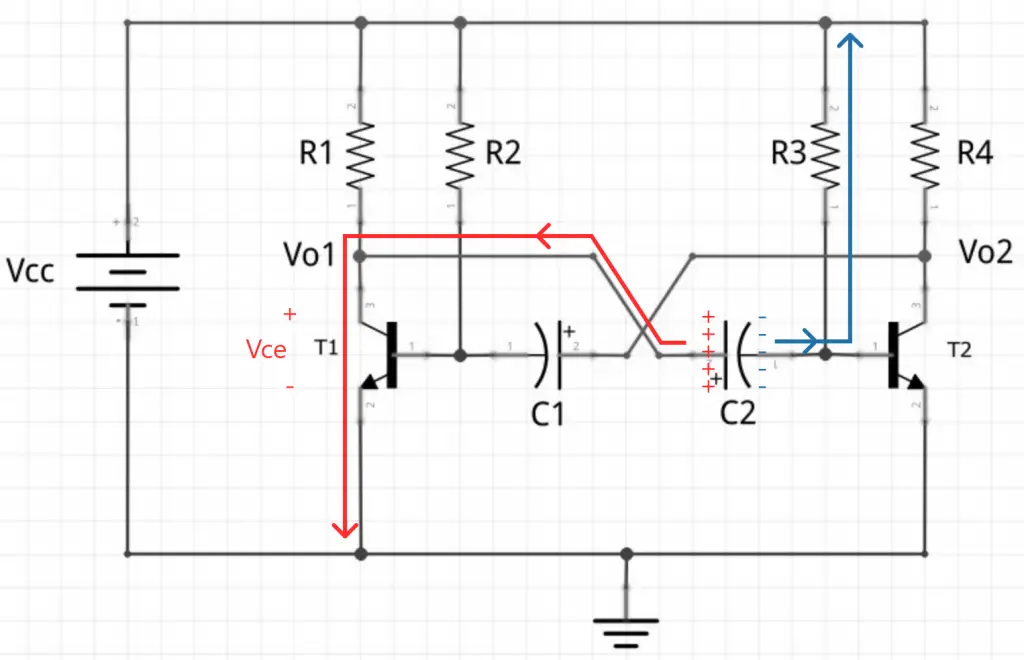
Com isto, o transistor T2 fica impedido de saturar até que a tensão em sua base fique positiva para que circule uma corrente ali suficiente para conduzir o transistor.
O tempo de descarga da placa negativa de C2 é dado pela fórmula aproximada:
T_{des} = ln(2) \times R_B \times C
Onde Tdes é o tempo de descarga, RB é o valor do resistor de base (R3) e C é o valor do capacitor.
Ou seja, o tempo de descarga é limitado apenas pelo valor do capacitor e do resistor de BASE.
Instante 1 – Carga de C1
Ao mesmo tempo que C2 descarrega, o capacitor C1 é carregado por meio da base do transistor T1 e resistor R4. Como T1 está saturado, a tensão em sua base é Vbe ~= 0,7V. E, como T2 está cortado, a tensão em Vo2 é próxima de Vcc. Sendo assim, C1 irá carregar com uma tensão próxima de Vcc.
A figura abaixo mostra o caminho da corrente para carregar C1.
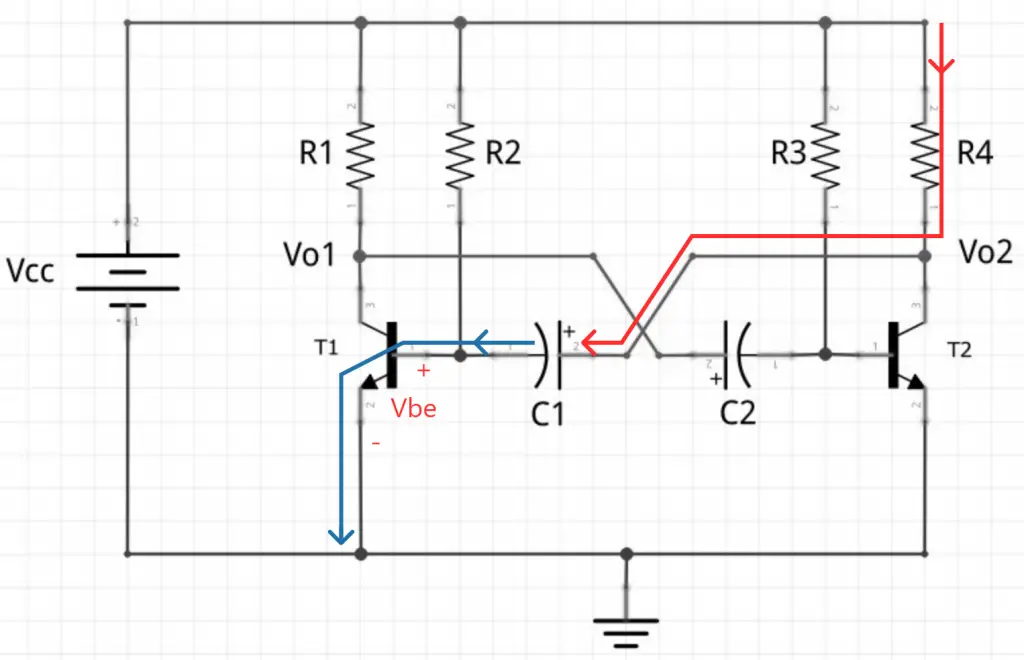
Observe que o tempo de carregamento de C1 é limitado pela resistência R4 e por resistências internas do transistor (que vamos desconsiderar neste contexto).
Normalmente, o valor de RB é muito maior que o valor de RC (podendo ser mais que 300 vezes maior). Por conta disto, o tempo de carregamento de C1 é consideravelmente menor que o tempo de descarga da placa direita de C2.
Relembrando, C2 descarrega por meio de R2 (RB) e C1 carrega por meio de R4 (RC). Logo, quando C2 terminar de descarregar, C1 já estará carregado.
Instante 1 – Saída Vo1 e Vo2
Sabemos que, neste primeiro instante, o transistor T1 satura e o transistor T2 fica impedido de saturar devido à tensão negativa gerada por C2.
Levando isto em conta, a tensão Vo1 será próxima de 0, pois, conforme disse, Vo1 = Vce ~= 0.
E a tensão Vo2 será próxima de Vcc, pois o transistor T2 está cortado. Aqui é importante observar um detalhe muito importante:
Vo2 está ligado à placa direita do capacitor C1. Sendo assim, a tensão Vo2 não será imediatamente Vcc, a tensão será uma curva logarítmica crescente, pois acompanhará o carregamento de C1. A tensão Vo2 e a tensão na placa direita do capacitor C2 terão comportamento igual às curvas azul e verde, respectivamente, do gráfico abaixo.
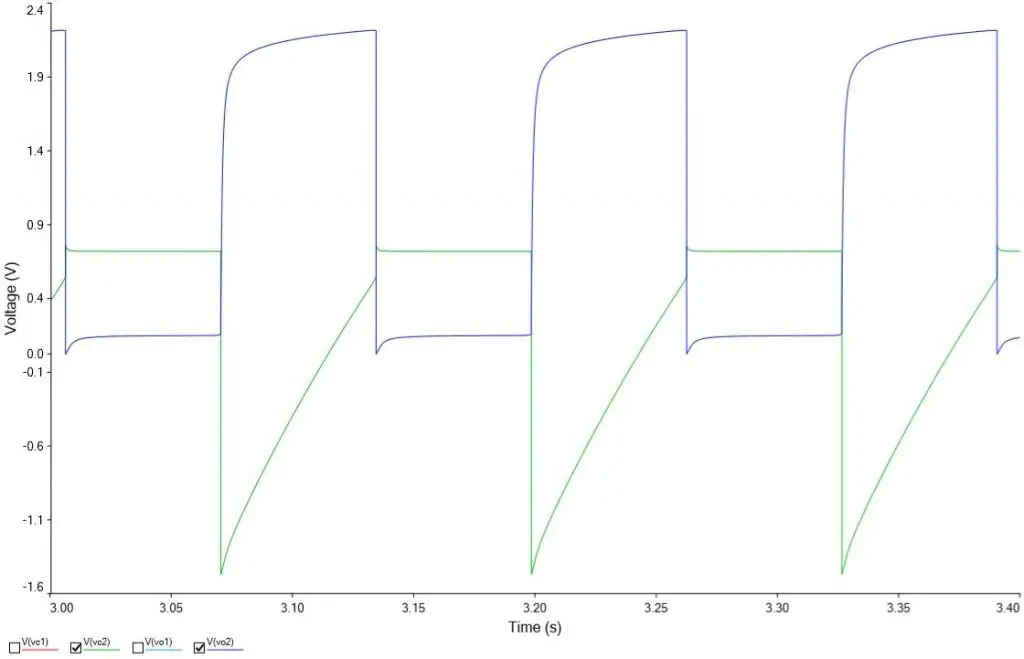
O gráfico acima será melhor detalhado no tópico da simulação.
Instante 2 – Inversão dos estados
Quando o instante 1 chegar próximo do fim, teremos os seguintes estados: T1 saturado, T2 em corte, C1 carregado e C2 descarregado.
O instante 1 chega ao fim quando C2 descarrega a tal ponto que a tensão na base de T2 é suficiente para polarizar T2. Neste momento, T2 começa a saturar.
Obs: Na realidade C2 descarrega até 0 volts e depois carrega minimamente até ter uma tensão próxima de Vbe.
Com a saturação de T2, o capacitor C1 começa a descarregar assim como C2 no instante 1:
A placa direita (positiva) de C1 descarrega por meio do coletor de T2 e a placa esquerda (negativa) começa a descarregar por meio de R2 (RB). Com isto, a tensão na base de T1 fica negativa e T1, que antes estava saturado, começa a ficar cortado.
A partir do que foi descrito acima, é perceptível que o comportamento do circuito está se repetindo, porém de forma invertida. E de fato está mesmo:
O capacitor C2 irá carregar por meio de R1 (RC). E este carregamento será mais rápido do que o descarregamento de C1, pois R1 (RC) é consideravelmente menor que R2 (RB).
Instante 2 – Saída Vo1 e Vo2
Como T1 passou a ficar cortado e T2 saturou, as saídas Vo1 e Vo2 foram invertidas. Isto é, Vo1 agora é próximo de Vcc e Vo2 é próximo de 0 (Vcesat).
Com isto, é possível perceber como este circuito é capaz de gerar o sinal de onda quadrada. Já que, a cada instante, um dos transistores está conduzindo enquanto o outro está cortado.
E a defasagem de 180º entre Vo1 e Vo2 que comentei no início do post se dá por conta desta oposição de estados entre T1 e T2.
Observação
Se você chegou até aqui, deve ter entendido que o tempo entre cada troca de estado de Vo1 ou Vo2 é dado pelo descarregamento de C1 ou C2. E o descarregamento de ambos é dado pela aproximação (conforme dito):
T_{des} = ln(2) \times R_B \times C
Se Tdes é o tempo entre cada comutação, quer dizer que Tdes se refere à metade do período do sinal gerado (Tdes = T/2). A partir disto, você deve ser capaz de saber de onde veio a fórmula do cálculo do capacitor.
Simulação
Circuito
Para mostrar as formas de onda do circuito na simulação, pretendo utilizar o circuito mostrado na figura abaixo.
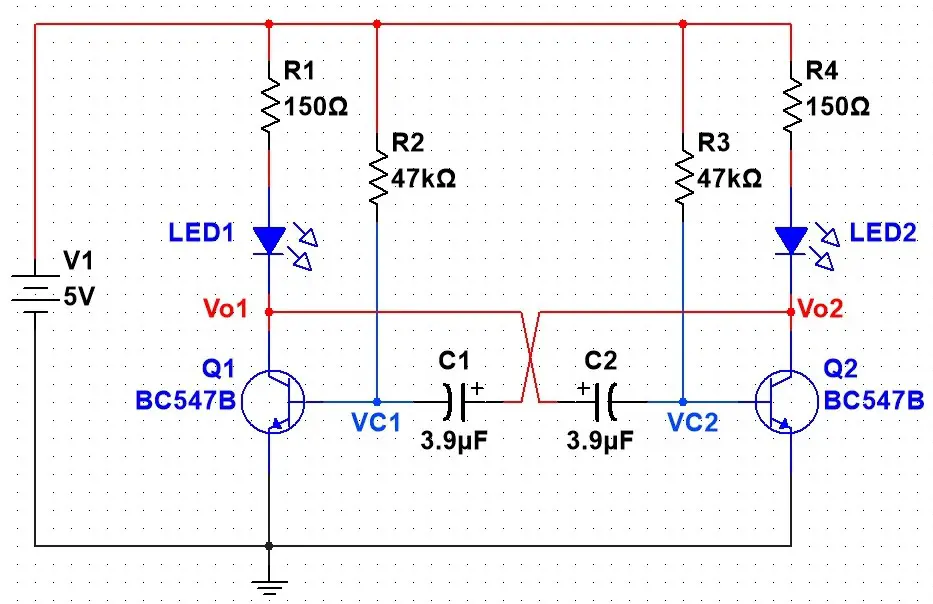
Este circuito é o mesmo mostrado anteriormente, porém com a adição de LEDs em série com o coletor do transistor. Os LEDs servem para ter uma resposta visual da forma de onda gerada pelo circuito.
Os valores dos resistores foram calculados para uma polarização considerando: Ic = 20mA; β = 219 (encontrado na prática para o BJT BC547B). E os capacitores foram calculados usando a fórmula apresentada anteriormente considerando uma frequência de 4Hz.
O comportamento do circuito será o mesmo de antes, porém o LED irá acender quando o transistor saturar e irá apagar quando este estiver cortado. De qualquer forma, se você montar o circuito na prática, verá os LEDs acendendo de forma alternada (um acende o outro apaga e vice-versa) em uma frequência próxima de 4Hz.
Obs.: A simulação será feita depois dos 3s de funcionamento para pegar o regime permanente do circuito.
Sinal de Vo2 e VC2
Relembrando o instante 1 do tópico anterior: enquanto C2 descarrega, T2 fica cortado e, portanto, Vo2 é próximo de Vcc.
O gráfico seguinte mostra a tensão Vo2 (em azul) e a tensão VC2 na placa direita (negativa) de C2 (em verde).

O gráfico está praticamente de acordo com o esperado e podemos extrair detalhes bem interessantes dele:
1 – VC2 é negativo e aumenta gradualmente até ser minimamente positivo ao ponto que T2 começa a saturar. No fim deste processo é possível reparar que VC2 da um salto de de ~0,5V para ~0,7.
Isto ocorre, porque, em ~0,5V, T2 satura e a tensão na base do transistor passa a ser a tensão Vbe que é próxima de 0,7V. A mudança é praticamente imediata, pois não há, idealmente, nenhuma resistência para atrasar o carregamento da placa direita do capacitor.
2 – A amplitude de Vo2 está bem longe de Vcc. O que acontece é que, neste circuito com os LEDs, tanto C1 quanto C2 irão carregar com a tensão que chega em Vo. E, a tensão que chega em Vo é Vcc menos a queda de tensão do LED (que é próxima de 2,5V).
O terceiro item será comentado abaixo.
Vo2 e tempo de carga de C1
Conforme foi mencionado anteriormente, quando T2 fica cortado, a tensão Vo2 não sobe imediatamente para o seu valor máximo. Relembrando: isto se dá devido ao carregamento de C1, pois ele está ligado em Vo2. E este tempo de atraso (ta) pode ser aproximado pela expressão:
ta = 5*τ = 5*RC*C
Que, para o caso do circuito vale:
ta = 5*150*3,3μ = 2,93mS
Com a imagem abaixo, podemos verificar isso. Ela mostra Vo1, mas o sinal de Vo1 é praticamente igual ao de Vo2:
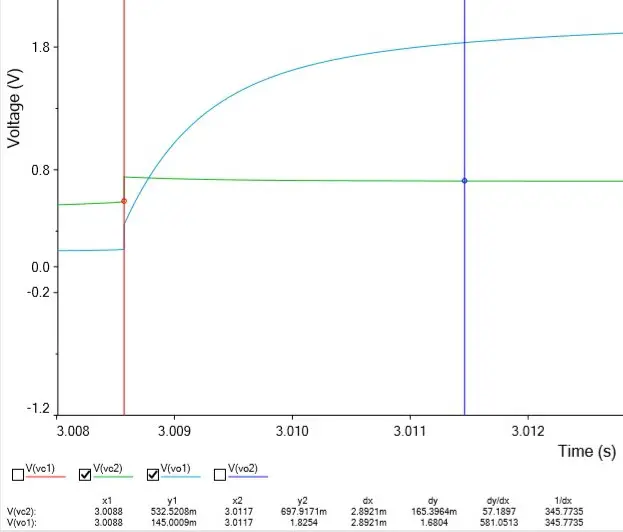
Os cursores estão definidos no início da curva e em um ponto em que a tensão já é próxima da máxima. Na parte inferior do gráfico, estão exibidas as informações dos cursores. E o Δt entre os dois é 2,8921mS. Ou seja, está próximo do esperado (2,93mS).
Sinal de Vo1 e VC1
Para Vo1 e a tensão na placa negativa de C1 (VC1), podemos verificar o mesmo comportamento anterior. Veja o sinal de ambos abaixo:
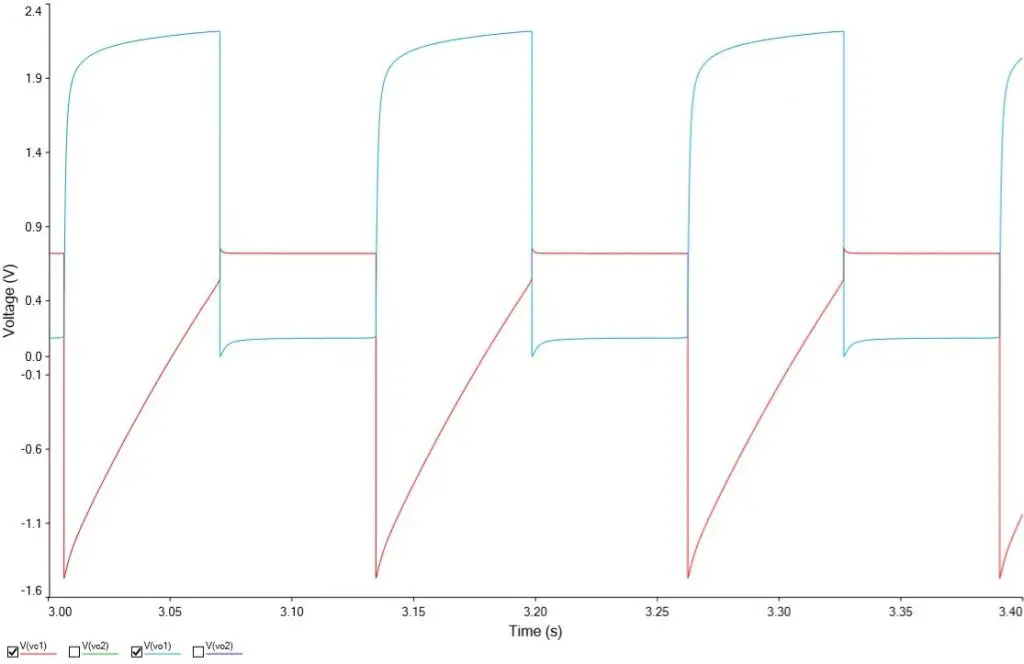
Os comentários anteriores são igualmente válidos para este gráfico.
Sinais de saída e dos capacitores
Por fim, se juntarmos os sinais no mesmo gráfico, obteremos o seguinte:
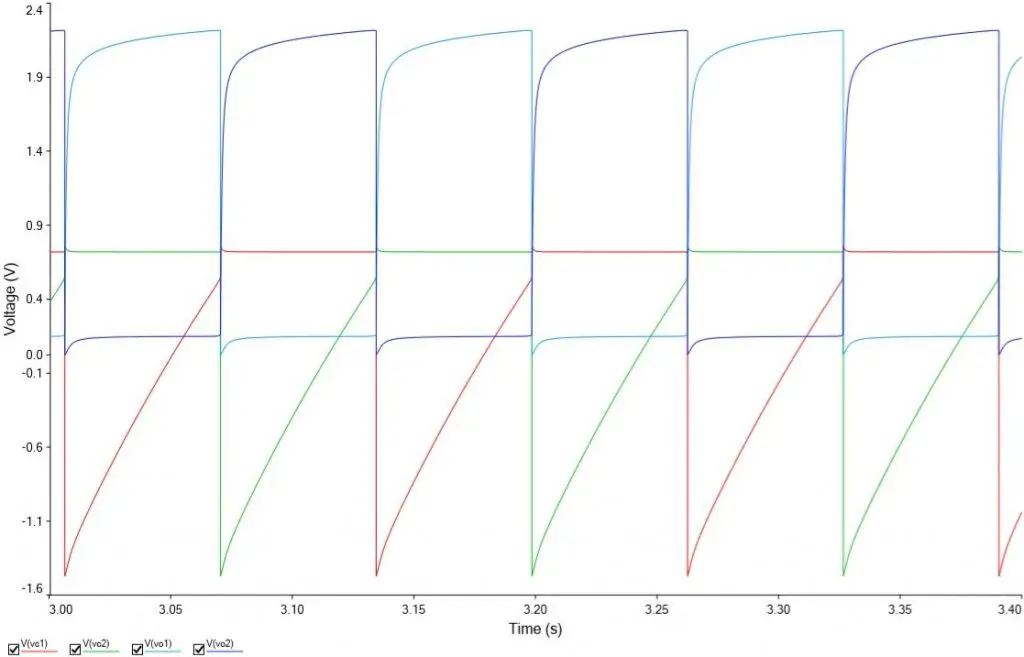
Aqui, é possível perceber a defasagem de 180º entre a onda quadrada gerada por Vo1 e a gerada por Vo2.
Um último detalhe importante é a frequência do sinal de saída. Assim como mencionei no tópico de circuito, a frequência calculada é cerca de 4Hz. Entretanto, quando medi, ela foi cerca de 8Hz, quase o dobro da calculada.
Este erro se deve à aproximação grosseira que a fórmula faz para o caso de utilizar os LEDs. Isto porque o desenvolvimento da fórmula não considera a queda de tensão dos LEDs. De qualquer forma, se você não utilizar os LEDs, o resultado final deve ser bem satisfatório.
Tanto é que, sem os LEDs, a frequência medida foi cerca de 4,5Hz (um erro bem menor desta vez).
Observações finais
Regime transitório
Agora que já entendemos como o multivibrador astável funciona em regime permanente, podemos analisar como ele sai do transitório.
O primordial desta primeira etapa é que um capacitor começa a carregar primeiro que o outro e um transistor começa a saturar primeiro que o outro. No mundo real, isto é fácil de aceitar, já que componentes supostamente idênticos possuem diferenças pequenas, que já são suficientes para este efeito.
E este fato desencadeia os efeitos que vimos anteriormente. De qualquer forma, vamos olhar como são os sinais na simulação no instante em que o circuito é energizado:
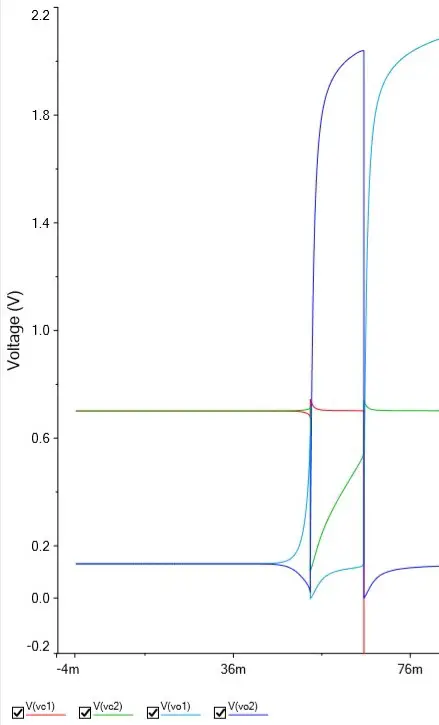
Apesar de não dar para ver direito, tanto VC1 quanto VC2 estavam em ~0,7V (Vbe). E ambos os transistores estão saturados.
Entretanto, de repente, o transistor T1 começa a cortar e T2 satura mais ainda. O fato de T1 começar a saturar faz com que C2 seja carregado parcialmente. E, na sequência, C2 começa a descarregar impedindo que T2 seja saturado.
Se T2 está cortado, T1 está livre para saturar enquanto C1 é carregado. É o mesmo processo de antes, porém em um tempo mais rápido. Porque, como C2 foi carregado parcialmente, sua descarga é mais rápida.
Por fim, assim que C2 termina de descarregar, o multivibrador astável entra em seu pleno funcionamento e se comporta de acordo com o que estudamos.
Aplicações do multivibrador astável
O multivibrador astável pode ser utilizado nas seguintes situações:
- Gerar o clock de circuitos digitais.
- Gerar um PWM por meio da adição de um capacitor variável no circuito.
- Geradores de código Morse.
- Equipamentos de rádio amador.
- Sinalizador de entrada/saída de veículos em garagens.
CI 555 – O que é e como funciona

Ótimo conteúdo!
Obrigado pela postagem.
Eu é que agradeço pelo comentário, Edmundo!
Nas considerações iniciais, se o circuito é simétrico, o correto seria R1=R4 e R2=R3.
Este comentário pode ser excluído livremente após a correção.
Parabéns pelo conteúdo! Primeiro lugar que eu acho a explicação sobre a dinâmica do circuito e os transientes.
Olá, Alexandre. Muitíssimo obrigado pelo comentário! Este erro acabou passando despercebido. Fiz a correção e aproveitei para arrumar a formatação do post. Espero que os demais assuntos do site também sejam uteis para você!
Excelente conteúdo, Fabio. Fiquei admirado com sua didática através do post. Realmente, somos nós que agradecemos.
Só uma obs.: Você pode explicar de onde veio o ln2 na fórmula do capacitor, por favor. Desconfio que seja do tempo de carga do capacitor (Vc = Vcc * (1 + e^(-t/RC)) mas gostaria da sua explicação =)
E também, poderia acrescentar no post: Pra quem não conseguir descobrir o valor do Beta do seu transistor, pode ir no datasheet, ver o valor do hFe mínimo e dividir por 2, ai teremos o valor de hFe de saturação. Icsaturação = hFesaturação * Ibsaturação. E depois continua os cálculos normais. Já que se trata de apenas cortar e saturar os transistores. No mais, muito legal seu post. Vaaaaleu por compartilhar o conhecimento tão explicadinho
Olá, Matheus. Hehe sem problemas! Obrigado pelo comentário, fico feliz que tenha gostado.
Na época que escrevi este post, eu não fazia ideia de onde veio esse ln(2), mas encontrei uma explicação nesta página da wikipedia.
Acontece que o período do multivibrador astável é definido pelo descarregamento dos capacitores, pois, conforme dito, ele é mais lento que o carregamento. E usamos uma fórmula mais genérica que mostra qual é a tensão do capacitor para certas condições: Vc(t) = (Vcinicial – Valimentação)*e^(-t/RC) + Valimentação
Se considerarmos que Valimentação = Vcc e Vcinicial = -Vcc (no momento da descarga a tensão do capacitor é negativa), então:
Vc(t) = (-Vcc – Vcc)e^(-t/RC) + Vcc -> Vc(t) = Vcc [1 – 2e^(-t/RC)]
A comutação dos transistores ocorre quando a tensão do capacitor que está descarregando fica praticamente igual a Vbe (tensão mínima para polarizar a base do transistor). Então, se Vc(t) = Vbe:
Vbe = Vcc [1 – 2e^(-t/RC)]
Por meio de um algebrismo, conseguimos obter a equação em função de t:
Vbe/Vcc = 1 – 2e^(-t/RC) -> 2e^(-t/RC) = 1 – Vbe/Vcc -> e^(-t/RC) = (1 – Vbe/Vcc)/2
Vou fazer uma consideração aqui já de uma vez pra não ficar confuso adiante. Para chegar ao ln(2), considera-se que Vcc é muito maior que Vbe, então a conta Vbe/Vcc tende a 0:
e^(-t/RC) = (1 – 0)/2 = 1/2
Continuando o algebrismo, aplica-se ln nos dois lados da equação:
-t/RC = ln(1/2) -> t/RC = -ln(1/2)
A partir das propriedades de logaritmo:
-ln(1/2) = ln(1/2 ^ -1) = ln(2)
Então:
t = ln(2) * R * C
Espero que tenha dado para entender. Obrigado pela sugestão sobre o valor do Beta. Estas últimas semanas estou agarrado com faculdade, mas, assim que possível, vou corrigir uns erros que achei e acrescentar o detalhe que você comentou.
Eu não entendi o que é o Ln(2) na fórmula.
Pergunto se seria a constante de tempo de carga máxima de 69% da tensão aplicada sobre o capacitor ?
Olá, Thiago. Não é não, na verdade é algo mais complicado. Na época decidi não colocar no post, pois achei que ia ficar muito cheio de informação. Mas, você pode entender de onde vem o Ln(2) lendo o tópico “Multivibrator frequency” dessa página da wikipedia. Resumo: O Ln(2) sai de uma série de manipulações e simplificações feitas na fórmula genérica da tensão em cima de um capacitor ao longo do tempo Vcap(t). É um pouquinho demorado pra entender, mas é bem interessante.
Eu ainda não tinha entendido muito bem, mas com um tanto mais de pesquisa deu pra compreender que Ln(2) significa “logarítimo natural do número 2”. Até sei o que é uma escala logarítmica, mas ainda não entendo o porque ela entra nos cálculos do oscilador. De qualquer firma continuarei estudando.
Agradeço pelo esclarecimento.
Poxa, Thiago. Pelo visto eu não tinha entendido exatamente sua dúvida inicial, foi mal. Mas o Ln(2) é exatamente o que você falou mesmo. Ele surge ao manipular a equação (da wikipedia) para transformar ela de Vc(t) em t(Vc). Isto é, você quer isolar a variável t na equação. E, se você reparar bem, a variável t aparece no expoente do número de Euler (a letra e). O que é feito para isolar uma variável que está elevada a um expoente é aplicar o logaritmo nos dois lados da equação. Nesse caso, aplica-se o logaritmo natural, que é um logaritmo que possui o número de Euler em sua base (Ln(x) = Log(x) na base e). Assim, quando você aplica Ln na equação, em algum momento (após usar as propriedades de logaritmo), você sairá com um termo Ln(2). Detalhe: falei que o objetivo é isolar a variável t, mas no post coloquei a equação em função da frequência. Aí vale lembrar que t = 1/f ou f = 1/t.
Olá Fábio Guimarães, muito bem, muito bom todo o conteúdo do Mundo Projetado. Melhor ainda as ilustrações, que suponho tenham sido obtidas, por um aplicativo(sotware) de simulação de circuitos; gostaria que informa-se qual programa você usa?! Ficaram ótimas as simulações que com tuas ilustrações fizeram um grande conjunto. Parabéns novamente
Olá, Newton. Muitíssimo obrigado pelo comentário! Fico feliz com esse retorno.
Acabei usando 3 programas diferentes para criar as imagens deste post:
Fritzing para o desenho do circuito, exceto o circuito do tópico “Simulação”;
Figma para desenhar as setas e textos em cima da imagem do circuito;
Multisim para simular e desenhar o circuito do tópico “Simulação”.
Não lembro ao certo por quê não usei Multisim para desenhar todos os circuitos.