O multiplexador e o demultiplexador são bastante utilizados em circuitos de telecomunicações. Então, é interessante aprender o que são e como funcionam.
Na aula anterior, estudamos os codificadores e os decodificadores.
Informações básicas
A ideia por trás do multiplexador e do demultiplexador é semelhante ao que foi abordado na aula passada. Eles nada mais são do que circuitos que utilizam portas lógicas para criar certas funções. E são considerados como circuitos de média complexidade.
Como o foco deste curso é a Eletrônica Digital, iremos abordar o multiplexador e o demultiplexador digital, embora exista também o analógico. Adiante entenderemos este ponto e a diferença entre eles será explicada.
Multiplexador
Conceito
O multiplexador, ou simplesmente MUX, é um circuito que possui diversas entradas e uma única saída. E ele é capaz de selecionar qual entrada será ligada na saída, sendo que só uma é ligada por vez. Por conta disto, existem entradas de “controle” que servem para fazer esta seleção.
O MUX é útil em casos em que você só tem um fio/canal e diversos dispositivos precisando de utilizar este canal. Desta forma, é possível selecionar qual dispositivo utilizará o canal em cada momento sem um atrapalhar o outro.
Exemplo de multiplexador
Para exemplificar o funcionamento do MUX, vou utilizar um MUX de 4 entradas. Como consequência, são necessárias 2 entradas de controle para selecionar qual entrada será ligada à saída. Veja a imagem abaixo:
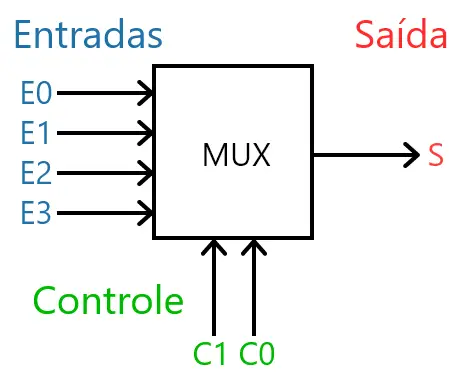
De acordo com o valor de C1 e C0, alguma entrada (E0 – E3) é ligada diretamente à saída (S) enquanto as outras entradas ficam desconectadas.
A tabela-verdade deste MUX pode ser representada como:
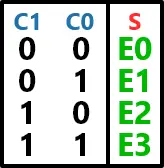
Quando C1 e C0 estiverem em nível baixo, o valor da saída S será igual ao valor da entrada E0. Isto é, se E0 estiver em alta, S estará em alta e vice-versa. Esta mesma lógica é aplicada aos demais estados de C1 e C0, que sempre selecionam uma respectiva entrada para ligar à saída.
Construindo um multiplexador
Um MUX nada mais é do que um arranjo de portas AND, cada uma ligada a uma entrada específica, e todas ligadas às entradas de controle. Além das portas AND, há também uma porta OR para interligar as saídas das portas AND.
Veja o circuito abaixo que modela o MUX de 4 entradas apresentado no tópico anterior:
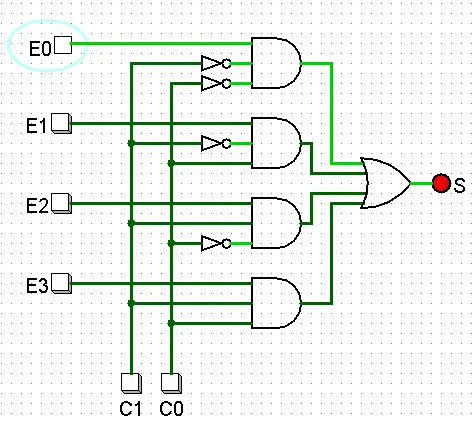
Na imagem acima, C0 e C1 estão em baixa, selecionando a entrada E0. E E0 está em alta, com isto, S também fica em alta.
É possível perceber que, no circuito acima, cada AND está associada a um estado das entradas de controle. A primeira AND (de cima para baixo) precisa ser acionada com C0 e C1 em baixa (00), a segunda com C0 em alta e C1 em baixa (01) e assim em diante…
Além das entradas de controle, sobram as entradas (E0-E3) nas ANDs. Por exemplo a 4ª AND: se C0 e C1 forem 1, a saída dependerá apenas do valor de E3. Se E3 estiver em baixa, a saída será 0 e se estiver em alta, a saída será 1.
Demultiplexador
Conceito
O demultiplexador, ou simplesmente DEMUX, como o próprio nome sugere, é o circuito inverso do MUX:
Ele possui uma só entrada e várias saídas. E ele é capaz de selecionar qual saída será ligada na entrada, sendo que só uma saída é ligada por vez.
Novamente, aqui também vão existir as entradas de controle que, neste caso, servem para fazer a seleção das saídas.
O DEMUX possui a mesma aplicação anterior: casos em que você só tem um fio/canal e diversos dispositivos precisando de utilizar este canal. Porém, no caso do DEMUX, ele será utilizado na outra ponta do canal, selecionando para qual dispositivo o sinal de entrada será direcionado.
Exemplo de demultiplexador
Para exemplificar o funcionamento do DEMUX, vou considerar um DEMUX de 4 saídas. Assim como antes, existirão 2 entradas de controle. Veja a imagem abaixo:
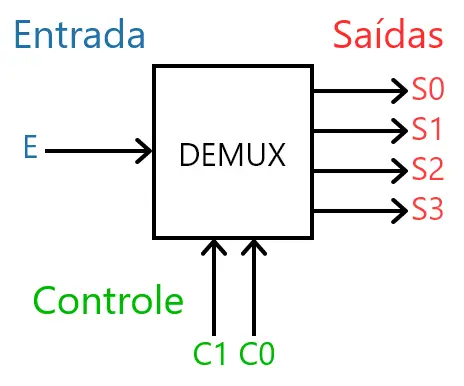
De acordo com o valor de C1 e C0, alguma saída (S0 – S3) é ligada diretamente à entrada (E) enquanto as outras saídas ficam desconectadas (em nível lógico baixo).
A tabela-verdade deste DEMUX pode ser representada como:
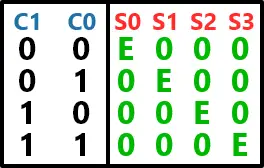
Quando C1 e C0 estiverem em nível baixo, o valor da saída S0 será igual ao valor da entrada. Isto é, se E estiver em alta, S0 estará em alta e vice-versa. Esta mesma lógica é aplicada aos demais estados de C1 e C0, que sempre selecionam uma respectiva saída para ligar à entrada.
Construindo um demultiplexador
O circuito de um DEMUX é praticamente igual ao de um MUX, com a diferença que o DEMUX não utiliza uma OR para interligar as ANDs. Isso porque a saída de cada AND é ligada a um saída (S0-S3).
Veja o circuito abaixo que modela o DEMUX de 4 saídas apresentado no tópico anterior:
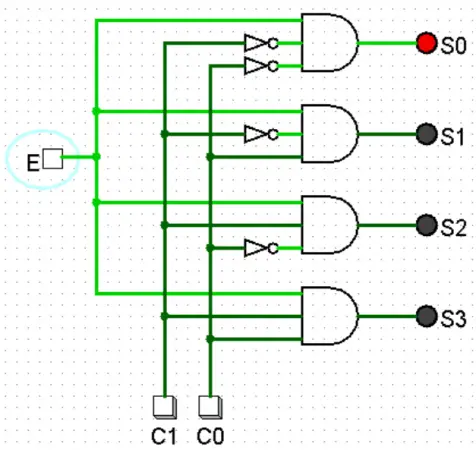
Na imagem acima, C0 e C1 estão em baixa, selecionando a saída S0. E a entrada E está em alta, com isto, S0 também fica em alta.
Novamente, cada AND está associada a um estado das entradas de controle…
Por exemplo, a 4ª AND: se C0 e C1 forem 1, a saída S3 dependerá do valor de E3 enquanto as outras ficarão em nível baixo.
Observações finais
Simbologia
Ao longo do post, eu mostrei os símbolos do MUX e do DEMUX como sendo um retângulo, entretanto eles são usualmente representados em um formato trapezoidal igual ao da imagem abaixo:
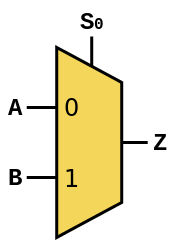
O símbolo acima é apenas do MUX, mas o do DEMUX é análogo a ele (veja próximo tópico).
Ligação entre MUX e DEMUX
Recapitulando a aplicação que foi mencionada sobre transmitir várias informações em um mesmo fio/canal, agora podemos entender melhor como o MUX se interliga com o DEMUX.
Veja a imagem abaixo:
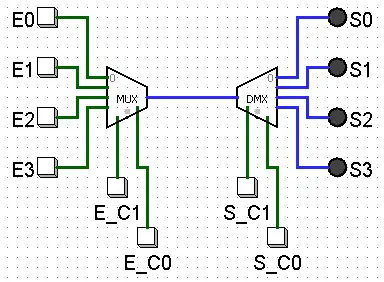
A ideia é que um dispositivo é selecionado para transmitir (E0-E3), com isto seu sinal é transferido da entrada do MUX para a saída. Seguindo esta sequência, na outra ponta do fio/canal, uma saída correspondente ao sinal do dispositivo que transmitiu é selecionada pelo DEMUX.
Sendo mais específico, imagine que seja um sistema de telefonia: de um lado temos várias casas de um certo bairro ligadas a uma central, e do outro lado casas de outro bairro ligadas também à central. Todas as casas compartilham o mesmo fio para falar no telefone, por isto é preciso multiplexar/demultiplexar os telefones um por vez para todos conseguirem utilizar o canal. E também, por meio deste esquema, os telefones da esquerda conseguem se comunicar com qualquer telefone da direita apenas mudando a seleção desejada.
Se mais de um telefone precisar ser utilizado por vez é possível ir mandando os dados de voz de forma rápida e intercalada. Ou seja, durante um instante pequeno, o telefone E0 manda e, durante outro instante pequeno, o telefone E1 manda. Mas isto é só uma ideia de como o sistema de telefonia funciona. Na realidade ele é bem mais complexo que isto.
MUX e DEMUX digital x analógico
O MUX e o DEMUX apresentados nesta aula são digitais, o que quer dizer que o sinal de saída nos dois casos é apenas 0 ou 1.
Caso fosse necessário utilizar um MUX/DEMUX para escolher entre sinais analógicos (senoide por exemplo) seria necessário utilizar um MUX/DEMUX analógico.
O MUX/DEMUX analógico possui um circuito diferenciado do apresentado e se assemelha mais a uma chave seletora e não “digitaliza” o(s) sinal(is) de entrada.
Próximo assunto
O próximo passo será aprender sobre os circuito sequenciais, que são circuitos em que o estado da entrada depende de estados atuais e estados passados das entradas. Ou seja, é um circuito que pode variar no tempo.
Circuito digital sequencial (Latch) – Aula 9 – ED

Na seção Ligação entre Mux e Demux, o texto diz que “E também, por meio deste esquema, os telefones da esquerda conseguem se comunicar com qualquer telefone da direita apenas mudando a seleção desejada”.
Como o E0 se comunicaria com o S1, por exemplo?
Olá, Elizeu. Da forma como a ligação estava feita, realmente não tinha como fazer isto que você comentou. Só dava pro E0 falar com o S0, E1 com S1 e assim em diante. Fiz uma correção na imagem e veja se a ligação faz sentido agora.
Eu preciso entender como fazer a tabela de Verdade para um circuito Mux/Demux
Olá, poderia dar um exemplo do tipo de circuito que você quer montar? Pois, a princípio, dá pra seguir as tabelas-verdade mostradas no post.
como posso fazer um mapa de karnaugh de um multiplexador?
Excelente pergunta. A princípio seria da mesma forma que você faria para um outro circuito qualquer. A questão é que não é possível simplificar o circuito pois a mapa seria preenchido com as entradas (E0, E1, E2…) e não com 1s e 0s. A diferença é que cada minitermo (veja a aula sobre mapa de Karnaugh) seria “multiplicado” pela entrada correspondente. Exemplo, o minitermo da primeira linha e coluna seria (¬C0)(¬C1)E0 (C0 e C1 negados). Levando isso em conta, é mais fácil construir o circuito direto da tabela-verdade fazendo esse processo que comentei na frase anterior linha por linha da tabela.