Dando continuidade à criação de circuitos combinacionais, vamos estudar o mapa de Karnaugh que é muito útil na simplificação das expressões de saída.
Na aula anterior, aprendemos a criar um circuito combinacional de forma simples.
Informações básicas
Não deixe de ler o post da aula anterior para saber como criar uma tabela-verdade e entender o que são minitermos e maxitermos.
O que é o mapa de Karnaugh
O mapa de Karnaugh é um método para simplificar as expressões das saídas de circuitos combinacionais. Ele nada mais é do que uma espécie de diagrama (ou mapa, como diz o nome) que é montado para cada saída a partir de uma tabela-verdade.
Este mapa serve para gerar os minitermos mais simples de uma saída. Portanto, idealmente, a expressão de saída gerada será simplificada ao máximo e não terá redundâncias.
Adiante, nós veremos como ele é construído e como utilizá-lo.
Raciocínio por trás
Antes de ver como criar o mapa de Karnaugh, é importante entender a teoria de simplificação a qual ele recorre.
O mapa é criado de forma que haja variação de apenas uma variável entre duas condições consecutivas.
Se lembrarmos da tabela verdade, entre uma linha e outra (qualquer), há variação do estado de 1 ou mais entradas. E, o mapa de Karnaugh, “reorganiza” a tabela de forma que apenas uma entrada altere seu estado entre uma linha e outra. Esta “reorganização” é chamada de código Gray.
E, a vantagem de se fazer isto é poder contar com a seguinte simplificação da álgebra Booleana:
AB + A(¬B) = A(B + ¬B) = A
Isto é, entre a condição AB e a condição A(¬B), apenas uma entrada mudou de estado. Portanto, ao organizar a tabela-verdade com a lógica do código Gray, é possível fazer este tipo de simplificação quando uma mesma saída em duas linhas consecutivas for 1.
Obs: O mapa de Karnaugh não é uma tabela-verdade reorganizada, ele só aproveita a lógica do código Gray para criar o mapa. Entenderemos isto a seguir.
Como criar o mapa de Karnaugh
Para criar o mapa de Karnaugh, precisamos de ter a tabela-verdade do circuito pronta. Desta forma, para exemplificar, vou utilizar a seguinte tabela verdade (valores aleatórios):
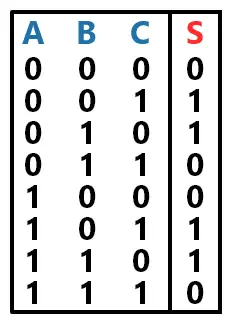
O mapa será feito para a saída S, já que ela é a única saída da tabela. Mas, se houvessem outras, seria necessário criar um mapa para cada saída.
O procedimento que mostrarei adiante não é a única forma de criar o mapa, embora seja a mais simples.
1º passo – Agrupando as entradas
Agrupe as entradas em dois grupos, preferencialmente na ordem do bit mais significativo para o menos significativo. Não tem problema se os grupos não tiverem a mesma quantidade de entradas. O importante é não deixar um grupo vazio. Por exemplo, um grupo poderia ter 10 entradas e o outro apenas 1.
Sendo assim, para a tabela-verdade anterior, poderíamos ter as possibilidades (mais usuais):
- Grupo 1: AB. Grupo 2: C
- Grupo 1: A. Grupo 2: BC.
Para seguir com o exemplo, vou adotar a primeira possibilidade (AB e C).
2º passo – Criando tabela
Crie uma tabela quadriculada com x linhas e y colunas. Sendo que:
- As linhas se referem às entradas do grupo 1, e as colunas às entradas do grupo 2.
- x será igual à 2^n, sendo n o número de entradas do grupo 1.
- y será igual à 2^n, sendo n o número de entradas do grupo 2.
No fim das contas, a multiplicação de x por y tem que ser igual à quantidade de linhas da tabela-verdade. E esta, por sua vez, é igual a 2^n, sendo n o número total de entradas.
De acordo com o exemplo que estamos usando: O grupo 1 tem duas entradas (A e B), portanto x = 4; o grupo 2 tem 1 entrada, logo y = 2. Com isto, terei que criar uma tabela quadriculada 4×2 (linhas x colunas), conforme imagem abaixo:
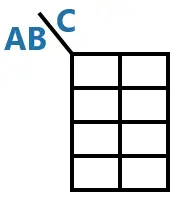
Na tabela acima, já realizei outra etapa importante que não mencionei: escrever os grupos no topo da tabela separados por uma barra. Isto ajuda a visualizar a quais entradas as linhas/colunas se referem.
No exemplo acima, sabemos que as linhas dizem respeito às variáveis A e B e as colunas dizem respeito à variável C.
3º passo – Estado das entradas
Ao lado de cada linha e acima de cada coluna, escrever o estado das entradas referentes àquela linha/coluna. Esta escrita segue a ordem do código Gray, que é:
0, 1, 11, 10…
Apenas os 4 primeiros valores da sequência são importantes para as aplicações mais básicas. Mas, caso você precise saber do resto, é só pesquisar quais são os demais valores.
No nosso exemplo, ao lado das linhas, teremos que escrever os diferentes estados de A e B. E, acima das colunas, serão os estados de C.
É comum escrever os bits de acordo com a ordem das entradas no grupo. Isto é, 1º bit: 1ª entrada do grupo; 2º bit: 2ª entrada do grupo; assim em diante. Veja a imagem abaixo para entender:
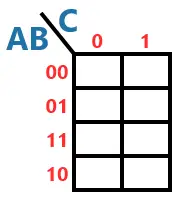
Os valores 00, 01, 11 e 10 são relativos às entradas A e B. E o 1º bit é relativo à entrada A e o 2º bit é relativo à entrada B. Como as colunas possuem apenas a entrada C, então existe apenas 1 bit e não há confusão.
4º passo – Estado da saída
Após o passo anterior, você já criou um mapa. Mapa este que cada linha e coluna diz respeito à uma condição do seu circuito. Pegando a imagem anterior como exemplo: a linha 1 e coluna 1 do mapa são referentes às condições do circuito quando A, B e C são 0.
Seguindo esta lógica, o 4º passo diz respeito a escrever o estado da saída para cada linha e coluna do mapa. Então, analise quadrado por quadrado e escreva 0 ou 1 de acordo com o estado da saída.
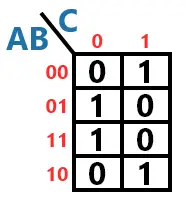
Na imagem acima, é possível perceber que, na primeira linha e segunda coluna, A e B são 0 e C é 1. Se você olhar na tabela-verdade, nesta condição a saída é 1. Por isto está escrito 1 neste quadrado.
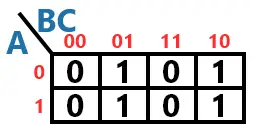
O preenchimento do mapa segue mais ou menos a ordem da tabela-verdade. O que muda é a 3ª e 4ª linha, pois é como se elas estivessem “trocadas”. Se o mapa fosse feito com o grupo (A e BC), ele seria 2×4 e o que “trocaria” seria a 3ª e 4ª coluna.
Veja abaixo como ficaria o mapa para a divisão dos grupos em A e BC.
5º passo – Agrupando estados da saída
O 5º passo consiste em agrupar os 1’s adjacentes no mapa se for possível. Os 1’s devem ser agrupados em quadrados ou retângulos, sendo que o agrupamento não pode conter nenhum 0.
Além disto, estes quadrados ou retângulos devem conter uma quantidade de 1’s baseada na potência de 2: 2, 4, 8… Os agrupamentos não precisam ser necessariamente adjacentes, pois os 1’s podem ser agrupados entre uma diagonal e outra ou entre as bordas.
E os agrupamentos podem se sobrepor, desde que eles não sejam redundantes (agrupamento que só contém 1’s que já foram agrupados).
Veja a imagem abaixo para entender as possibilidades de agrupamentos:

Na imagem acima, foram feitos: 1 quarteto, 1 octeto e 1 par. Repare que eles se sobrepõem, mas não são redundantes, pois contém 1’s não agrupados por outros.
Retomando nosso exemplo, existem dois agrupamentos possíveis:
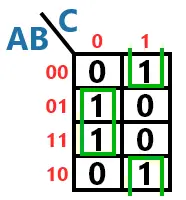
O agrupamento da direita foi feito entre as bordas superior e inferior.
Obs.: Os agrupamentos podem conter don’t care (X) se houver.
6º passo – Extraindo minitermos
O penúltimo passo é extrair o minitermo resultante de cada grupo. Isto é feito observando o estado das entradas dentro do agrupamento. É aqui que aparece o truque do mapa de Karnaugh que foi comentado no início do post.
Se, dentro de um mesmo agrupamento, uma entrada variar seu estado entre duas condições, quer dizer que ela pode ser ignorada. Isto por conta da propriedade da álgebra Booleana mencionada anteriormente.
As demais entradas que não variarem de estado devem ser multiplicadas entre si para criar o minitermo. Entretanto, se a entrada for 0 dentro do agrupamento, ela deve ser multiplicada barrada.
Vamos voltar ao nosso exemplo:
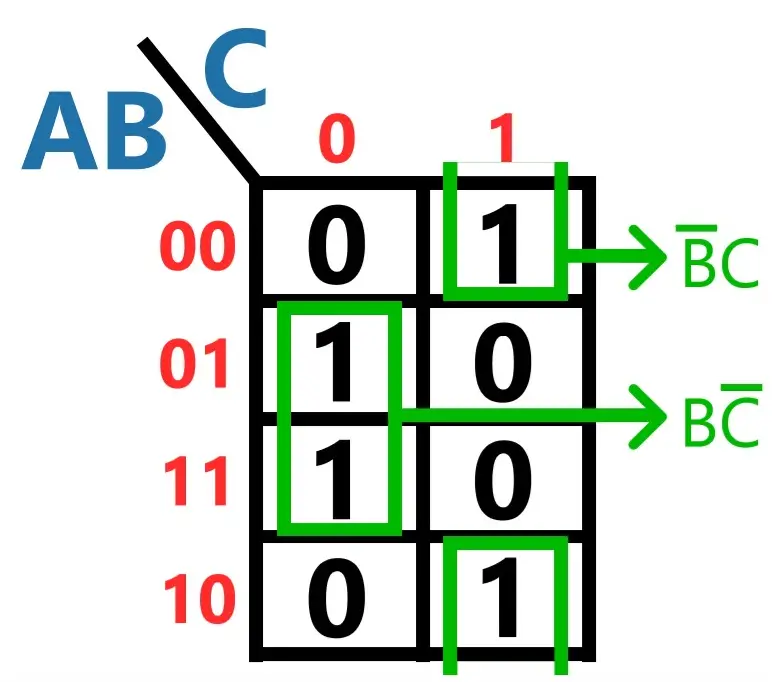
Repare, na imagem acima, que, em ambos os agrupamentos, a entrada A variou. Logo, ela pôde ser ignorada na hora de extrair os dois minitermos.
No agrupamento da esquerda, o estado de B é 1 e de C é 0, por isto o minitermo resultante é B(¬C). No outro, o estado de B é 0 e C é 1. Logo, o minitermo resultante é (¬B)C.
Se não for possível agrupar um 1, basta extrair o minitermo que ele representa multiplicando as entradas entre si e barrando a entrada que estiver em 0.
7º passo – Somando minitermos
Por fim, basta somar todos os minitermos gerados no passo anterior e conferir se o resultado está consistente com a tabela verdade.
Sendo assim, a expressão resultante da saída do nosso exemplo seria:
S = (¬B)C + B(¬C)
Isto nada mais é do que uma operação XOR entre B e C, ou seja, a simplificação máxima da saída S.
Sendo assim, criamos o mapa de Karnaugh da nossa tabela verdade e simplificamos com sucesso a expressão da saída.
Solução alternativa
A obtenção da expressão de saída simplificada poderia ter sido feito por meio dos maxitermos com o agrupamento dos 0’s. Com isto, bastaria multiplicá-los para obter a expressão final da saída.
Mapa com 5 variáveis
Caso você esteja criando um mapa a partir de uma tabela-verdade com 5 variáveis, existe um “truque” para facilitar este processo.
O truque consiste em criar dois mapas diferentes. Sendo que, cada mapa se refere a um estado diferente de uma determinada entrada. Por exemplo: entradas A, B, C, D e E. No mapa 1, consideraremos que é o mapa relativo ao estado da entrada E = 0 e o mapa 2 relativo ao estado de E = 1.
Com isto, o procedimento acima é aplicado normalmente e, no fim da criação dos 2 mapas, os minitermos de ambos são somados.
Observações finais
O procedimento como um todo pode parecer complicado ou demorado. Entretanto, com a prática, você pega o jeito para fazer o mapa e consegue fazê-lo mais rapidamente.
E é perceptível que ele é bem mais vantajoso que a simplificação manual da expressão de saída. Isto porque, com simples passos, obtivemos a expressão de saída simplificada ao máximo sem nenhuma análise mais complicada.
Sendo assim, é sempre recomendável adotar o uso do mapa de Karnaugh na criação de circuitos combinacionais. E, tendo conhecimento desta técnica, já podemos começar a criar sistemas digitais mais elaborados.
Por conta disto, na próxima aula, iremos projetar um circuito digital e montá-lo na prática com a ajuda dos Circuitos Integrados das portas lógicas.
Montando circuito combinacional – Aula 6.2 – ED

Gostei muito da explicação
Que ótimo, Huque. Valeu pelo comentário!
explicação ótima e bem detalhada, obrigada
Que ótimo, fico feliz com o feedback. Obrigado!
É meio complexa mas pude entender alguma coisinha
É um pouco chatinho de entender a princípio mesmo. Recomendo você fazer uns exercícios aplicando a técnica, que aos poucos vai ficando mais fácil entender o processo todo.