Gerar sinal com o Arduino pode ser bem interessante, mas gerar sinal alternado pode ser um problema, principalmente o senoidal. Portanto, vamos ver como criar os seguintes sinais alternados com o Arduino: onda quadrada, onda triangular, onda dente de serra e onda senoidal.
Informações importantes
Antes de entrar nos códigos que geram os sinais, falarei sobre a base teórica necessária para compreender e gerar os sinais.
Geração dos sinais alternados
Os sinais serão gerados por meio um PWM. Isso porque é a forma que temos de gerar sinais “analógicos” em microcontroladores. Sendo assim, se você não sabe o que é o PWM, recomendo a leitura do post sobre o assunto.
Ainda assim, é necessário utilizar outra ferramenta. Antes de falar desta ferramenta, veja a imagem abaixo de um sinal qualquer de PWM.
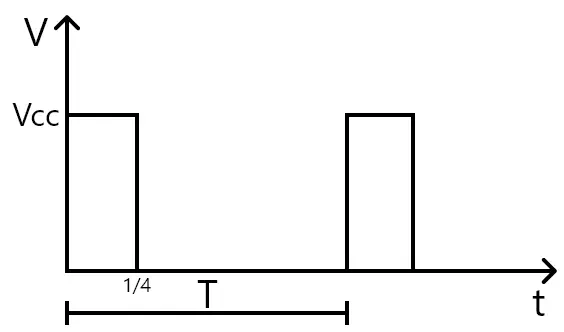
A partir da imagem pode surgir um questionamento: como é possível gerar uma senoide utilizando o PWM, sendo este um sinal pulsado? É isto que será discutido no tópico abaixo.
Transformando PWM em sinal analógico
Sabemos que a tensão média provocada pelo PWM é proporcional ao duty cycle. E esta tensão média é justamente a componente contínua presente no sinal.
Portanto, a outra ferramenta que precisamos é algo que retire a componente alternada do sinal e deixe apenas a contínua. Sendo mais específico, um simples filtro capacitivo passa-baixa é capaz de resolver nosso problema.
O papel do filtro será de atenuar a alta frequência do sinal do PWM e de deixar passar o sinal de baixa frequência (tensão média). Para entender como fazer os cálculos de maneira mais aprofundada, recomendo a leitura do post sobre filtro capacitivo.
Neste ponto, deve-se tomar o cuidado para escolher a frequência de corte adequada. Se ela for muito próxima da frequência do PWM, o sinal de saída possuirá bastante ruido.
Porém, se ela for muito próxima de 0Hz (frequência da componente contínua), a amplitude do sinal de saída será bem pequena. Com isso, o ideal é escolher um valor intermediário. Ao longo do post observaremos isto na prática.
Filtro passa-baixa utilizado
A primeira coisa necessária para o cálculo é a frequência utilizada pelo Arduino para fazer o PWM. Para os pinos 5 e 6 ela é 980Hz e é 490Hz para os demais pinos. Como pretendo utilizar os pinos 5 e 6, considerarei a frequência de 980Hz.
Como o objetivo é eliminar a frequência de 980Hz e manter a componente contínua (0Hz), vou considerar a frequência de corte com um valor entre 100 e 200Hz. Estipulando um capacitor de 100nF e uma frequência de corte de 160Hz:
Arredondando para o valor comercial mais próximo, o resistor utilizado será um de 10kΩ. Portanto, o circuito final será:

Sinal analógico ou digital?
Os sinais gerados não serão exatamente analógicos, pois um sinal analógico possui infinitos valores entre dois pontos quaisquer. Mais detalhes sobre a diferença entre o sinal analógico e o digital podem ser lidos neste post.
Neste caso, o sinal gerado será por meio do pino com PWM do Arduino. E o PWM do Arduino tem um resolução finita de ~20mV. Isto quer dizer que, entre um ponto e outro do sinal resultante, haverá um número finito de valores. Sendo mais específico, existem 256 valores possíveis entre 0 e 5V (incluindo ambos).
Portanto, o sinal gerado será digital, mesmo que não seja um sinal formado por 0’s e 1’s como aparece na eletrônica digital. Entretanto, observando o sinal externamente, será difícil dizer se ele é analógico ou digital.
Gerando sinal com tensão negativa
Se você acompanhou até aqui, foi possível entender como gerar um sinal que varia com o tempo. O que ficou vago foi como gerar um sinal de tensão negativa se, tanto o PWM, quanto o sinal HIGH dos pinos do Arduino são de tensão positiva.
Este problema pode ser resolvido de duas formas:
- A mais simples e intuitiva:
Trocar a referência da medição. O normal é considerar o GND como a referência, mas se ele for invertido com o pino que está sendo medido, será possível medir uma tensão negativa.
Conforme a imagem do tópico anterior, é isto que faremos, porém com a referência no pino 6. Portanto, os sinais de tensão do pino 6 serão negativos.
- A forma mais complicada:
Criar um inversor de tensão, como mostra a imagem abaixo:
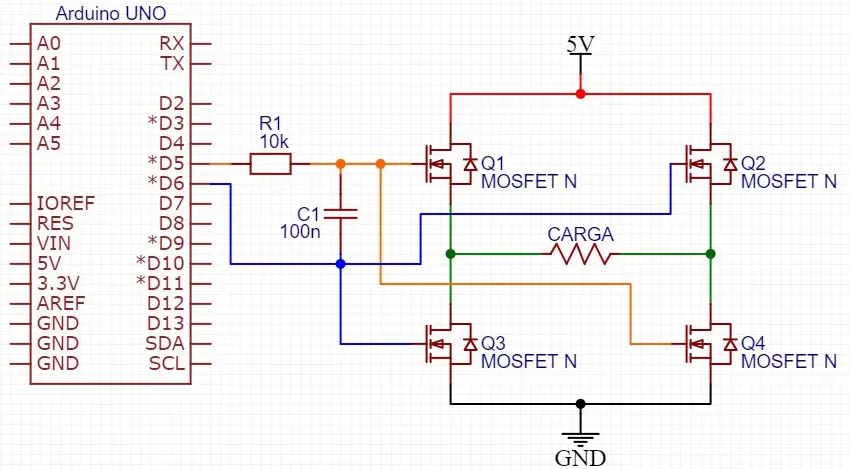
A partir do controle dos MOSFETs, é possível controlar em qual sentido a corrente passa na carga. Sendo assim, podemos controlar o sinal da tensão. Leia o post sobre o inversor de tensão para mais detalhes.
Os sinais que iremos gerar nos tópicos adiantes podem ser utilizados diretamente para controlar os MOSFETs. Com isso, é possível criar sinais alternados de grandes amplitudes e que forneçam altas correntes se uma fonte externa for utilizada para alimentar os MOSFETs.
MAS, para alcançar grande amplitudes de tensão, é necessário utilizar um driver de MOSFET, pois o 5V gerado pelo Arduino não é suficiente para “habilitar” totalmente os MOSFETs. De acordo com uma simulação que fiz, a máxima tensão gerada foi de 1,63V.
Tempo máximo do delay
Para fazer o controle da frequência do sinal, irei utilizar as funções de delay presentes no Arduino. E, neste ponto, é importante ressaltar um detalhe: a função de delay em microssegundos (delayMicroseconds) possui uma precisão limite.
No caso, este limite é de 16383μs. Portanto, sempre que for necessário criar um delay acima deste valor, irei utilizar a função delay mesmo. Enfim, o código do delay possuirá o seguinte aspecto:
1 2 3 4 5 6 7 | // DELAY é uma constante que o programa irá calcular automaticamente para saber // qual o atraso ele deve gerar para criar a frequência certa if(DELAY < 16383){ delayMicroseconds(DELAY); }else{ delay(DELAY/1000); } |
Sinal de onda quadrada
Geração simples
A geração da onda quadrada é bem simples, pois basta colocar o pino em nível lógico alto e depois em nível lógico baixo. Neste ponto não será utilizado o filtro, apenas os pinos 5 e 6 diretamente.
No cabeçalho do programa é possível alterar a frequência do sinal. Ela tem um limite e ele será discutido no tópico abaixo do código.
O código também possui uma definição chamada DELAY, que, neste contexto, diz respeito ao tempo gasto em cada semiciclo. Para saber o tempo do DELAY é só dividir o período (T) por 2.
Código completo
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 | //// Valores que podem ser modificados: // Pinos para de saída #define Vpos 5 #define Vneg 6 // Frequência de saída #define F 30 // Valores que são calculados sozinhos (NÃO MODIFICAR) #define T 1.0/(F) // O atraso é calculado em microssegundos, por isto o período é multiplicado por 1000000 #define DELAY (1000000*T/2.0) void setup(){ pinMode(Vpos, OUTPUT); pinMode(Vneg, OUTPUT); } void loop(){ // Variação de 0 à pi // Manda o pino positivo para HIGH e o negativo para LOW digitalWrite(Vpos, HIGH); digitalWrite(Vneg, LOW); if(DELAY < 16383){ delayMicroseconds(DELAY); }else{ delay(DELAY/1000); } // Variação de pi à 2pi // Manda o pino positivo para LOW e o negativo para HIGH digitalWrite(Vpos, LOW); digitalWrite(Vneg, HIGH); if(DELAY < 16383){ delayMicroseconds(DELAY); }else{ delay(DELAY/1000); } } |
Análise do sinal de saída
Utilizando o código acima, coloquei uma frequência de 100Hz (#define F 100) e fiz upload do código. Com isso, medi o sinal utilizando um osciloscópio ligado diretamente nos pinos 5 e 6.
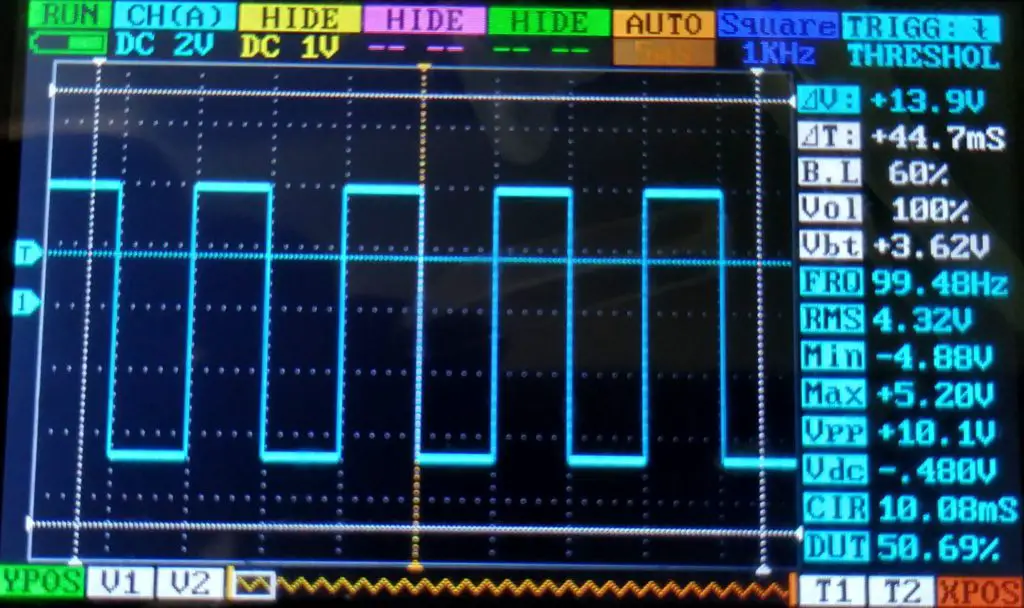
O sinal de saída foi bem limpo (sem ruido), com uma frequência próxima àquela estipulada no código e com uma amplitude próxima do esperado. Entretanto, isto não permanece quando incrementamos bastante a frequência.
Resolvi colocar a frequência em um valor muito alto para observar qual seria a frequência limite. O resultado está mostrado abaixo.
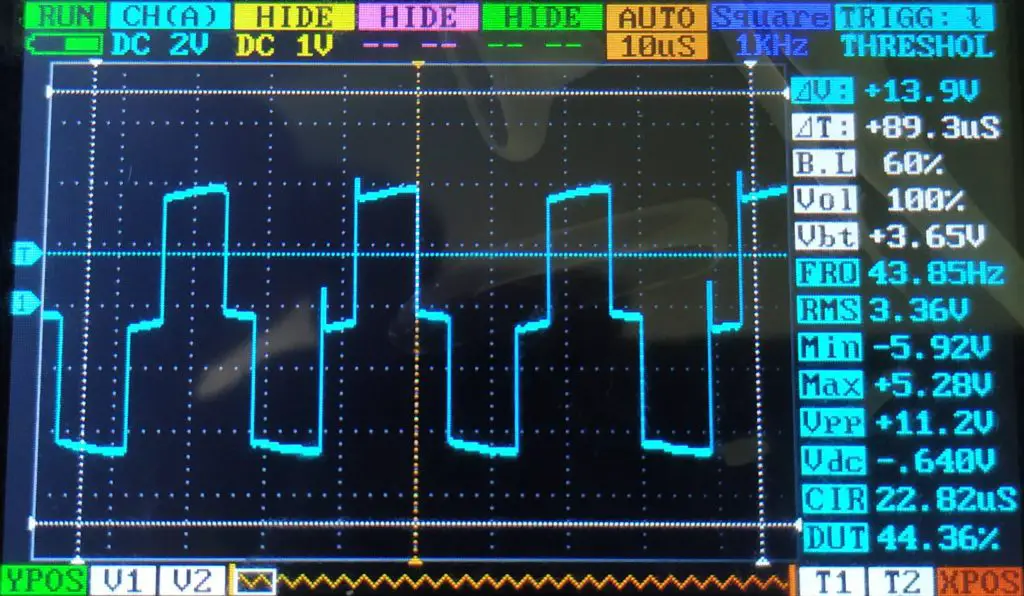
A frequência indicada não está correta, pois o certo seria 43.85kHz. É possível confirmar isso olhando a divisão de tempo e o sinal (1 período ~= 2 quadrados ~= 20μs ~= 43.85kHz).
É possível perceber que o sinal não se parece exatamente com uma onda quadrada, pois ele fica em 0v por uma parcela considerável do período. Além disso, há pequenos ruídos no sinal.
Enfim, de acordo com testes que fiz, a máxima frequência que produz um bom sinal, é cerca de 10kHz. Mas, se alterássemos diretamente o funcionamento dos timers do atmega328p, poderíamos aumentar este sinal máximo de saída.
Geração com amplitude variável
Apesar do código acima funcionar corretamente, pode ser o caso de você desejar alterar a amplitude da onda quadrada. Para este caso, será necessário utilizar o PWM.
Conforme abordado anteriormente, é necessário utilizar um filtro passa-baixa para converter o sinal do PWM em tensão média. E o circuito utilizado será o do tópico “Filtro passa-baixa utilizado”.
Enfim, o código agora é bem parecido com o anterior. A diferença é que, ao invés de colocar as saídas em HIGH ou LOW, iremos controlar o nível de tensão delas pelo PWM. Sendo assim, bastará utilizar o comando analogWrite para controlar qual será a amplitude da onda quadrada.
Os parâmetros do código são os mesmos de antes, com a adição do parâmetro Vmax, que diz respeito à amplitude em termos de tensão. Com base neste parâmetro o programa calcula a amplitude em termos do PWM fazendo uma regra de 3.
O parâmetro DELAY é subtraído em 12 unidades para compensar o atraso gerado pela função analogWrite. Este valor foi descoberto experimentalmente.
Código completo
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 | //// Valores que podem ser modificados: // Pinos para o PWM #define Vpos 5 #define Vneg 6 // Tensão máxima (0-5v) e Frequência de saída #define VMAX 3.17 #define F 30 // Valores que são calculados sozinhos (NÃO MODIFICAR) #define AMPLITUDE VMAX*(255.0/5.0) #define T 1.0/(F) #define DELAY (1000000*T/2.0 - 12) void setup(){ // Não é necessário definir os pinos como saída } void loop(){ // Variação de 0 à pi analogWrite(Vpos, AMPLITUDE); analogWrite(Vneg, 0); if(DELAY < 16383){ delayMicroseconds(DELAY); }else{ delay(DELAY/1000); } // Variação de pi à 2pi analogWrite(Vpos, 0); analogWrite(Vneg, AMPLITUDE); if(DELAY < 16383){ delayMicroseconds(DELAY); }else{ delay(DELAY/1000); } } |
Análise do sinal de saída
Utilizando o código acima, coloquei uma frequência de 30Hz (#define F 30) e uma amplitude de 3,17V (#define VMAX 3.17). Antes de medir o sinal na saída do filtro, resolvi medir o sinal direto nos pinos 5 e 6. Fiz isto para vermos como é o formato do PWM para este caso.
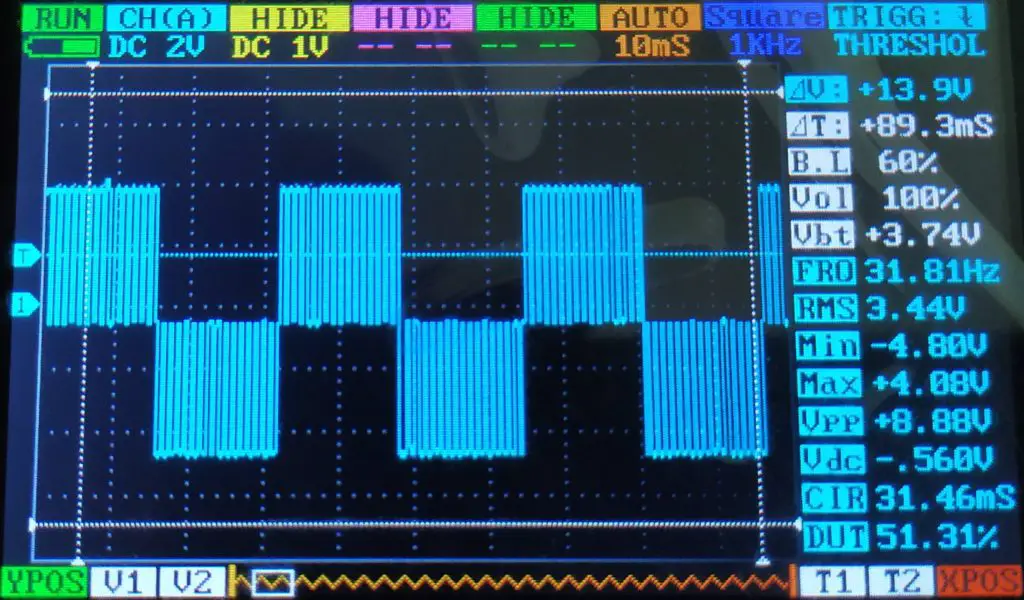
O resultado parece estar dentro do esperado, pois a frequência é cerca de 30Hz e o sinal varia entre positivo e negativo. O único problema está no valor máximo (4.08V), que deveria ser 5V, já que o valor máximo é o sinal de nível alto do PWM (5v).
Agora, vamos ver como é o sinal de saída do filtro capacitivo:
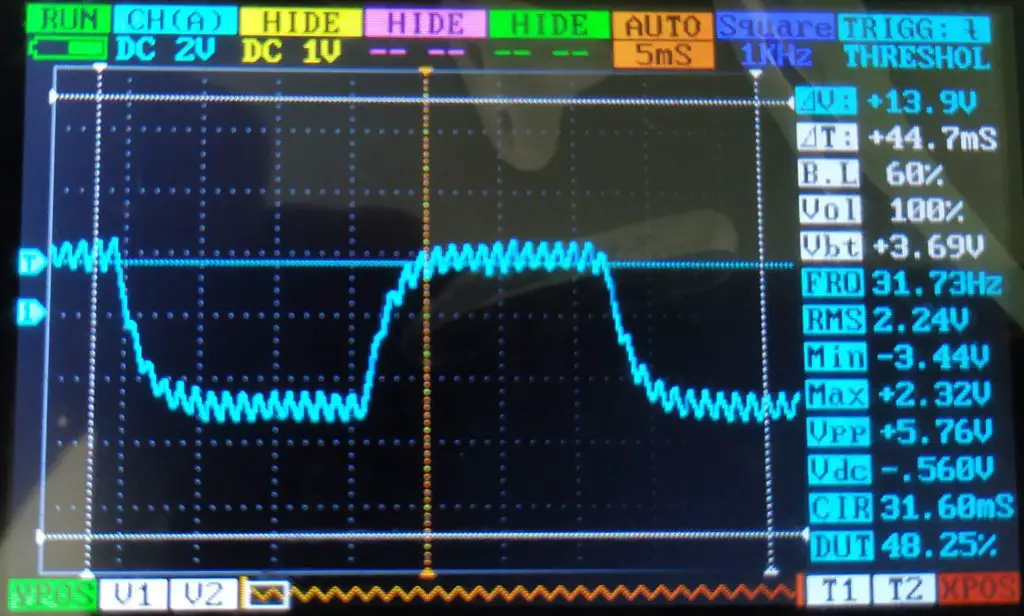
Tirando os ruídos de lado, é interessante ver o que o filtro fez com os sinais pulsados da penúltima imagem. A frequência do sinal continua próxima dos 30Hz, porém a amplitude está um pouco longe do esperado.
Se considerarmos a metade da tensão de pico-a-pico (5,76V), a amplitude foi de 2,88V, isto é, ~0,3V distante do esperado. Apesar disto, o código é capaz de criar uma onda quadrada de amplitude variável com uma exatidão razoável.
O último ponto interessante de ser mencionado é a frequência limite do sinal. De acordo com testes que realizei, até 80Hz o sinal de saída é razoavelmente bom. Acima disto, a distorção começa a aumentar significativamente.
Novamente, é possível aumentar esta frequência limite configurando diretamente os timers do atmega328p.
Sinal de onda triangular
Geração do sinal
Para gerar a onda triangular, podemos decompor o sinal em 4 partes: a subida de 0V até +Vpico; a descida de +Vpico até 0V; a descida de 0V até -Vpico; e a subida de -Vpico até 0V.
E, parar gerar cada parte, basta ir incrementando/decrementando o duty cycle do PWM de forma linear. Isto pode ser feito com um simples for. Como são 4 partes, utilizarei 4 estruturas for. Sendo que as amplitudes negativas são geradas aplicando o PWM no pino 6 e as positivas no pino 5.
Os parâmetros utilizados pelo programa são os mesmos de antes. Entretanto, o cálculo do DELAY é diferente. Como o sinal será dividido em 4 partes, o DELAY será a divisão do período (1/F) por 4. Além disso, cada subida/descida será feita variando 1 unidade até alcançar a amplitude.
Por exemplo, uma amplitude de 255 (valor máximo do PWM). Para alcançar esta amplitude, o programa irá subir de 0 até 255 incrementando uma unidade por passo. Portanto, o DELAY deve dividir o período pela amplitude + 1 unidade. O +1 é porque a contagem é feita de 0 a 255 (inclui os extremos).
Ademais, DELAY é subtraído em 6 unidades para compensar o atraso gerado pela função analogWrite. Este valor foi descoberto experimentalmente.
Código completo
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 | //// Valores que podem ser modificados: // Pinos para o PWM #define Vpos 5 #define Vneg 6 // Tensão máxima (0-5v) e Frequência de saída #define VMAX 5 #define F 30 // Valores que são calculados sozinhos (não modificar) #define AMPLITUDE VMAX*(255.0/5.0) #define T 1.0/(F) #define DELAY (T*1000000.0)/((AMPLITUDE+1)*4) - 6 void setup(){ } void loop(){ // Variação de 0 à pi/2 da onda for(int i = 0; i <= AMPLITUDE; i++){ analogWrite(Vpos, i); if(DELAY < 16383){ delayMicroseconds(DELAY); }else{ delay(DELAY/1000); } } // Variação de pi/2 à pi da onda for(int i = AMPLITUDE; i >= 0; i--){ analogWrite(Vpos, i); if(DELAY < 16383){ delayMicroseconds(DELAY); }else{ delay(DELAY/1000); } } // Variação de pi à 3pi/2 da onda for(int i = 0; i <= AMPLITUDE; i++){ analogWrite(Vneg, i); if(DELAY < 16383){ delayMicroseconds(DELAY); }else{ delay(DELAY/1000); } } // Variação de 3pi/2 à 2pi da onda for(int i = AMPLITUDE; i >= 0; i--){ analogWrite(Vneg, i); if(DELAY < 16383){ delayMicroseconds(DELAY); }else{ delay(DELAY/1000); } } } |
Análise do sinal de saída
Utilizando o código acima, coloquei uma frequência de 30Hz (#define F 30). Antes de medir o sinal na saída do filtro, resolvi medir o sinal puro do PWM (direto nos pinos 5 e 6).
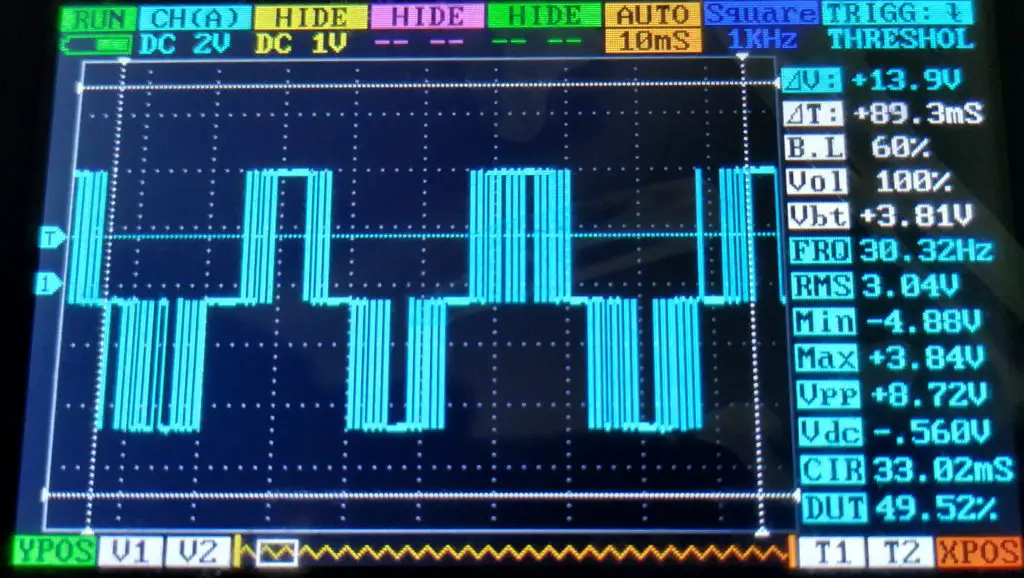
O sinal está de acordo com a expectativa, por conta da frequência de 30Hz e alternância entre positivo e negativo. Assim como o sinal de onda quadrada, a amplitude está longe do esperado.
Enfim, o mais interessante de analisar é o aumento da largura dos pulsos. Onde seria o pico da onda triangular é possível reparar uma maior constância do pulso, devido a alta amplitude neste ponto.
Agora vamos ver como é o sinal filtrado:
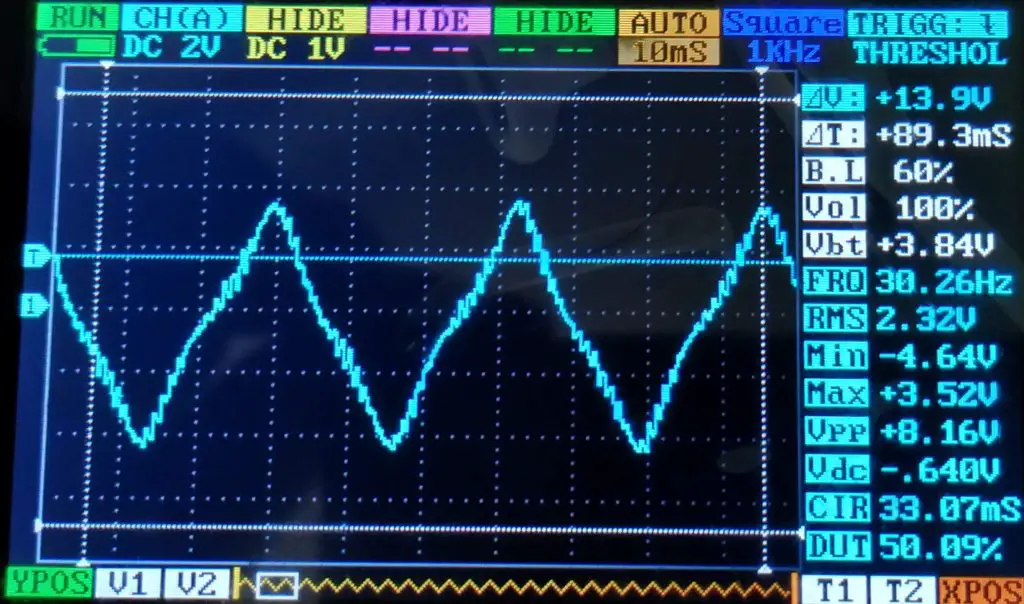
A partir da imagem acima, podemos tirar as mesmas conclusões: frequência próxima do valor inserido e amplitude abaixo do esperado. Além disso, assim como a onda quadrada, há presença de ruídos no sinal.
Entretanto, ainda é bastante intrigante observar o efeito que o filtro provocou no sinal com PWM.
Seguindo o mesmo padrão do sinal de onda quadrada, à medida que a frequência aumenta, a amplitude do sinal cai e os ruídos aumentam. E a frequência limite que encontrei foi cerca de 120Hz. Acima disto, a qualidade da onda fica muito ruim.
Pra finalizar, também fiz um teste variando a amplitude do sinal para 2,63V (#define Vmax 2.63). O resultado pode ser visto abaixo.
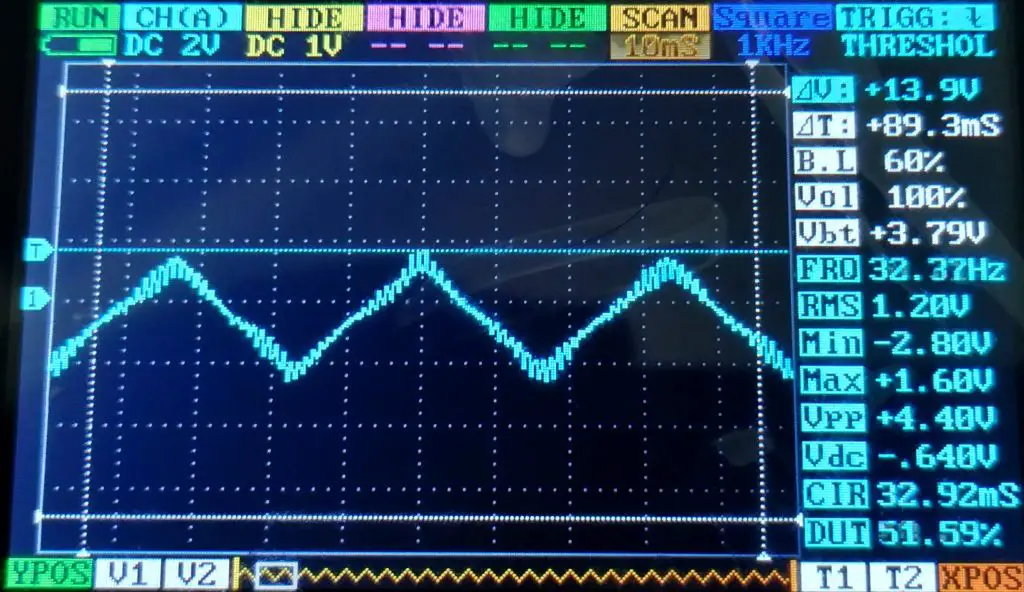
Considerando a tensão de pico como sendo Vpp/2: Vp=2,20V. Seguindo novamente o mesmo padrão da onda quadrada, a exatidão da amplitude é bem razoável.
Sinal de onda dente de serra
Geração do sinal
A geração da onda dente de serra pode ser decomposta em 2 partes: a subida positiva de 0V até +Vpico; e a subida negativa de -Vpico até 0V.
E, a onda dente de serra possui um formato muito parecido com a onda triangular. Por conta disso, o código não é muito diferente, sendo necessário o mesmo procedimento de incremento linear do duty cycle.
Os parâmetros utilizados são os mesmos de antes. Desta vez, o DELAY é o período dividido por 2 devido às duas partes do sinal. Alem disso, será necessário dividir o DELAY pela amplitude + 1 unidade por causa dos mesmos fatores de antes.
Ademais, DELAY é subtraído em 6 unidades para compensar o atraso gerado pela função analogWrite. Este valor foi descoberto experimentalmente.
Código completo
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 | //// Valores que podem ser modificados: // Pinos para o PWM #define Vpos 5 #define Vneg 6 // Tensão máxima (0-5v) e Frequência de saída #define VMAX 5 #define F 30 // Valores que são calculados sozinhos (não modificar) #define AMPLITUDE VMAX*(255.0/5.0) #define T 1.0/(F) #define DELAY (T*1000000.0)/((AMPLITUDE+1)*2) - 6 void setup(){ } void loop(){ // Variação de 0 à pi da onda for(int i = 0; i <= AMPLITUDE; i++){ analogWrite(Vpos, i); if(DELAY < 16383){ delayMicroseconds(DELAY); }else{ delay(DELAY/1000); } } // Volta o PWM para 0 analogWrite(Vpos, 0); // Variação de pi à 2pi da onda for(int i = AMPLITUDE; i >= 0; i--){ analogWrite(Vneg, i); if(DELAY < 16383){ delayMicroseconds(DELAY); }else{ delay(DELAY/1000); } } } |
Análise do sinal de saída
Coloquei uma frequência de 30Hz (#define F 30). Novamente, medi primeiro o sinal puro do PWM (direto nos pinos 5 e 6). Ignore a medição da frequência do display na imagem abaixo e considere a frequência pelos quadrados. T ~= 3 quadrados ~= 30mS ~= 30Hz.
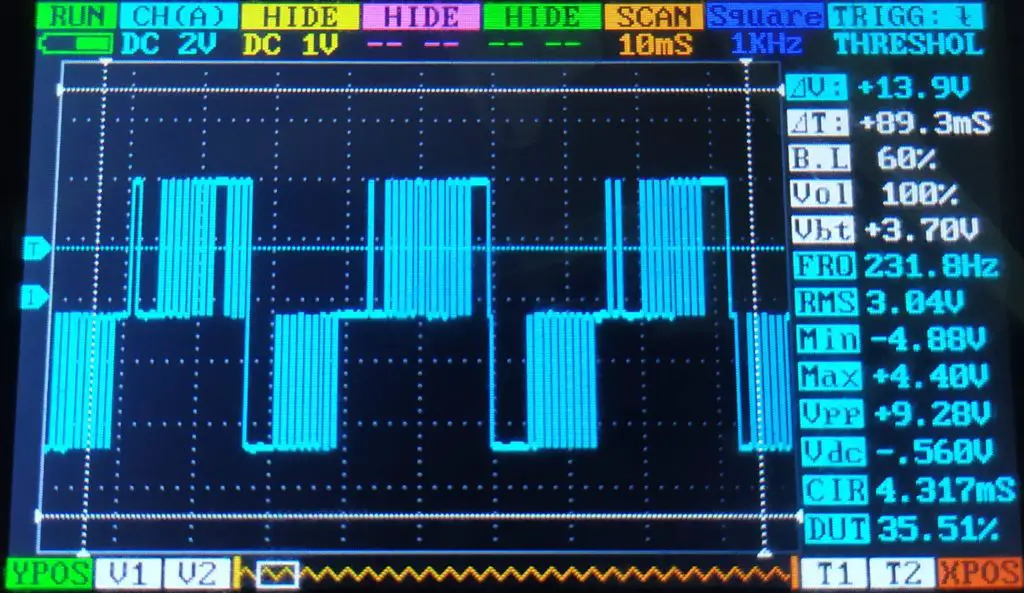
Conclusão: frequência próxima do esperado, amplitude distante da desejada e sinal alternando entre positivo e negativo A conclusão não distoa com o observado nos demais casos.
Enfim, a parte instigante é a variação da largura dos pulsos, que começa nula e vai aumentando até o topo do dente de serra. E depois, ela já vai para a parte negativa com a largura com um tamanho considerável e vai reduzindo até os 0V.
Agora vamos analisar a onda filtrada:
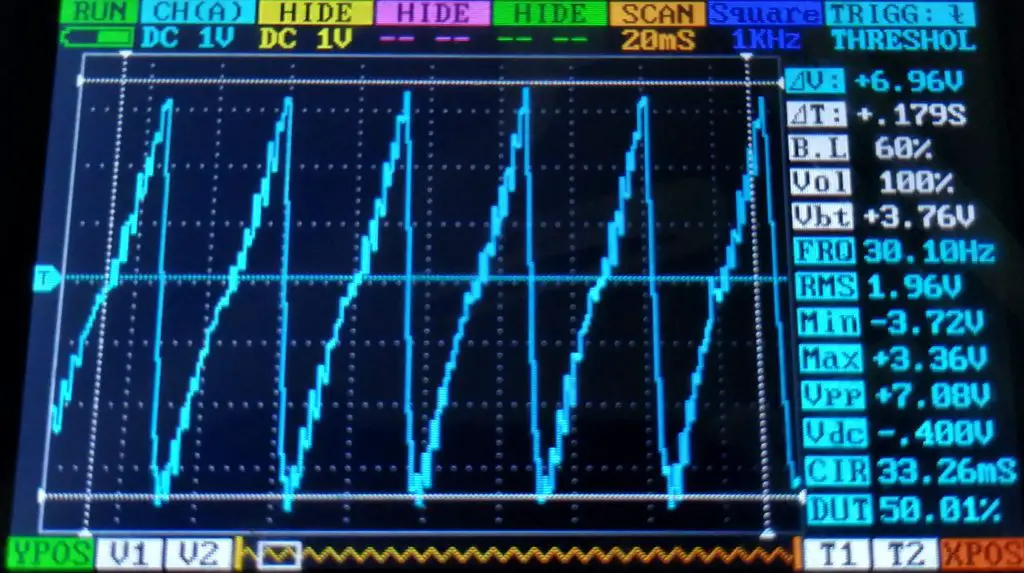
A partir da imagem acima, podemos comprovar que a frequência é de fato bem próxima da prevista. Outra vez, a onda possui as mesma características: amplitude longe do almejado e presença de ruídos no sinal.
Onda senoidal
Variação senoidal do PWM
Talvez a senoide seja a mais complexa dentre as ondas apresentadas até então. O principal motivo é como gerar a variação do PWM. Isso porque antes ela era linear, agora a variação deve ser senoidal.
A resolução simplificada do problema é fazer incrementos lineares em um ANGULO que varia de 0 até 2π para, então, calcular o seno do ângulo. E a variação seria calculada considerando a frequência do sinal.
Para isso, temos a função sin, que advêm da biblioteca math.h que é capaz de calcular o seno de um ângulo. Contudo, existe um grande problema que é o atraso gerado por esta função.
De acordo com testes que realizei, este atraso é bastante significativo. Tanto que os atrasos combinados de todas as chamadas da função foram capazes de aumentar o período em 1s. Ou seja, a frequência não podia ser acima de 1Hz.
Enfim, para contornar este obstáculo, podemos criar um vetor com todos os valores de seno já calculados. O programa abaixo que fiz em python foi capaz de gerar esta lista, que varia o ângulo linearmente em 256 partes iguais indo de 0 a π/2. Não pretendo explicar o programa, pois não é assunto direto do post, até porque os comandos são simples.
1 2 3 4 5 6 7 8 9 10 | import math import numpy as np step = math.pi/(2*255) pwm = [] for i in np.arange(0, math.pi/2+step, step): pwm.append(round(math.sin(i)*255)) print(pwm) |
Geração do sinal
Após resolver o problema mostrado no tópico anterior, podemos partir para o método de geração do sinal. Uma forma simples seria dividir a senoide em 4 partes: a subida de 0 a π/2; a descida de π/2 a π; a descida de π/2 a 3π/2; e a subida de 3π/2 até 2π.
Para cada parte, basta criar uma variável que é incrementada/decrementada linearmente, sendo que, em cada instante, esta variável é utilizada para acessar uma posição do vetor criado no tópico anterior.
De novo, os parâmetros utilizados aqui serão os mesmos que os dos demais programas, com exceção de DELAY. Neste caso, DELAY é calculado da mesma forma que na onda triangular (divide o período por 4 e por amplitude + 1).
Ademais, DELAY é subtraído em 6 unidades para compensar o atraso gerado pela função analogWrite. Este valor foi descoberto experimentalmente.
Código completo
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 | //// Valores que podem ser modificados: // Pinos para o PWM #define Vpos 5 #define Vneg 6 // Tensão máxima (0-5v) e Frequência de saída #define VMAX 5 #define F 60 // Valores que são calculados sozinhos (não modificar) #define AMPLITUDE VMAX*(255.0/5.0) #define T 1.0/(F) #define DELAY (T*1000000.0)/((AMPLITUDE+1)*2*2) - 6 // Vetor de 256 posições contendo às amplitudes do PWM variando de forma senoidal const char seno[] = { 0, 2, 3, 5, 6, 8, 9, 11, 13, 14, 16, 17, 19, 20, 22, 24, 25, 27, 28, 30, 31, 33, 34, 36, 38, 39, 41, 42, 44, 45, 47, 48, 50, 51, 53, 55, 56, 58, 59, 61, 62, 64, 65, 67, 68, 70, 71, 73, 74, 76, 77, 79, 80, 82, 83, 85, 86, 88, 89, 91, 92, 94, 95, 96, 98, 99, 101, 102, 104, 105, 107, 108, 109, 111, 112, 114, 115, 116, 118, 119, 121, 122, 123, 125, 126, 127, 129, 130, 132, 133, 134, 136, 137, 138, 140, 141, 142, 143, 145, 146, 147, 149, 150, 151, 152, 154, 155, 156, 157, 159, 160, 161, 162, 164, 165, 166, 167, 168, 169, 171, 172, 173, 174, 175, 176, 178, 179, 180, 181, 182, 183, 184, 185, 186, 187, 188, 190, 191, 192, 193, 194, 195, 196, 197, 198, 199, 200, 201, 202, 203, 203, 204, 205, 206, 207, 208, 209, 210, 211, 212, 213, 213, 214, 215, 216, 217, 218, 218, 219, 220, 221, 222, 222, 223, 224, 225, 225, 226, 227, 228, 228, 229, 230, 230, 231, 232, 232, 233, 234, 234, 235, 235, 236, 237, 237, 238, 238, 239, 239, 240, 241, 241, 242, 242, 243, 243, 243, 244, 244, 245, 245, 246, 246, 247, 247, 247, 248, 248, 248, 249, 249, 249, 250, 250, 250, 251, 251, 251, 251, 252, 252, 252, 252, 253, 253, 253, 253, 253, 254, 254, 254, 254, 254, 254, 254, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255 }; void setup(){ } void loop(){ // Variação de 0 à pi/2 da onda for(int i = 0; i <= AMPLITUDE; i++){ analogWrite(Vpos, seno[i]); if(DELAY < 16383){ delayMicroseconds(DELAY); }else{ delay(DELAY/1000); } } // Variação de pi/2 à pi da onda for(int i = AMPLITUDE; i >= 0; i--){ analogWrite(Vpos, seno[i]); if(DELAY < 16383){ delayMicroseconds(DELAY); }else{ delay(DELAY/1000); } } // Variação de pi à 3pi/2 da onda for(int i = 0; i <= AMPLITUDE; i++){ analogWrite(Vneg, seno[i]); if(DELAY < 16383){ delayMicroseconds(DELAY); }else{ delay(DELAY/1000); } } // Variação de 3pi/2 à 2pi da onda for(int i = AMPLITUDE; i >= 0; i--){ analogWrite(Vneg, seno[i]); if(DELAY < 16383){ delayMicroseconds(DELAY); }else{ delay(DELAY/1000); } } } |
Análise do sinal de saída
Seguindo o padrão, utilizei uma frequência de 30Hz. Novamente, medi primeiro o sinal puro do PWM (direto nos pinos 5 e 6).
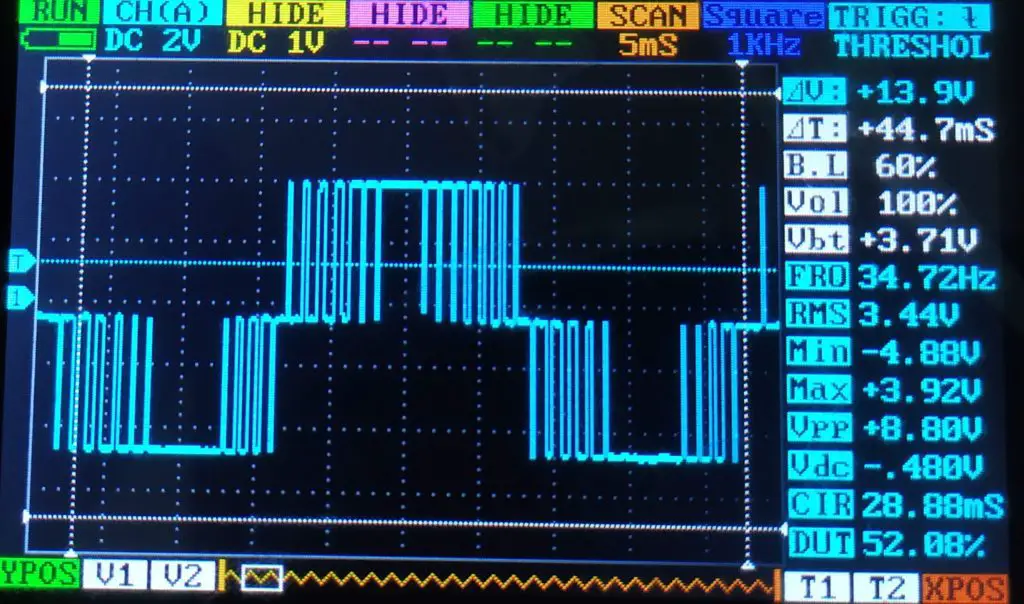
Pela 4ª vez: frequência próxima da expectativa, amplitude distante e sinal alternado. E, reforço novamente a análise sob a variação da largura dos pulsos.
Apesar do PWM ser um pulso, é possível distinguir os 4 tipos de ondas apenas pelo sinal de PWM. Repare que, agora, o pulso começa pequeno, vai aumentando e tem largura considerável em π/2 e 3π/2, que são os pontos da tensão de pico positiva e negativa respectivamente.
Vejamos agora o sinal filtrado:
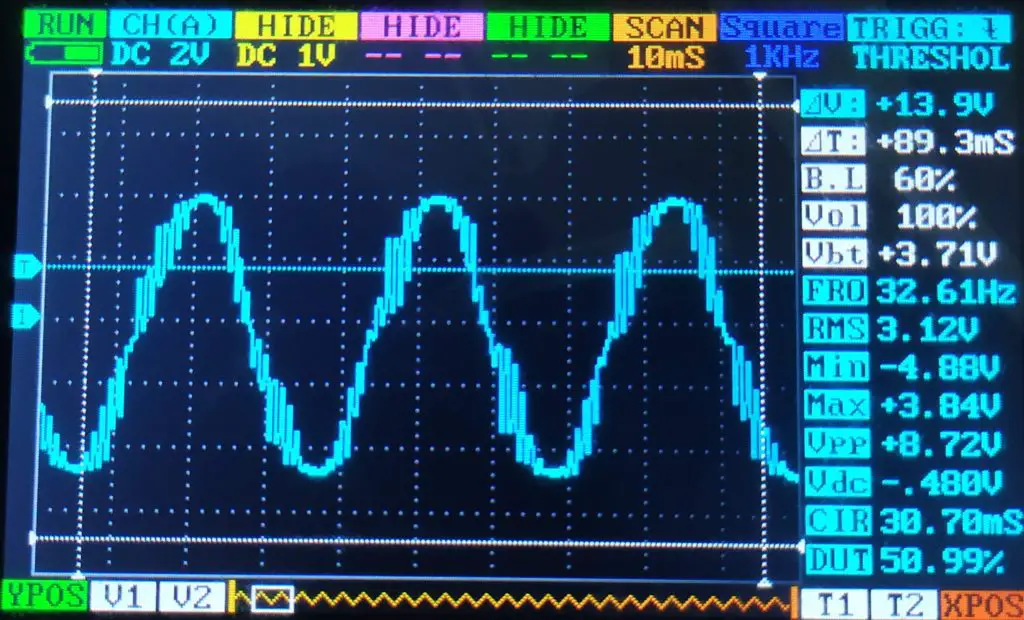
Conforme vimos nas demais ondas, a amplitude está distante do aguardado e o sinal possui ruídos. De toda forma, é possível perceber que o filtro foi capaz de transformar o PWM em uma senoide.
Para melhorar a onda, resolvi mudar o filtro e colocar uma frequência de corte baixa (~7Hz). O resultado foi bem satisfatório, porém a amplitude reduziu um pouco. Obs.: resolvi colocar uma frequência de 20Hz para testar.
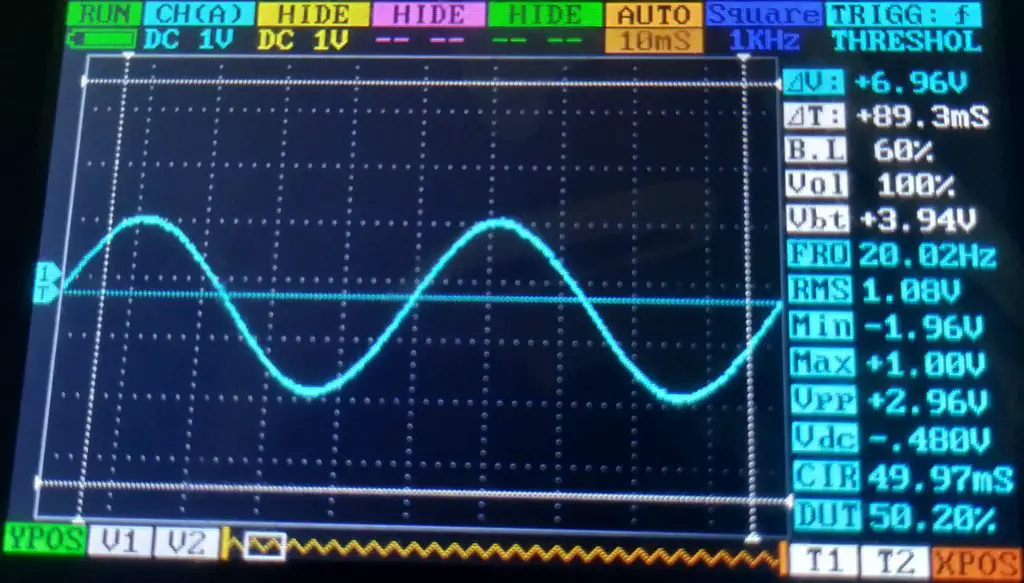
De acordo com a imagem acima, não é possível perceber nenhum ruído. Portanto, o sinal ficou muito bom (ignorando a amplitude). A senoide ficou praticamente perfeita.
Obs: a frequência máxima da onda senoidal é cerca de 80Hz.
Melhorando o sinal de saída
Os sinais de saída de todas as ondas apresentaram uma quantidade considerável de ruído. Existem algumas formas diferentes de resolver este problema, mas a mais simples e direta seria reduzir a frequência de corte, assim como foi mostrado no tópico acima.
O problema disto é que a amplitude do sinal de saída é significativamente reduzida. Portanto, preferi deixar o filtro do jeito que mostrei para facilitar a visualização do sinal. Uma solução para este problema da amplitude é amplificar o sinal com um transistor.
O ideal mesmo seria utilizar os sinais gerados para controlar o circuito de um inversor de tensão, assim como foi discutido no início do post.
Ou então, seguir com a ideia do post abaixo:
Gerando sinal alternado com MCP4725

foi boa sua explicação eu estou tentando gerar um sinal de onda quadrada 60-2 mas ainda não consegui gerar vc tem uma explicativa de como gerar essa onda
Obrigado, Marcos! Para te ajudar preciso entender o que seria exatamente uma onda quadrada 60-2. Seria ela uma onda de 60Hz e 2V de pico?
Oi Fábio, parabéns pela publicação, ótimo conteúdo e didática. Quanto ao código da variação senoidal do PWM tentei executar aqui mas não está funcionando. O programa está compilando, mas quando eu fui simular no proteus (usando um módulo de arduino), não apareceu nada no osciloscópio. Me ajuda ai por favor.
Olá, Felipe. Eu é que agradeço pelo retorno positivo!
Então, quando fui simular no proteus, o sinal de saída estava um pouco estranho mesmo. Mas aparecia alguma coisa que lembrava uma senoide. O problema que você está tendo pode ter várias causas, mas vou desconsiderar que o problema seja do código, pois eu o testei diversas vezes na prática. Para verificar se o problema é com o Proteus, tente rodar um código simples do Arduino (código blink por exemplo). Se funcionar, tente ver se, com o código da senoide, os pinos 5 e 6 apresentam qualquer tipo de variação para verificar se o código está sendo interpretado corretamente pelo Proteus. Enfim, são muitas possibilidades. Qualquer coisa, me mande no e-mail (mundoprojetado@gmail.com) o seu arquivo do proteus e o arquivo do código que você está utilizando na simulação para eu replicar aqui e conseguir te ajudar melhor.
Excelente, meus parabéns pelo conteúdo
Muitíssimo obrigado, Hyggor! Fico feliz que tenha gostado do conteúdo.
Muito boa a postagem !!!! Mas não consigo entender como é feita a conexão do circuito do inversor de tensão com o arduino, é colocado os pinos analógicos do arduino em qual parte do circuito inversor de tensão?
Obrigado, Eduardo! Utilizando a imagem do inversor mostrada como referência, você precisaria ligar uma das saídas analógicas nos transistores Q1 e Q4 e a outra saída analógica nos transistores Q2 e Q3. Desta forma, é como se cada saída analógica controlasse o fluxo da corrente no inversor de tensão. Se ainda assim você estiver com dúvida, retorne o contato que eu faço um desenho para exemplificar melhor.
Realmente não entendi como vou colocar uma saída em dois transistores que não contém nenhuma ligação. Teria como fazer o desenho?
Claro! Veja se agora está mais claro: escopo da ligação. Se você achar legal, posso fazer um post focado nesta parte do sinal alternado com mosfet.
Olá, Eduardo. Sei que já faz um tempo, mas havia um equívoco no circuito dos Mosfets que te passei e no que coloquei no post. Se quiser dar uma olhada, eu fiz a correção e testei aqui.
Fabio, parabéns pela excelente explicação, muito didática e proveitosa… conheci a pouco tempo o ” mundo projetando” e estou adorando, muito bom trabalho, Parabéns!!
Muitíssimo obrigado, Leonidas! É excelente saber que o conteúdo do site está sendo prestativo. Espero poder continuar trazendo bons assuntos! Abraço.
Assunto bem interessante. Parabéns e obrigado
Eu é que agradeço pelo comentário, André! Espero que os demais assuntos do site te interessem também.
Olá Fábio! Estou usando o acelerometro mpu 6050 no meu projeto, e preciso fazer uma FFT dos dados de aceleração x tempo e passar pro dominio da frequencia. Porém, estou com problemas, pois o acelerometro é muito sensivel. Me foi recomendado um filtro passa baixa de 2 ordem para melhorar o sinal de saída analógica. Poderia me ajudar a montar o esquema do circuito com esse filtro?
Olá, Emilio! Posso te ajudar sim, mas existe um pequeno problema em se fazer isto. Acontece que os dados de aceleração do MPU6050 são extraídos de forma digital, via interface I2C. Então, não é possível utilizar um filtro analógico diretamente para se livrar dos ruídos do sensor. Para isto, você teria que converter estes dados em valores analógicos, possivelmente com um conversor DA, para então aplicar em um filtro analógico, conforme você disse.
Outra solução mais direta é utilizar um filtro digital para filtrar os ruídos advindos da própria saída digital do MPU6050. Até o momento eu só conheço o filtro de Kalman, que é um algoritmo bastante interessante, mas que pode ser um tanto quanto complexo de implementar.
Cabe a você decidir qual o melhor caminho a ser tomado, pois eu não tenho experiência suficiente para dizer qual seria o mais adequado para este caso. Enfim, pode retornar o contato pelo meu email, que te ajudo melhor por lá: mundoprojetado@gmail.com
Olá Fábio, obrigado pelo posto, queria para uma aplicação, levar a frequência da rede de 60hz para 240hz, conseguiria me ajudar em como fazer isso?
Olá, Paulo. Obrigado pelo comentário. Deixe-me entender alguns pontos antes. A sua ideia seria pegar a tensão da rede de 60Hz, 127Vrms e convertê-la em 240Hz, 127Vrms? E a tensão convertida precisa ser uma senoide também?
Bom dia!estou testando no proteus a simulação da senoide, notei que o semi circulo negativo, não é gerado(Vneg), poderia me ajudar com essa dúvida?
Bom dia, Delton. Difícil te dizer qual é o problema exatamente, mas é bem provável que tenha relação com a referência da leitura da tensão (que por padrão é o GND). O sinal de saída tem que ser medido entre os dois pontos mostrados nesta imagem. Então, para fazer isso, você poderia colocar o pino D5 no canal ‘A’ do osciloscópio e o pino D6 no canal ‘B’ do osciloscópio. Com isto, você aplica uma função matemática ‘A-B’ no osciloscópio (acho que você faz isto marcando o ‘A+B’ no canal ‘A’ e invertendo o canal ‘B’).
eu queria usar esse esquema para fazer um inversor de baixa potencia colocando um transformador na saida dos mosfets, sendo o sinal vindo do arduino, a fonte dos mosfets seria 12v, mas estou com dificuldades, parece que para os mosfets tenho que aumentar a tensao e tbem eles nao estao simulando bem, começa mas da erro
Olá, Marco Antonio. Dependendo do caso, acredito que seja necessário o uso de um driver pra acionar os MOSFETs. Recomendo você ver este vídeo e a parte 2 dele, pois eles podem te ajudar a entender seu problema.