Os filtros capacitivos passa-baixa e passa-alta são bem úteis em processamento simples de sinais. Portanto, vamos ver como os filtros de 1ª ordem funcionam.
Informações importantes
O entendimento das componentes dos sinais elétricos é imprescindível para o bom entendimento dos filtros. Sendo assim, o post que fala sobre as componentes dos sinais elétricos é de leitura obrigatória para este.
Por conta disso, utilizarei alguns dos conceitos abordados neste outro post. E estarei me referindo ao sinal como o sinal elétrico analógico de tensão.
Filtro passa-baixa
Definição básica
O filtro passa-baixa é um circuito que permite a passagem de sinais de baixa frequência ao mesmo tempo que reduz a intensidade de sinais de alta frequência.
Isto é, a partir de uma frequência de referência, ele permite que frequências mais baixas que ela passem livremente. E frequências mais altas são atenuadas (reduzidas em amplitude).
O circuito deste tipo de filtro é composto por uma resistência em série com um capacitor. Sendo que, o sinal de saída filtrado fica em paralelo com o capacitor.
Veja a imagem abaixo para entender:
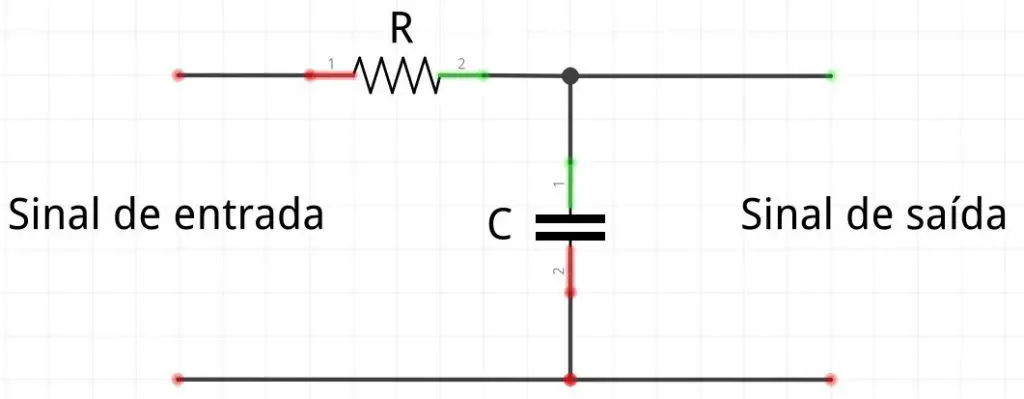
O sinal de entrada pode ser qualquer tipo de sinal alternado ou contínuo. E o sinal de saída será o sinal de entrada sem as frequências mais altas que a frequência de referência.
Filtro passa-alta
Definição básica
O filtro passa-alta é um circuito que facilita a passagem de sinais de alta frequência enquanto diminui a intensidade de sinais de baixa frequência.
Isto é, a partir de uma frequência de referência, ele permite que frequências mais altas que ela passem livremente. E frequências mais baixas são atenuadas.
O circuito deste tipo de filtro é similar ao anterior, com a diferença de que os componentes (resistor e capacitor) estão trocados de posição. Por conta disso, o sinal de saída filtrado fica em paralelo com o resistor.
Veja a imagem abaixo para entender:
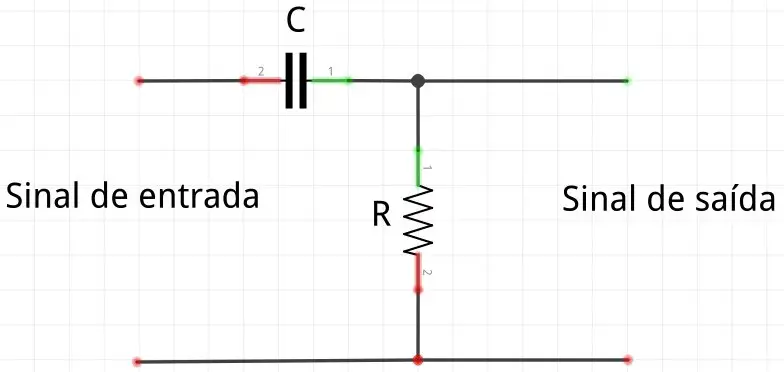
O sinal de saída será o sinal de entrada sem as frequências mais baixas que a frequência de referência.
Funcionamento dos filtros
Para entender como os dois tipos de filtro funcionam, é necessário entender o comportamento do capacitor nos dois tipos de circuito. E, podemos utilizar dois tipos de abordagem na explicação: a da reatância capacitiva e a do tempo de carregamento e descarregamento do capacitor.
As duas abordagens são validas para entender o filtro. Embora, a de reatância capacitiva ajude mais a entender a matemática por trás das fórmulas dos filtros.
Abordagem 1 – Reatância capacitiva
Para sinais alternados, o capacitor apresenta uma resistência, chamada de reatância capacitiva (Xc). E ela é dada pela seguinte fórmula:
Onde f é a frequência do sinal e C é a capacitância do capacitor.
A partir da fórmula anterior, podemos fazer uma análise. Considerando o valor de C constante:
Para sinais de baixa frequência (valor de f baixo), o valor de Xc tende a ser alto, e, para sinais de alta frequência (alto valor de f), o valor de Xc tende a ser baixo.
Ou seja, se Xc representa uma resistência, isto quer dizer que o capacitor apresenta uma alta resistência para sinais de baixa frequência. E, isto implica que este tipo de sinal terá dificuldade de passar pelo capacitor. E o contrário acontece, sinais de alta frequência terão maior facilidade de passar pelo capacitor (devido à baixa reatância).
Efeito da reatância capacitiva
O resultado da análise anterior é que, se uma carga for ligada em paralelo com o capacitor (passa baixa), os sinais de alta frequência passarão pelo capacitor e os de baixa frequência passarão pela carga. É uma análise similar a um circuito de dois resistores em paralelo: a corrente circulará em maior intensidade pelo caminho de menor resistência.
No caso do filtro passa alta, como o capacitor está em série com a entrada, somente sinais de alta frequência conseguirão passar pela reatância do capacitor.
As explicações anteriores estão simplificadas, pois não foi definido nenhum referencial para dizer o que é alta frequência e o que é baixa. Mas, no tópico de análise matemática do filtro, veremos sobre a frequência de referência chamada de frequência de corte.
Por fim, você pode fazer o seguinte questionamento: De acordo com a explicação, não é necessário nenhum resistor no circuito do filtro, apenas o capacitor. Você está certo em pensar isto, pois, na realidade, o resistor é um dos parâmetros para definir a frequência de corte e não tem um papel efetivo na filtragem do sinal (me refiro à atenuação).
Abordagem 2 – Tempo de carregamento e descarregamento
Outra abordagem valida para o entendimento dos filtros é por meio do tempo de carregamento e descarregamento do capacitor.
Vamos começar considerando a situação de um sinal de entrada contínuo e constante como o da imagem abaixo. Idealmente, este tipo de sinal possui uma frequência de 0Hz.
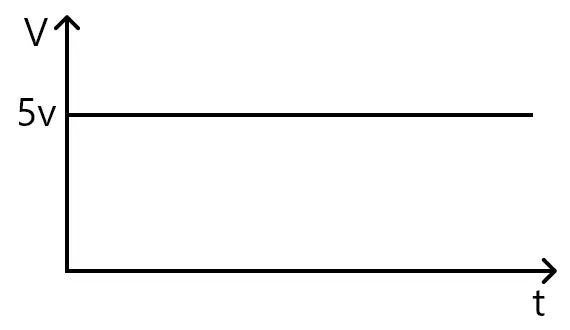
Em determinado momento, o capacitor será carregado pela fonte. E, quando isto ocorre, o capacitor se comporta como uma chave aberta. Ou seja, todo o sinal contínuo é bloqueado pelo capacitor.
Vamos imaginar agora um sinal alternado (frequência diferente de 0) com um capacitor que demora um tempo infinito para carregar e descarregar.
Como a tensão do circuito está sempre alternando, o capacitor ficará carregando e descarregando e nunca ficará carregado. Por conta disto, ele irá se comportar como uma chave fechada (curto).
Efeito do carregamento e descarregamento
A partir das suposições anteriores, podemos relacionar o sinal alternado e o contínuo com sinais de alta e de baixa frequência respectivamente. Portanto, o capacitor impede a passagem de sinais de baixa frequência e facilita a passagem de sinais de alta frequência.
A alta e baixa frequência aqui dependem do valor da capacitância. Por exemplo, um caso em que há um capacitor que demora 1 segundo para carregar e há um sinal de entrada que varia a cada 10 milissegundos.
Neste contexto, o capacitor tem 10 milissegundos para carregar e descarregar, sendo que ele gasta 1 segundo para fazer um dos dois. Ou seja, ele agirá como uma chave fechada (“curto”) possibilitando a passagem do sinal de alta frequência e nunca ficará carregado.
Análise matemática do filtro
Frequência de corte
No início do post, foi citado que os filtros filtram sinais a partir de um frequência de referência, que é conhecida como frequência de corte. Em termos práticos, esta frequência é definida como a frequência em que o sinal sofre uma atenuação de cerca de 30%.
Isto é, na frequência de corte, o sinal de saída possui 70% (aproximado) da intensidade do sinal de entrada. Estes valores de 30% e 70% não são totalmente aleatório, pois eles vêm da análise quando R = Xc (resistor tem mesmo valor da reatância capacitiva).
Quando fazemos o cálculo de um circuito em que R = Xc, a tensão em cima do capacitor é 70,7% da tensão de entrada. No caso do filtro passa-baixa, desta frequência para cima, a intensidade dos sinais cai abaixo de 70%. E, no caso do filtro passa-alta, desta frequência para baixo, a intensidade dos sinais cai abaixo de 70%.
Fórmula da frequência de corte
Com a explicação acima, fica fácil deduzir a fórmula da frequência de corte. Relembrando a fórmula de Xc:
Se R = Xc, então (nesta situação f é a frequência de corte):
Manipulando a equação, temos que:
Portanto, a partir da fórmula acima, você é capaz de encontrar qual é a frequência de corte de um filtro já criado ou projetar um filtro (passa-baixa e passa-alta). Para o primeiro caso, basta inserir os valores de R e C na fórmula e achar a frequência.
Para o caso em que se deseja projetar o filtro, basta estipular um valor para R ou para C e definir qual será a frequência de corte. Por exemplo, estipulando um resistor de 1kΩ e uma frequência de corte de 60Hz, podemos calcular o capacitor:
Se o exemplo acima for um filtro passa-baixa, basta ligar um resistor de 1kΩ em série com o capacitor de 2,65μF e considerar a saída em paralelo com o capacitor. Se for o filtro passa-alta, é só fazer o contrário.
Ganho do sinal
A descrição da atenuação em porcentagem que fiz foi só para facilitar o entendimento da frequência de corte. Entretanto, a filtragem do sinal é descrita em termos de ganho (inverso de atenuação) em uma escala logarítmica (decibéis).
O ganho do sinal é a tensão de saída dividida pela tensão de entrada. Mas o ganho na escala logarítmica é mais complexo e é dado pela seguinte fórmula:
Sendo Vs a tensão de saída e Ve a tensão de entrada.
Para o caso da frequência de corte, em que Vs/Ve = 70,7%, o ganho é cerca de -3dB. Esse valor é importante para a análise gráfica da atenuação.
Gráfico do ganho
Veja abaixo como é o comportamento do ganho de um filtro passa-baixa de acordo com a frequência angular do sinal (2πf).
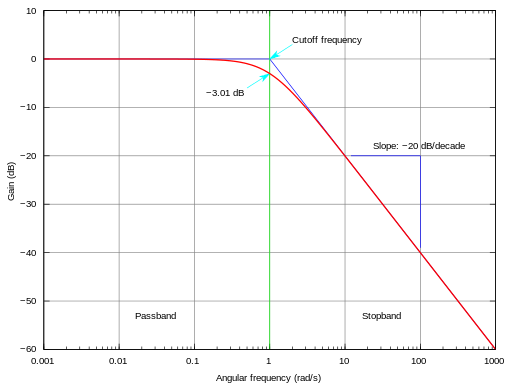
A partir da imagem acima, é possível observar que, o ganho do sinal (em decibéis) de frequências antes da frequência de corte é praticamente 0. Isto implica que frequências abaixo da frequência de corte não são afetadas pelo filtro. Sendo mais preciso, alguns Hertz próximo da frequência de corte, o ganho já começa a diminuir.
E, após a frequência de corte, o ganho diminui 20dB a cada década (potência de 10). No caso do gráfico, alguns hertz depois da frequência de corte, o ganho é -10dB, o que corresponde a uma tensão de saída de apenas 30% da tensão de entrada.
O gráfico do filtro passa-alta é um espelho do gráfico do filtro passa-baixa. Portanto, a inclinação negativa do gráfico está na parte esquerda e a parte constante está na direita. Veja como ele é no primeiro gráfico da imagem abaixo.
A análise é parecida com a anterior: próximo à frequência de corte, a intensidade (magnitude) do sinal começa a diminuir conforme diminuímos a frequência. E ela é constante para frequências um pouco mais altas que a frequência de corte.
Exemplo de aplicação
Se você entende sobre as componentes dos sinais elétricos, é provável que você saiba a utilidade dos filtros capacitivos. Portanto, reforço a importância da leitura do post que aborda este assunto.
Entretanto, para esclarecer melhor a ideia de filtro, vamos analisar algumas aplicações:
Sinal com as duas componentes
Considere um sinal que possui uma componente alternada 10sen(x)V e uma componente contínua 5V, conforme imagem abaixo:
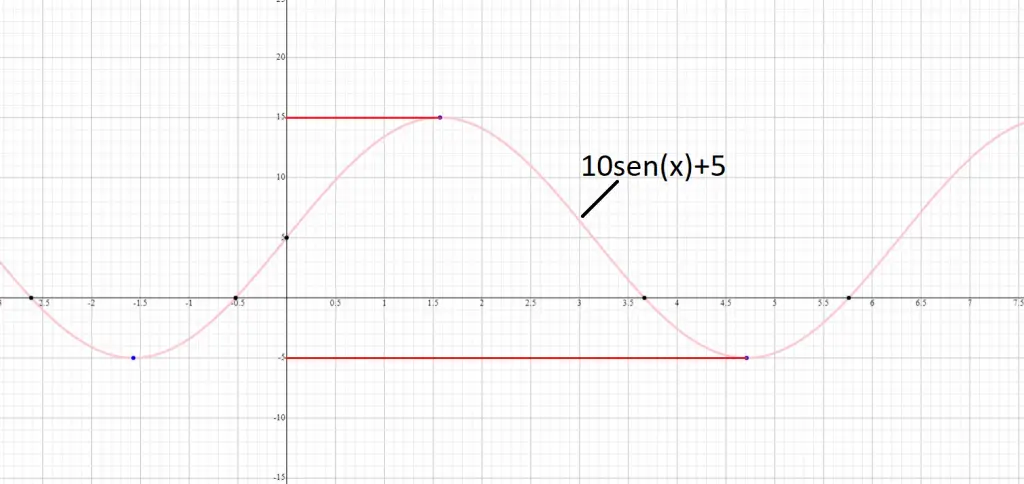
Agora, vamos supor que queremos um filtro para remover o sinal alternado (alta frequência) e um filtro para remover o sinal contínuo (baixa frequência). O primeiro filtro será um passa-baixa e o segundo um passa-alta.
A última informação importante para ter em mente antes de projetar os filtros é que a frequência do sinal contínuo é 0Hz e a do sinal alternado é 1Hz.
Para exemplificar o uso das fórmulas, vou calcular o filtro passa-baixa estipulando o resistor e o passa-alta estipulando o capacitor.
Projetando o filtro passa-baixa
Como o sinal alternado é 1Hz, devo criar um filtro para impedir essa frequência de passar. Se eu fizer a frequência de corte em 1Hz, o sinal alternado irá aparecer na saída com 70% da intensidade.
Porém, o que eu quero, é que ele não apareça. Portanto, vou fazer a frequência de corte ser 0,1Hz, o que gerará uma alta atenuação. O sinal alternado ainda irá aparecer na saída, mas será de baixa magnitude.
Para começar os cálculos, vou estipular um resistor de 1kΩ (poderia também ter estipulado o capacitor). Manipulando a fórmula mostrada anteriormente:
Arredondando, vou utilizar um capacitor de 1500μF.
Projetando o filtro passa-alta
Devo criar um filtro para impedir a frequência de 0Hz de passar, mas que deixe a de 1Hz passar. Portanto, vou considerar uma frequência de corte de 0,5Hz.
Para calcular o filtro, vou estipular um capacitor de 100μF (poderia também ter estipulado o resistor). Manipulando a fórmula mostrada anteriormente:
Arredondando, vou utilizar um resistor de 3000Ω.
Resultado simulado
O circuito dos filtros foi simulado no Multisim e ficou da seguinte forma:
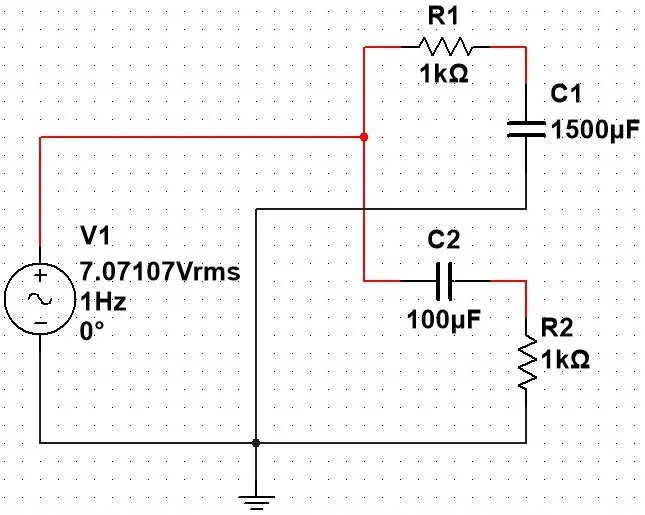
A parte superior do circuito é o filtro passa-baixa (vai deixar passar apenas o sinal contínuo). E a parte inferior é o filtro passa-alta (vai deixar passar apenas o sinal alternado).
A fonte é de 7,07Vrms, mas o pico é de 10V, seguindo o sinal 10sen(x). E ela possui um offset positivo de 5v para simular a parte contínua do sinal. Após simular o circuito, os seguintes resultados foram obtidos (abra as imagens em uma nova guia para ver melhor):
Tensão na saída do filtro passa-baixa:
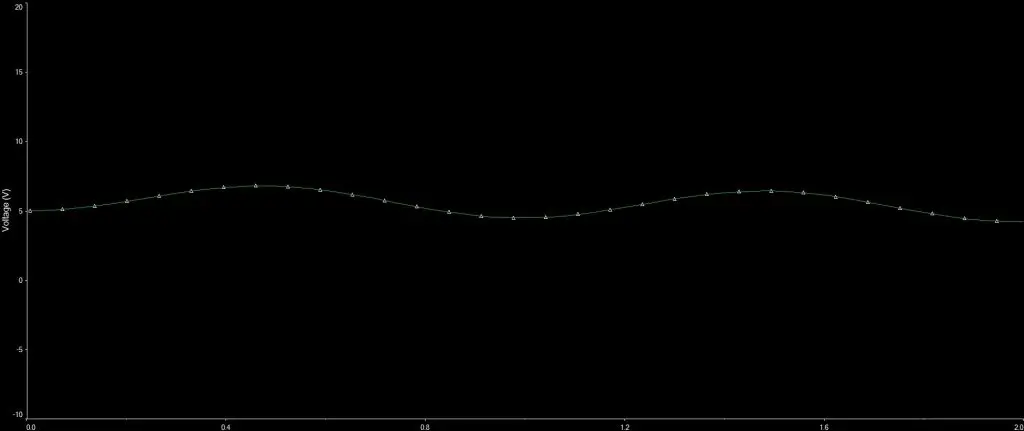
A tensão de saída ficou relativamente constante, apresentando uma oscilação de ~1,2V. Isto quer dizer que a componente alternada ficou com 12% da intensidade original (1,2/10). Se quiséssemos melhorar este filtro, bastaria diminuir a frequência de corte ainda mais.
Tensão na saída do filtro passa-alta:
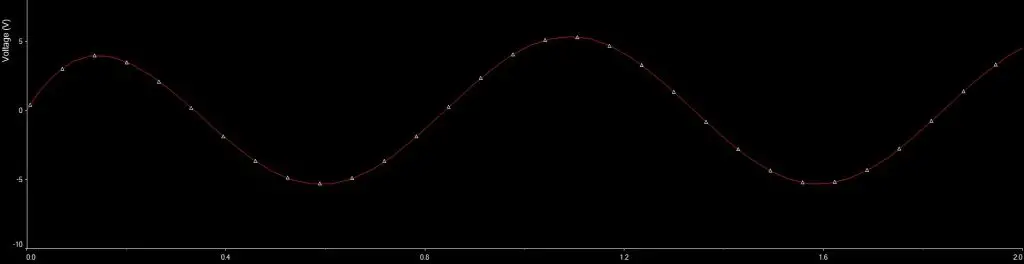
A tensão ficou praticamente puramente alternada, sendo que a tensão de pico positiva ficou pouco acima de 5V. Entretanto, há um problema no sinal, pois a parte alternada deveria ter 10V de pico.
Isso aconteceu porque o filtro também atenuou a intensidade da componente alternada, já que a frequência de corte está muito próxima do sinal alternado (0.5Hz).
Para melhorar este filtro, bastaria diminuir a frequência de corte um pouco mais.
A tensão de entrada (azul) e as duas tensões de saída:
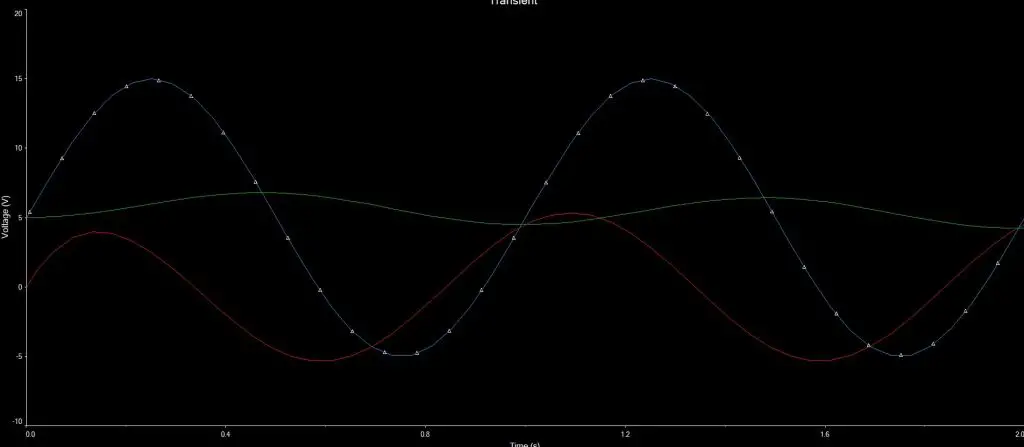
Melhorias nos filtros
Depois deste primeiro resultado, resolvi fazer as melhorias nos filtros conforme dito e diminui a frequência de corte. A diminuição foi feita aumentando o valor do capacitor para 3000μF nos dois casos. Portanto, o circuito dos dois filtros ficou parecido. A nova frequência de corte é 0,053Hz.
E o resultado desta modificação está mostrado abaixo. Em azul está a tensão de entrada. Em verde a do filtro passa-baixa e em vermelho do filtro passa-alta.
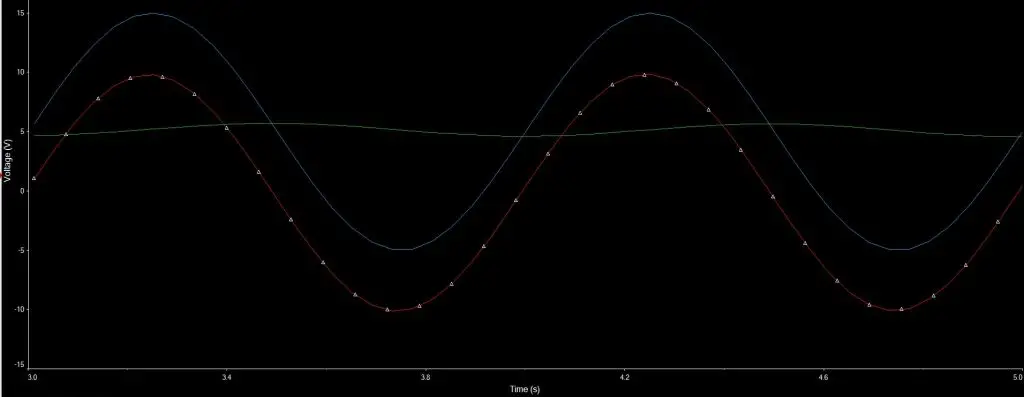
Repare que a tensão de saída do filtro passa-baixa ficou bem mais constante e ficou com uma oscilação mais baixa que anteriormente (agora varia ~0,6V). Houve melhora também na tensão de saída do filtro passa-alta, pois o sinal apresentou uma tensão de pico próxima de 10V e ficou sem componente contínua.
Observação crucial
As análises do exemplo de aplicação permitem ter uma noção boa dos filtros. Mas existe uma situação em que o sinal de saída pode fugir do esperado. Vamos analisá-la.
Imagine que você deseja filtrar um sinal puramente alternado como o da imagem abaixo com um filtro passa baixa.
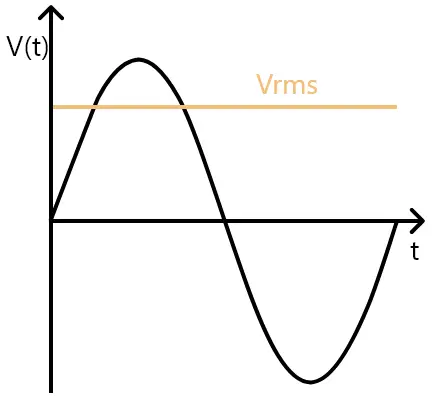
Se você utilizar uma frequência de corte muito abaixo da frequência do sinal, o esperado é que a tensão de saída seja nula. Isto porque a unica componente do sinal é a senoide da figura. Até aí tudo bem. Mas imagine que seu circuito seja o da figura abaixo (a fonte é uma senoide pura).
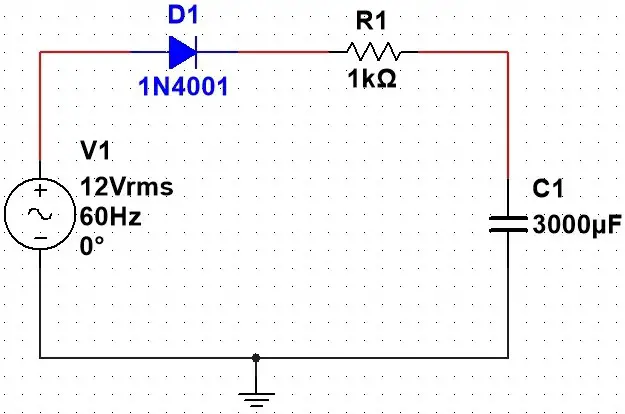
O circuito acima possui uma frequência de corte de 0,05Hz. Portanto, o esperado é que a tensão de saída seja nula (pois o capacitor filtrará a senoide de 60Hz).
Entretanto, o sinal de saída não é igual o esperado. Ele, na realidade, fica contínuo com valor igual ao da tensão de pico do sinal de entrada (em determinado momento após energizar o circuito). Mas como isso acontece se o sinal de entrada não tem nenhuma componente contínua?
O que ocorre é que, no circuito da imagem acima, o capacitor não tem onde descarregar (devido ao diodo). Por conta disto, em todo semiciclo positivo, ele carrega, e, em todo semiciclo negativo, ele mantem a carga constante. Como ele fica carregando constantemente, a tensão em cima dele vai subindo até atingir a tensão de pico da fonte.
Como a constante de carregamento (R*C) do circuito acima é alta (3s), o capacitor demora muito tempo para atingir a tensão de pico. A imagem abaixo mostra a simulação da tensão de saída após 50s. Em vermelho a tensão de saída e em verde a tensão senoidal.
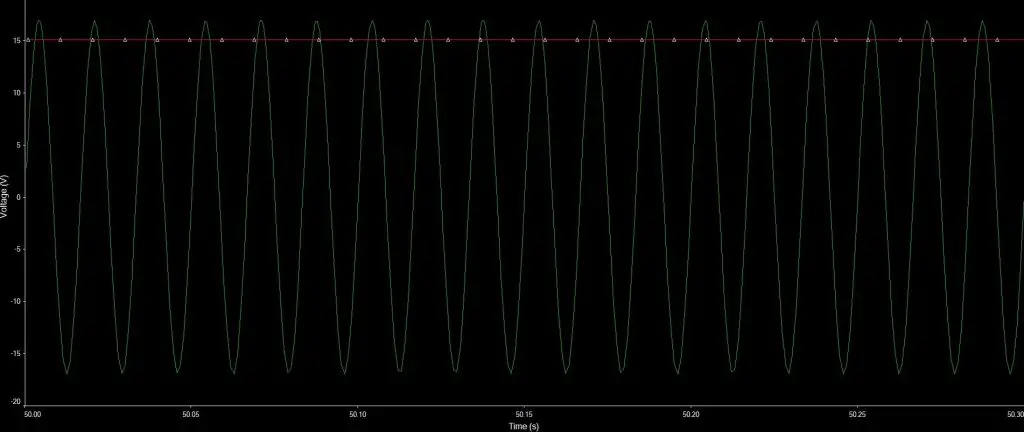
Para resolver este “problema”, basta colocar uma carga em paralelo com o capacitor do filtro. Assim, ele terá onde descarregar e a tensão de saída será mais próxima do esperado: nula.
Ela pode ser diferente se o valor da carga for muito alto. Isso porque o capacitor terá um tempo de descarga muito grande e acontecerá o mesmo da situação acima.
Componentes dos sinais elétricos

Boa noite! Qual seu nome completo? pra eu poder usar nas referências do meu relatório
Boa noite, Edlane! É Fábio Guimarães de Sousa. Fico feliz em saber que o site contribuiu com seu trabalho!
muito bom, se possivel gostaria de saber um pouco mais sobre circuitos em ac . especialmente sobre circutos resonantes rc ou lc , de especial rc ou seja aqueles usados em dimmer de potencia na rede eletrica , tenho certa duvida , na carga do capacitor com o angulo de fase e seu filtro rc . como a potencia e entregue a carga atraves do seu angulo , ao acionador gate
Obrigado pelo comentário, Reginaldo! Anotei sua sugestão e vou avaliar a ideia de escrever um post sobre estes assuntos. Em relação ao dimmer, tem um post aqui no site que explica um circuito possível. Outro tipo de circuito RC que você poder ler aqui no site seria no post sobre o multivibrador astável. E você comentou sobre acionar o gate, mas não entendi muito bem qual seria o tipo de circuito que você está se referindo.
Ótima aula.
Muito obrigado, Fernando!
Esse circuito funciona como passa baixa para sub. Gostaria de um circuito simples passa baixa grato pela atenção
Olá, Marlon. Acredito que não seja muito adequado, mas não posso te dar certeza, pois não tenho experiência prática com o assunto. Talvez uma melhor solução seja utilizando um filtro ativo com amplificador operacional. Se você pesquisar “filtro passa baixa para subwoofer” no Google, encontrará diversos circuitinhos prontos que parecem funcionar bem para este propósito.
Gostaria de informação para fazer um circuito passa baixa
Aquilo que o homem ignora não existe para ele, por isso o universo de cada um se resume ao tamanho do seu saber.
Muito bem dito, Valério.
gostei da aula aprendi bastante em pouco tempo
bem explicada a sua aula
Show de bola, João! Espero que também goste dos outros conteúdos do site.