O controle PID é uma ótima ferramenta para controle de processos industriais e também no controle de robôs. Sendo assim, vamos aprender a implementá-lo na prática e entender as diferenças entre os controladores P, I, D e suas combinações.

Informações básicas

A teoria de controle por trás dos controladores P, I e D é bem densa e complicada. Por conta disso e pelo fato de minha formação não ser voltada para controle, não pretendo entrar nos mínimos detalhes. Minha intenção é trazer uma visão mais prática e mostrar as diferenças entre os controladores P, I, D, PI, PD e PID.

Também não pretendo entrar nos conceitos de malha de controle, porque o objetivo é apresentar uma explicação superficial para qualquer um conseguir entender de forma direta.

Contextos

Antes de explicar o que é um controlador, vejamos alguns contextos em que ele está inserido.

Imagine que você deseja controlar a temperatura de um quarto automaticamente. Nesse caso, a temperatura seria o parâmetro a ser controlado, também chamada de variável controlada. E, para garantir que o controle dela seja possível, seriam necessários elementos para medir a temperatura do ambiente e para atuar no ambiente (sensores e atuadores). Claro, é preciso também de um ou mais elementos para ler os sensores, processar os dados e comandar os atuadores. Todos estes elementos combinados constituem o sistema de controle automático da temperatura do quarto. Por exemplo, poderíamos ter um sensor de temperatura, um aquecedor e um computador que lê o sensor, processa os dados e comanda o aquecedor.

Outro cenário seria o controle automático do nível de um líquido de um tanque industrial. Nesse sentido, o nível seria a variável controlada e o sistema seria constituído por: medidor de nível, válvulas de entrada e saída do tanque e o elemento que processa e controla o nível.

Enfim, o importante é entender os conceitos de sistema e de variável controlada, pois os controladores (que fazem parte do sistema) servem justamente para controlar a variável controlada (redundante, mas achei necessário deixar claro). O centro do problema é a diminuição da diferença que pode existir entre o valor desejado e o valor da medição, diferença esta chamada de erro.

O que é um controlador

Diante do que foi falado acima, o controlador é uma técnica/ferramenta para controlar um determinado parâmetro de um sistema. E, por controlar, presume-se que o controlador é capaz de conduzir e manter o sistema em um estado desejado. Para isso, o erro entre o valor desejado para o parâmetro e o valor medido deve ser o menor possível.

Como ele é uma técnica/ferramenta, não existe um formato único em que ele aparece. Isto é, é possível construir um controlador por meio de circuitos analógicos ou digitais, ou por meio de firmware/software. No caso deste post, criaremos os controladores via software.

Outro ponto importante de mencionar é que os controladores P, I, D, PD, PI e PID não são os únicos possíveis de serem utilizados. Além deles, pode-se utilizar, por exemplo, a lógica fuzzy, algoritmos com redes neurais artificiais ou até controladores com regras arbitrárias. Um exemplo é este post onde criei um circuito digital para controle de um tanque de água utilizando regras simples. Entretanto, o controlador PID (em específico) é relativamente simples de implementar e atende bem muitos processos.

Obtenção dos parâmetros ótimos dos controladores

Gostaria de deixar claro que não pretendo mostrar como obter os parâmetros ótimos dos controladores. Nos testes que fiz, os parâmetros foram obtidos por meio de tentativa e erro.

Cenário de simulação (desenvolvido em Python)

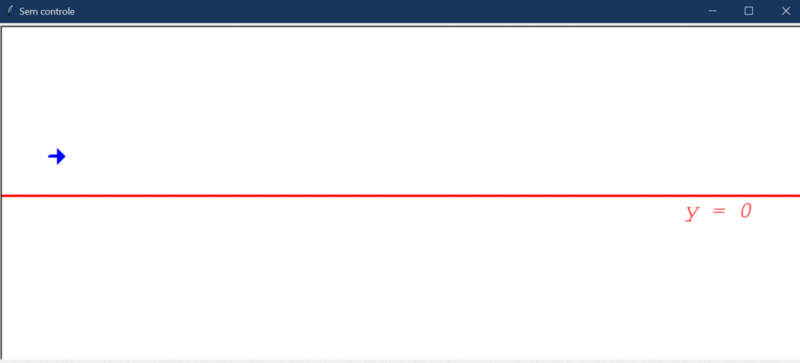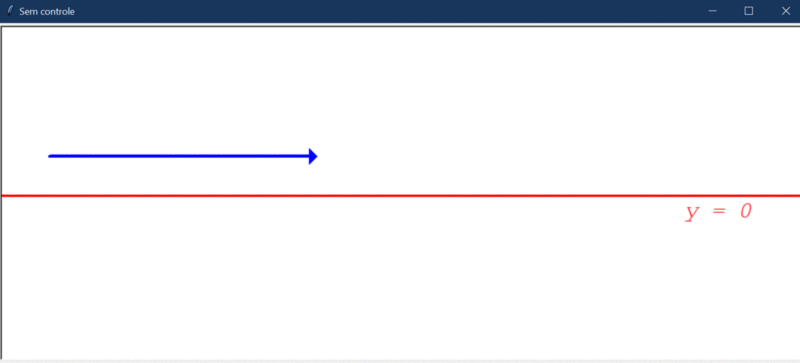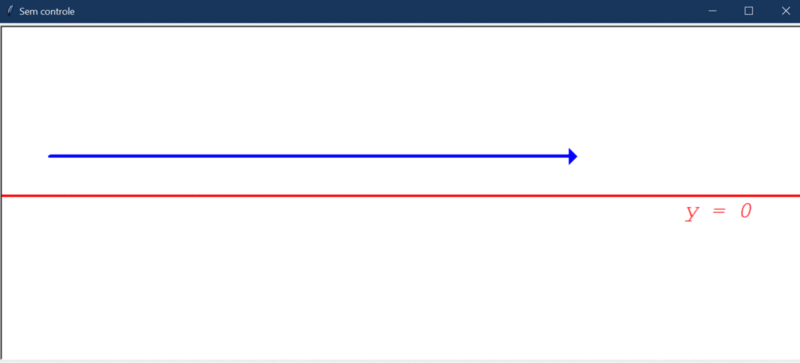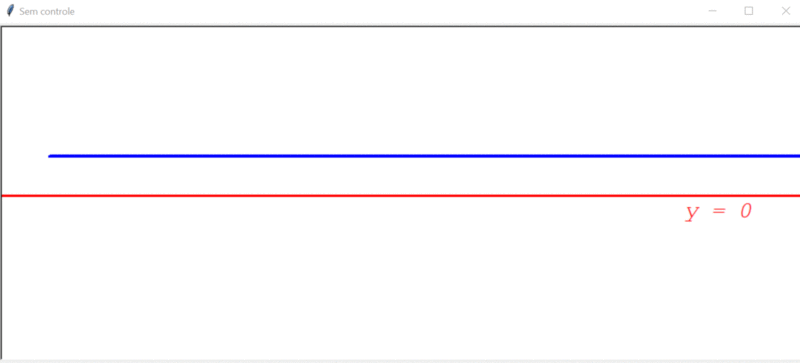
Para explicar e mostrar o funcionamento dos controladores P, I, D, PD, PI e PID na prática, criei um cenário com um robô localizado em um plano cartesiano. Esse robô sempre anda para frente 10 unidades e gira x graus em alguma direção (esquerda ou direita). O objetivo aqui é criar um controlador para fazer o robô andar ao longo do eixo y (y=0). Ou seja, o robô deve andar em linha reta ao longo do eixo y do plano cartesiano.

Obs1: O robô sempre começa na coordenada (-450, 50).

Obs2: tirei a ideia deste controlador de um curso gratuito de robótica que fiz na Udacity.

Código base

Adiante está o código base que usarei para os testes. Por conta disso, adicionei comentários explicando cada parte. Recomendo ler com calma, pois removerei os comentários nos códigos dos testes.

Repare que a única forma de controlar o robô é variando o ângulo que ele deve girar ao mover, pois ele sempre anda 10 unidades para frente.

A classe robo eu criei em um arquivo separado (auxiliar.py) e ela contém a parte complicada do código (veja o tópico seguinte).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Biblioteca com a parte complexa do código
import auxiliar

# Instancia do robô ("Sem controle" é o título da janela)
robo = auxiliar.Robo("Sem controle")

# Quantidade de movimentos que o robô realiza
STEPS = 120
for i in range(STEPS):
    # Como a posição desejada é y = 0,
    # o erro será a posição do robo - 0
    # que é igual à própria posição
    erro = robo.getYPos()
   
    controle = 0

    # Move o robô 10 unidades e gira ele x graus, onde x = controle
    robo.move(controle)

# Plota a evolução do erro ao longo dos movimentos
robo.plotError()
robo.end()

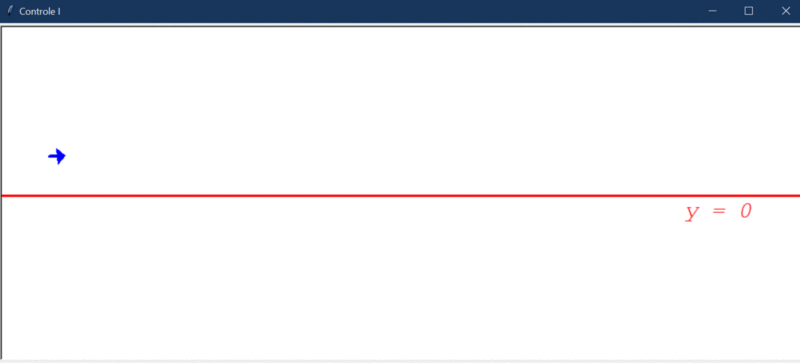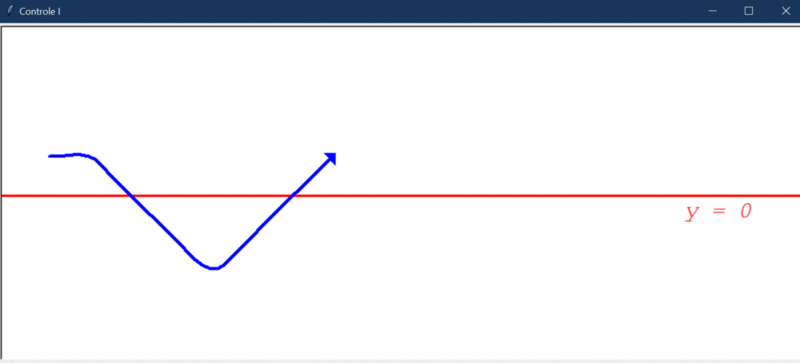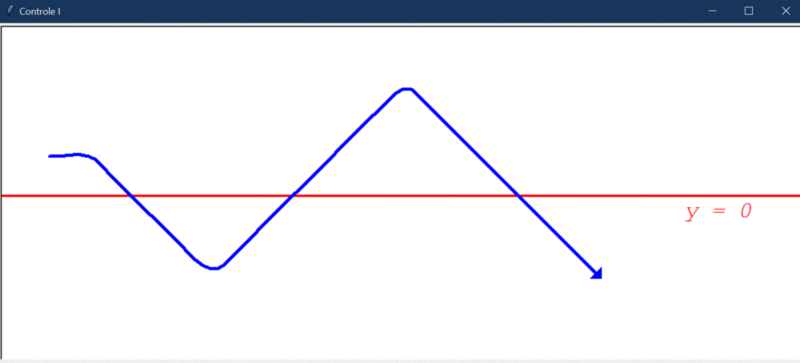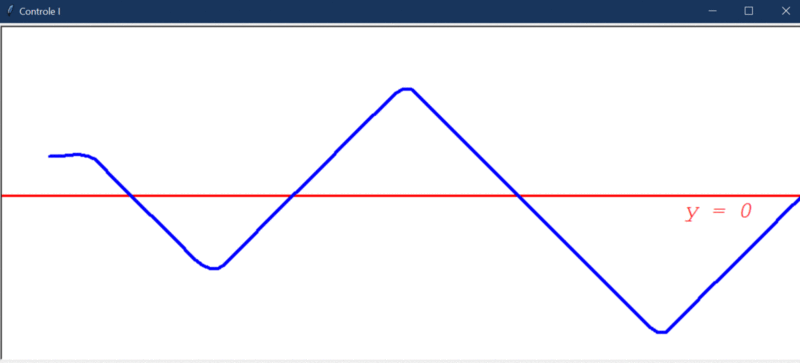
Após rodar o código acima (que não contém nenhum controlador), o robô apenas anda reto:

Robô sem controle

Disturbio

É possível criar o robô adicionando um distúrbio em sua rotação instanciando ele da seguinte forma:

robo = auxiliar.robo(“Sem controle”, disturbio = 10)

Esse distúrbio simula o caso onde uma roda do robô se movimenta mais que a outra ocasionando uma rotação adicional indesejada. Como na vida real nada é perfeito, sempre vai existir um distúrbio nos sistemas, e observar seu impacto nos controladores é bem importante. Em alguns sistemas, o distúrbio vai ser bem pequeno ou imperceptível e, nos testes, eu irei exagerar para podermos observar nitidamente os efeitos que ele provoca.

Código auxiliar

Resolvi criar esse código à parte para você poder concentrar nas técnicas, mas, se quiser entendê-lo, saiba que ele se baseia na utilização da biblioteca turtle para a parte da animação e movimentação do robô. Se você for testar os códigos do post, salve o código abaixo com o nome “auxiliar.py” na mesma pasta que o restante dos códigos.

Obs: você vai precisar de instalar a biblioteca matplotlib (pip install matplotlib).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
import turtle
import matplotlib.pyplot as plt

class Robo():
    def __init__(self, name = "Controle", speed = 0, disturbio = 0):
        '''Inicializa a instancia

            Args:
                name: nome dado a janela do 'turtle'
                speed: velocidade da instancia do 'turtle'
                        0 = velocidade máxima
                disturbio: disturbio no ângulo ao movimentar (em graus)
                            angulo final = rotação + disturbio
        '''
        # Configura a tela do turtle
        self.win = turtle.Screen()
        self.win.setup(0.4, 0.3)
        self.win.bgcolor('white')
        self.win.title(name)

        # Cria a linha vermelha de referência
        turtle.hideturtle()
        turtle.pensize(3)
        turtle.speed(0)
        turtle.color('red')
        turtle.goto(-800, 0)
        turtle.forward(1600)

        turtle.penup()
        turtle.goto(400,-36)
        turtle.write('y = 0', font=('Courier', 22, 'italic'), align='center')

        # Configura o robo
        self.robo = turtle.Turtle()
        self.robo.hideturtle()
        self.robo.pensize(4)
        self.robo.shape('arrow')
        self.robo.color('blue')
        self.robo.resizemode('user')
        #robo.shapesize(0.3, 0.3, 0.3)
        self.robo.speed(speed)

        # Coloca o robo na posição inicial
        self.robo.penup()
        self.robo.goto(-450, 50)
        self.robo.showturtle()
        self.robo.pendown()

        #Acompanha o angulodo robô
        self.angle = 0

        # Lista para plotar erro
        self.erro_list = []

        # Disturbio natural na medição da direção
        self.disturbio = disturbio

        self.counter = 1

    def getYPos(self):
        '''Retorna a posição Y do robô
        '''
        return self.robo.ycor()


    def move(self, turn, distance = 10):
        '''Move o robô em uma direção considerando
           a mudança no ângulo e a distância

           Args:
               turn: ângulo que o robô deve rotacionar para movimentar
               distance: distancia que o robô deve andar
        '''
        # Obtem o novo valor do ângulo considerando o
        # erro e o disturbio
        new_angle = turn + self.disturbio

        # Muda a direção e anda
        self.robo.forward(distance)

        if new_angle < 0:
            self.robo.right(abs(new_angle))
        else:
            self.robo.left(new_angle)

        self.angle += new_angle

        # Limita o movimento em +-45º
        if(self.angle > 45):
            self.angle = 45
            self.robo.setheading(45)
        elif(self.angle < -45):
            self.angle = -45
            self.robo.setheading(-45)

        # Adiciona o erro atual à lista
        self.erro_list.append(self.getYPos())


    def plotError(self):
        '''Plota a curva do erro em função dos passos
        '''
        plt.xlabel("Passos")
        plt.ylabel("Erro")
        plt.plot(self.erro_list)
        plt.title("Evolução do erro")
        plt.show()


    def end(self):
        turtle.done()

Síntese dos resultados

O vídeo abaixo é uma síntese de alguns resultados obtidos (sem distúrbios).

Controlador proporcional (ou controlador P)

O controlador P é um tipo de controlador que atua na variável controlada de forma proporcional ao erro (como o nome sugere). Isto é, se o erro é pequeno, ele atua pouco na variável controlada e, se o erro é grande, ele atua muito.

No exemplo do robô no plano cartesiano, quanto mais distante o robô está do eixo Y (y=0), maior será o erro, consequentemente, maior será a atuação do controlador proporcional.

Fórmula

Diante do mencionado acima, o controlador proporcional segue a seguinte fórmula:

controlador = erro * GANHO_P

O GANHO_P é um parâmetro que multiplica o erro, e seu valor ideal varia de sistema para sistema. Ele serve para calibrar o controlador para que ele não gere uma resposta brusca (mudança grande) ou imperceptível (mudança pequena).

Enfim, como só controlamos o ângulo que o robô deve virar, quanto maior o erro, maior será o ângulo que o robô irá girar em direção ao eixo Y.

Código completo

Para testar o controlador, realizei 2 testes: 1 normal e outro adicionando um distúrbio de 10º no movimento do robô.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import auxiliar

# 1º teste - Sem disturbio
robo = auxiliar.Robo("Controle P")
# 2º teste - Disturbio de 10º
#robo = auxiliar.Robo("Controle P", disturbio = 10)

GANHO_P = 0.5

STEPS = 120
for i in range(STEPS):
    erro = robo.getYPos()
    # Adiciona-se um 'menos' abaixo, pois um erro positivo = girar ângulo negativo
    controle = - erro * GANHO_P

    robo.move(controle)

robo.plotError()
robo.end()

Características do controlador proporcional

Antes de entrar nos resultados dos testes, vejamos algumas características deste controlador, extraídas da teoria de controle:

  1. Atua no regime transitório e regime permanente do sistema. Isto é, ele tem efeito quando o sistema sai do ponto de partida e vai até o valor desejado (transitório) e também quando o sistema apresenta pouca ou nenhuma variação (regime permanente).
    • Entretanto, ele tem mais efeito no regime transitório, pois, é comum que o regime permanente apresente um erro pequeno.
  2. O controle P não garante erro 0 no regime permanente.
    • Na prática, isto quer dizer que, se o sistema apresentar algum distúrbio, o controlador P não é capaz de levar o erro a 0.
  3. Aumentar o ganho (GANHO_P), normalmente, deixa a resposta do sistema mais rápida e diminui o erro, mas aumentar demais pode deixar o sistema instável por forçar o sistema a trabalhar em saturação (atua apenas em nível máximo ou mínimo).

Resultados

Primeiro, uma observação importantíssima dos testes: a simulação criada é naturalmente instável. Isso significa que o controlador proporcional por si só não é capaz de chegar a um estado onde o erro é próximo de zero. Assim, o “regime permanente” nesse caso pode ser interpretado como um regime onde o movimento do robô se repete de forma cíclica (fica oscilando).

Após rodar o primeiro teste, este foi o resultado obtido:

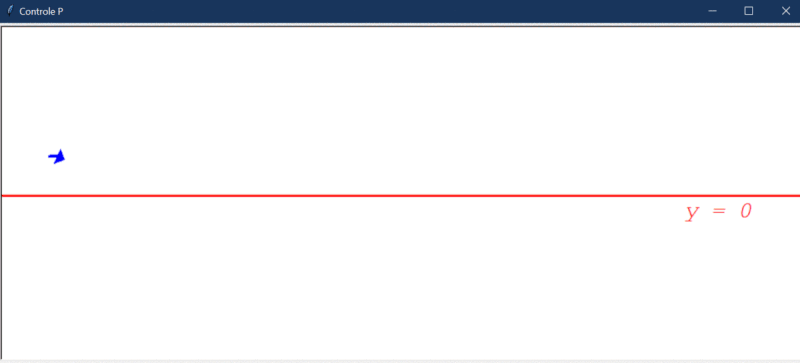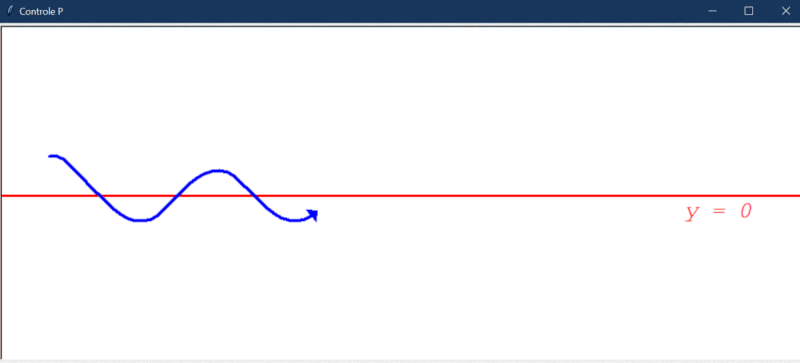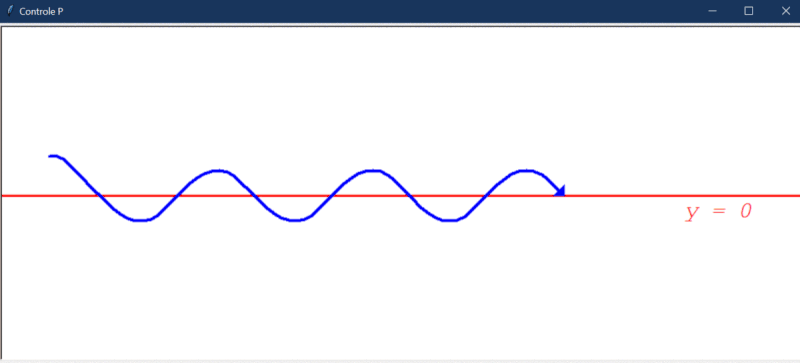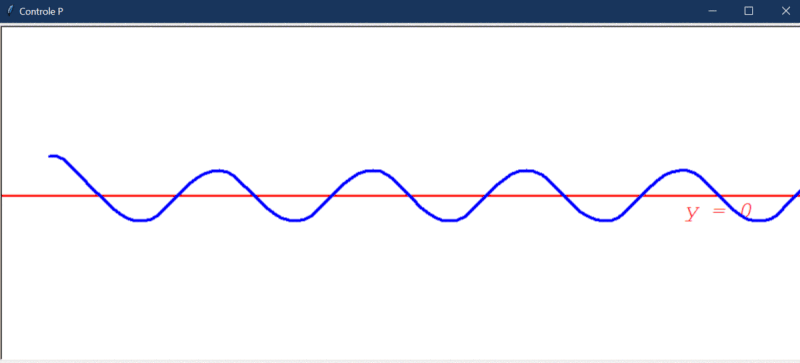
Controlador proporcional

Algumas observações cabíveis:

  • O controlador proporcional é capaz de direcionar o robô a um estado de menor erro, mas, por conta da instabilidade natural do sistema, ele não consegue manter esse estado.
  • Em outros cenários, é totalmente possível que o controlador P sozinho seja capaz de levar o erro a 0.
    • O controle P por si só não garante erro 0, mas num sistema ideal sem distúrbios, é possível que isso ocorra.

Vejamos agora o resultado do teste com distúrbio:

Controlador proporcional com distúrbio

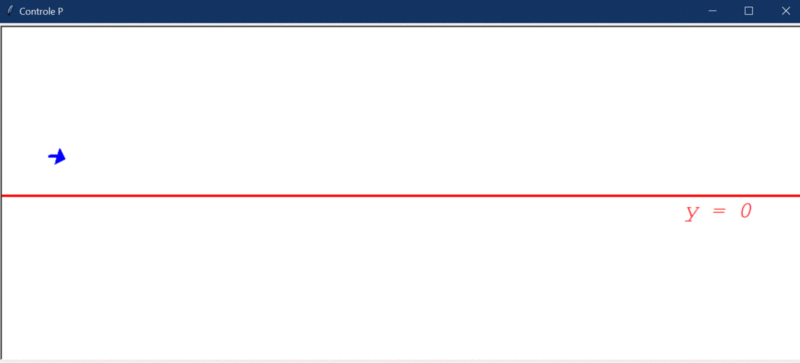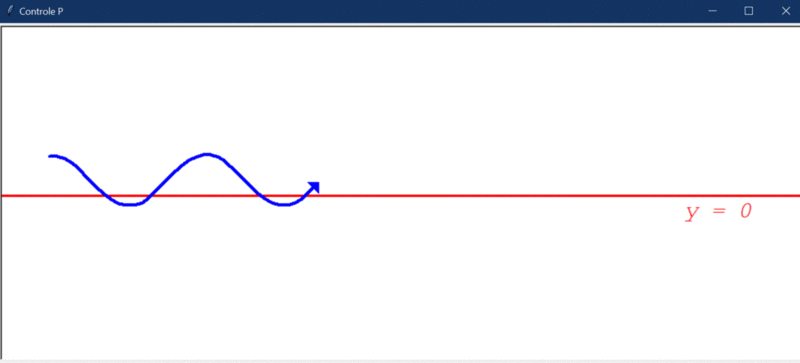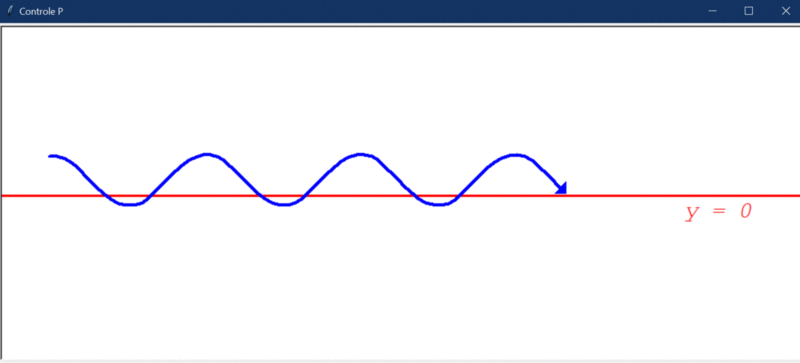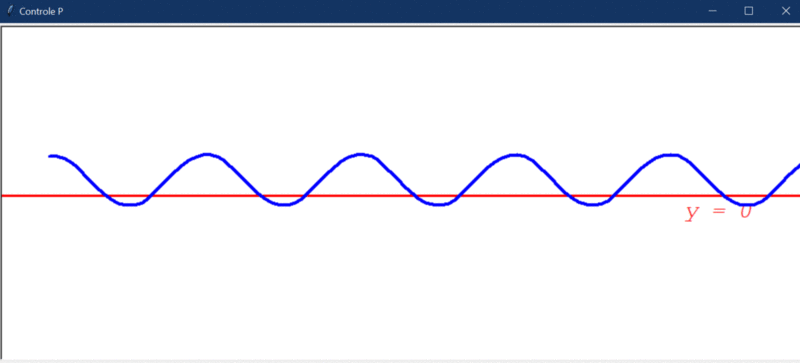
As mesmas observações anteriores são cabíveis, mas repare que agora o sistema não oscila mais ao redor de y=0. Esse é um significado prático do porquê o controlador P por si só não garante erro 0 (ele não elimina “offsets”). No controlador seguinte você entenderá isso melhor.

Controlador integral (ou controlador I)

O controlador I é um tipo de controlador que atua na variável controlada a partir do erro acumulado. Isto é, o erro vai sendo somado (por isso o nome integral) e o controlador usa essa soma para atuar no sistema.

No exemplo do robô no plano cartesiano, quanto mais tempo o robô passar longe de Y=0, maior será o erro acumulado e, consequentemente, maior será a soma. Entretanto, quando o robô passar por Y=0, ainda haverá um erro acumulado que vai diminuindo aos poucos. Isso faz o robô passar direto por Y=0 e ele demora a corrigir a direção do movimento.

Fórmulas

Diante do mencionado acima, o controlador integral segue as seguintes fórmulas:

Inicializa com erro_acumulado = 0

erro_acumulado = erro_acumulado + erro

controlador = erro_acumulado * GANHO_I

O GANHO_I é um parâmetro que multiplica o erro_acumulado, e seu valor ideal varia de sistema para sistema. Ele serve para calibrar o controlador para que ele não gere uma resposta brusca (mudança grande) ou imperceptível (mudança pequena).

Código completo

Para testar o controlador, realizei 2 testes: 1 normal e outro adicionando um distúrbio de 10º no movimento do robô.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import auxiliar

# 1º teste - Sem disturbio
robo = auxiliar.Robo("Controle I")
# 2º teste - Disturbio de 10º
#robo = auxiliar.Robo("Controle I", disturbio = 10)

GANHO_I = 0.1
erro_acumulado = 0

STEPS = 120
for i in range(STEPS):
    erro_acumulado += robo.getYPos()

    # Adiciona-se um 'menos' abaixo, pois um erro positivo = girar ângulo negativo
    controle = - erro_acumulado * GANHO_I
   
    robo.move(controle)

robo.plotError()
robo.end()

Características do controlador integral

Antes de entrar nos resultados dos testes, vejamos algumas características deste controlador, extraídas da teoria de controle:

  1. Atua no regime transitório e regime permanente do sistema.
    • Entretanto, ele tem mais efeito no regime permanente, pois o erro vai sendo acumulado infinitamente.
  2. O controle I garante erro 0 no regime permanente.
    • Na prática, isso quer dizer que o controlador I é capaz de levar o erro a 0 mesmo se o sistema apresentar algum distúrbio.
    • Não é necessariamente verdade em sistemas instáveis (como é o caso das simulações feitas).
  3. Deixa o sistema mais lento e oscilatório.
    • O erro pode demorar a acumular ou “desacumular”, gerando um atraso na resposta do sistema. Também podem aparecer oscilações na resposta mesmo se o sistema for estável.
  4. Aumentar o ganho (GANHO_I), normalmente, deixa a resposta do sistema mais rápida, mas aumentar demais pode deixar o sistema mais oscilatório por gerar um erro acumulado maior e possivelmente levar o sistema a saturação.

Resultados

Após rodar o primeiro teste, este foi o resultado obtido:

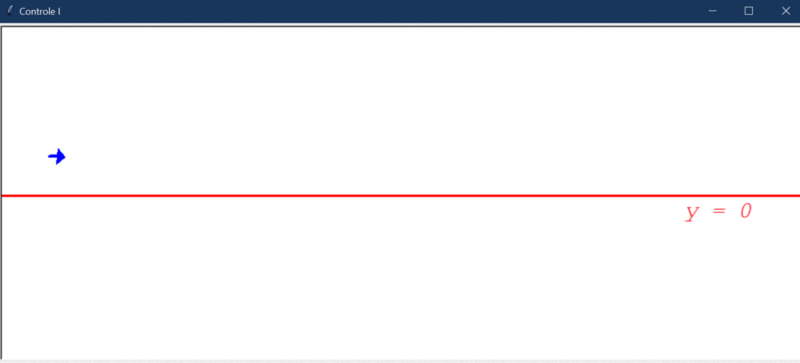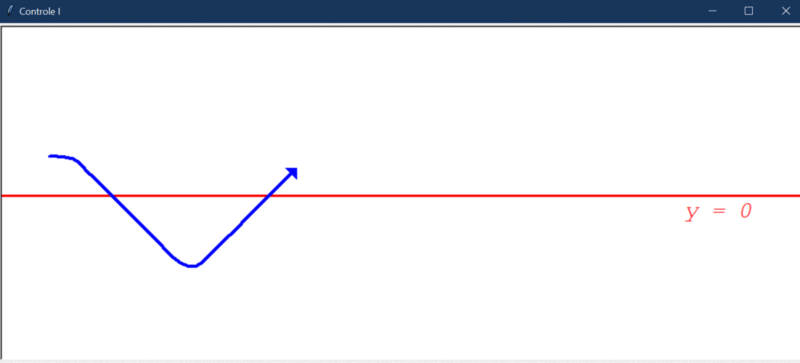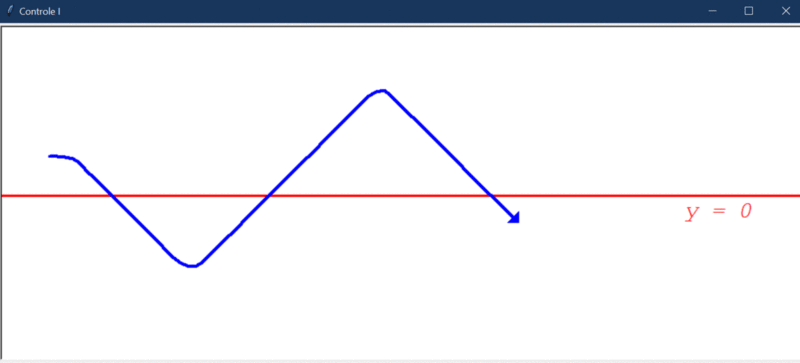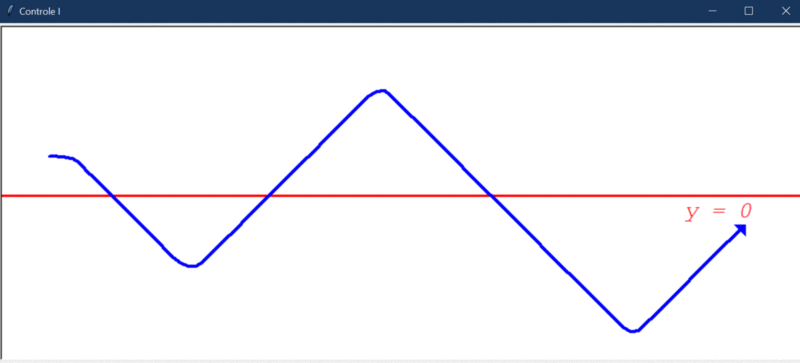
Controlador integral

Algumas observações cabíveis:

  • O controlador integral é capaz de direcionar o robô a um estado de menor erro, mas, por conta da instabilidade natural do sistema, ele não consegue levar e manter o erro em 0.
  • Em outros cenários, é totalmente possível que o controlador I sozinho seja capaz de levar o erro a 0 mesmo com distúrbios.

Vejamos agora o resultado do teste com distúrbio:

Controlador integral com distúrbio

O resultado é praticamente igual ao do teste 1, pois o controlador I conseguiu eliminar o efeito do distúrbio (removeu o “offset”). Isso ficará mais evidente no controlador PI que veremos mais a frente.

Controlador derivativo (ou controlador D)

O controlador D é um tipo de controlador que atua na variável controlada a partir da variação do erro (por isso o nome derivativo). Isto é, ele considera a diferença entre o erro atual e o erro anterior.

Como ele considera a diferença, se ocorrer dela ser 0 (por acaso), o controlador não produzirá nenhum efeito na variável controlada. Isso pode acontecer antes do sistema chegar no ponto desejado, o que faz o sistema “estagnar” e o erro em regime permanente fica bem diferente de 0.

Fórmulas

Diante do mencionado acima, o controlador derivativo segue as seguintes fórmulas:

Inicializa com erro_anterior = 0

erro_diferenca = erro_atual – erro_anterior

controlador = erro_diferenca * GANHO_D

O GANHO_D é um parâmetro que multiplica o erro_diferenca, e seu valor ideal varia de sistema para sistema. Ele serve para calibrar o controlador para que ele não gere uma resposta brusca (mudança grande) ou imperceptível (mudança pequena).

Código completo

Para testar o controlador, realizei 2 testes: 1 normal e outro adicionando um distúrbio de 0.2º no movimento do robô.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import auxiliar

# 1º teste - Sem disturbio
robo = auxiliar.Robo("Controle D")
# 2º teste - Disturbio de 0.2º
#robo = auxiliar.Robo("Controle D", disturbio = 0.2)

GANHO_D = 0.8
erro = 0

STEPS = 120
for i in range(STEPS):
    erro_diferenca = robo.getYPos() - erro
    erro = robo.getYPos()

    # Adiciona-se um 'menos' abaixo, pois um erro positivo = girar ângulo negativo
    controle = - erro_diferenca * GANHO_D
   
    robo.move(controle)

robo.plotError()
robo.end()

Características do controlador derivativo

Antes de entrar nos resultados dos testes, vejamos algumas características deste controlador, extraídas da teoria de controle:

  1. Atua apenas no regime transitório do sistema.
    • Isso, porque o regime permanente pressupõe pouca ou nenhuma variação.
  2. Não garante erro 0 no regime permanente.
    • Na prática, isso quer dizer que o controlador D não é capaz de levar o erro a 0 se o sistema apresentar algum distúrbio.
  3. Dependendo do sistema, o controle derivativo pode melhorar a estabilidade (o caso dos testes realizados).
  4. Aumentar o ganho (GANHO_D), normalmente, deixa a resposta do sistema mais rápida, mas um aumento excessivo pode deixar o sistema oscilatório.

Resultados

Após rodar o primeiro teste, este foi o resultado obtido:

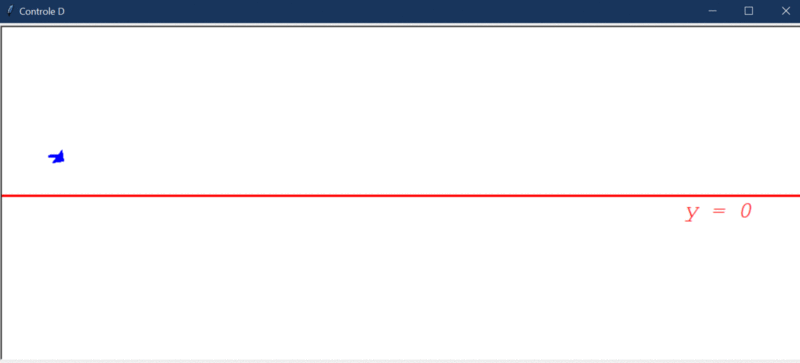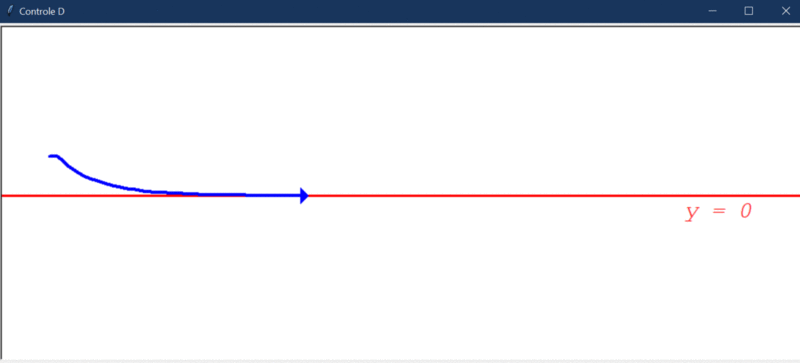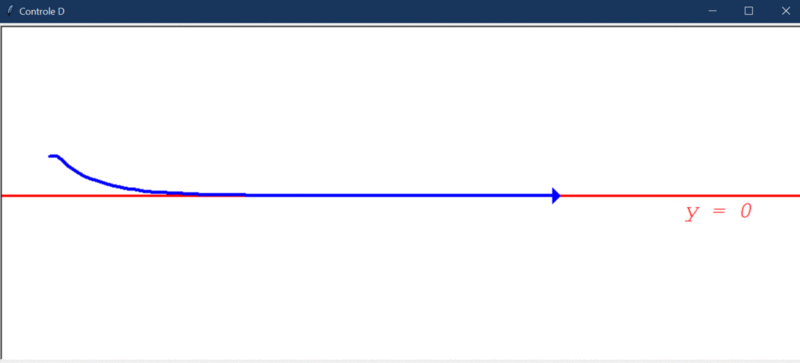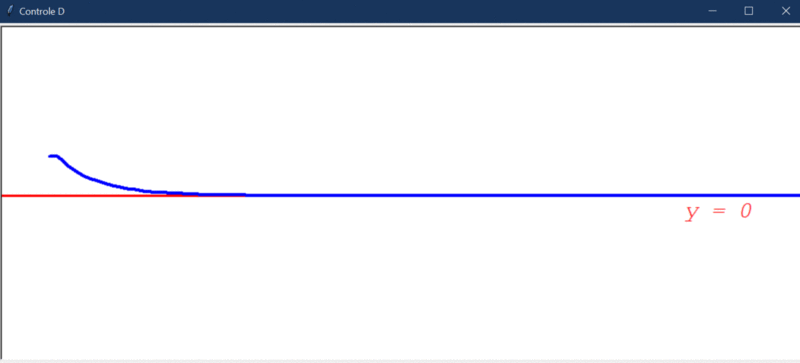
Controlador derivativo

Algumas observações cabíveis:

  • O controlador derivativo foi capaz de deixar o sistema estável, o que não foi observado nos dois casos anteriores.
  • Conseguiu direcionar o robô a um estado de menor erro, mas, ainda assim, o erro em regime permanente não é 0 (é cerca de 0,004).

Aparentemente, o controlador D parece ser perfeito, mas vejamos agora como ele se comporta com a adição do distúrbio, que é bem pequeno (0.2º):

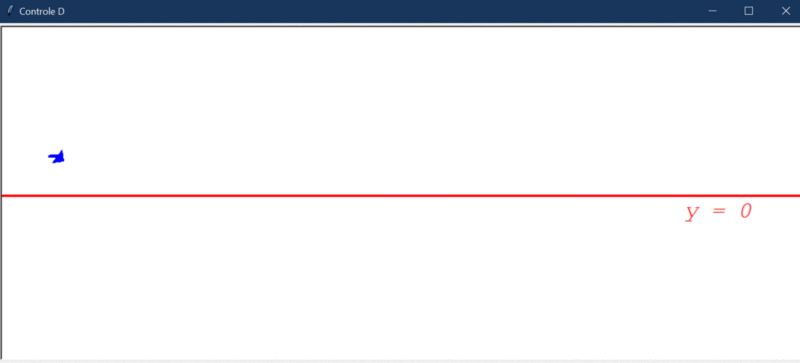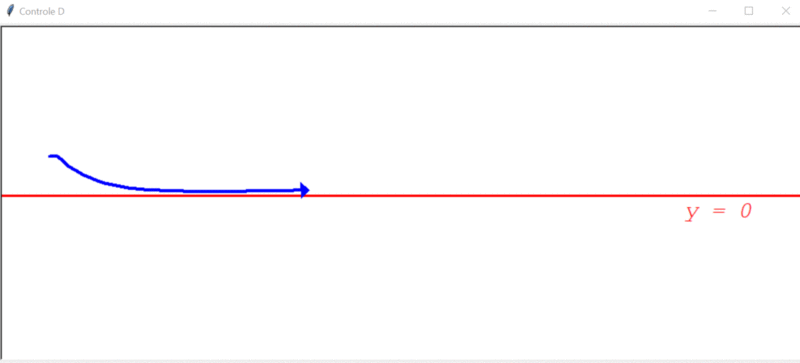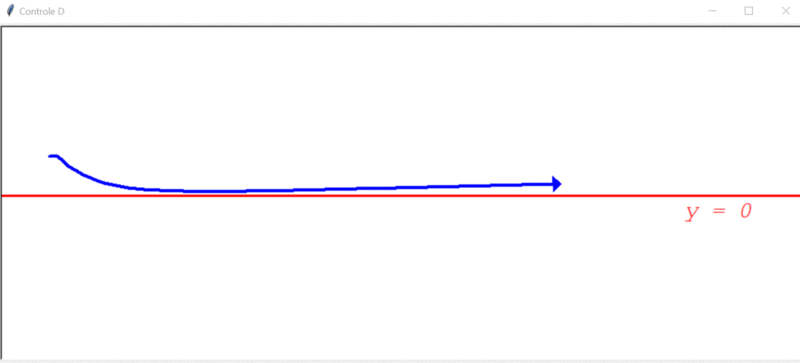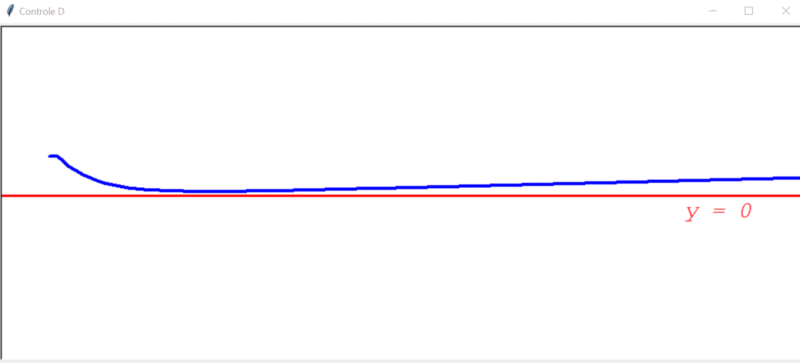
Controlador derivativo com distúrbio

Apesar do erro diminuir no princípio, ele cresce de forma indefinida em um determinado ponto. Isso acontece, porque o distúrbio é constante, ocasionando um erro também constante em um determinado ponto. E, se o erro é fixo, não tem variação e o controlador D não consegue atuar. Ou seja, o controlador D sozinho ainda não resolve todos os problemas.

Controlador proporcional integral (ou controlador PI)

O controlador PI combina os controladores P e I em um só. Portanto, algumas vantagens e desvantagens são compartilhadas.

Fórmulas

Diante do mencionado acima, o controlador PI segue as seguintes fórmulas:

Inicializa com erro_acumulado = 0

erro_acumulado = erro_acumulado + erro

controlador = erro * GANHO_P + erro_acumulado * GANHO_I

Os parâmetros GANHO_P e GANHO_I são os mesmos de antes. Embora os valores acima estejam sendo somados, no código completo eles estão invertidos por conta do motivo de antes (erro positivo = girar o robô com ângulo negativo).

Código completo

Para testar o controlador, realizei 2 testes: 1 normal e outro adicionando um distúrbio de 10º no movimento do robô.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import auxiliar

# 1º teste - Sem disturbio
robo = auxiliar.Robo("Controle PI")
# 2º teste - Disturbio de 10º
#robo = auxiliar.Robo("Controle PI", disturbio = 10)

GANHO_P = 0.5
GANHO_I = 0.01

erro_acumulado = 0

STEPS = 120
for i in range(STEPS):        
    erro = robo.getYPos()
    erro_acumulado += erro
   
    controle = - erro * GANHO_P \
               - erro_acumulado * GANHO_I

    robo.move(controle)

robo.plotError()
robo.end()

Características do controlador PI

Conforme dito anteriormente, este controlador combina característica do controle P e I:

  1. Atua efetivamente no regime transitório (por conta do P) e regime permanente do sistema (por conta do I).
  2. Garante erro 0 no regime permanente (por conta do I).
    • Não é necessariamente verdade em sistemas instáveis (como é o caso das simulações feitas).
  3. Deixa o sistema mais lento e oscilatório (por conta do I).
  4. Normalmente, aumentar o GANHO_P ou diminuir o GANHO_I faz com que o sistema fique mais rápido.

Resultados

Após rodar o primeiro teste, este foi o resultado obtido:

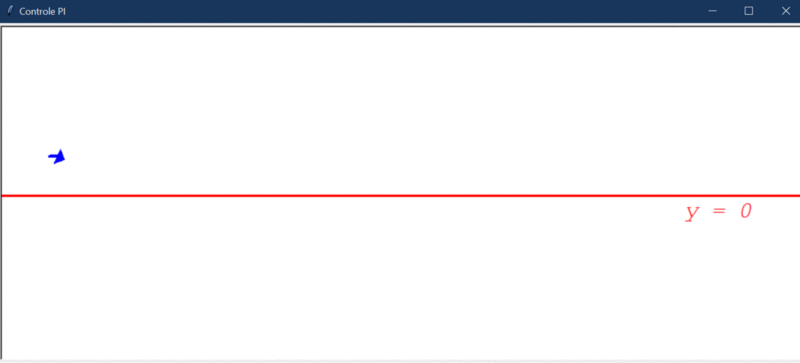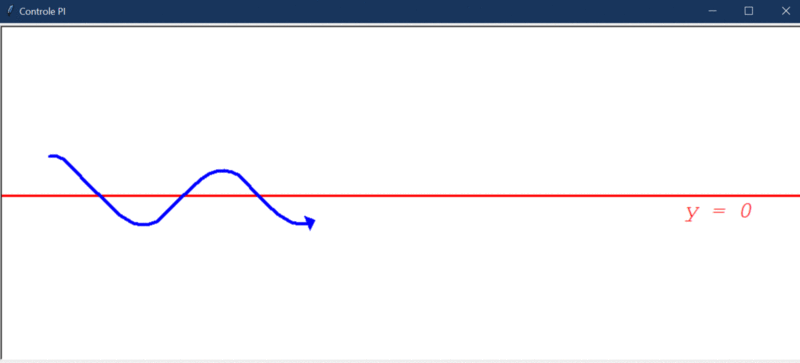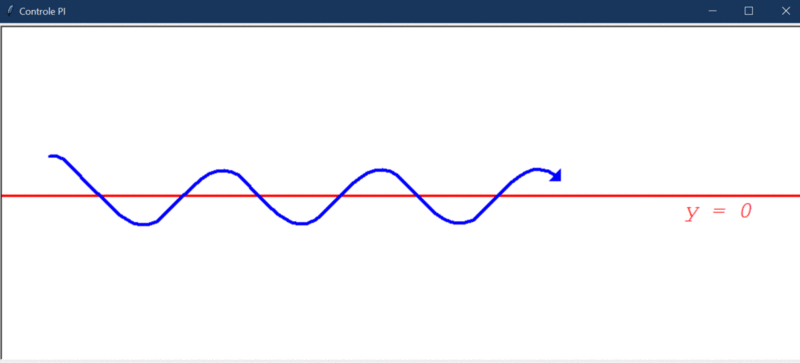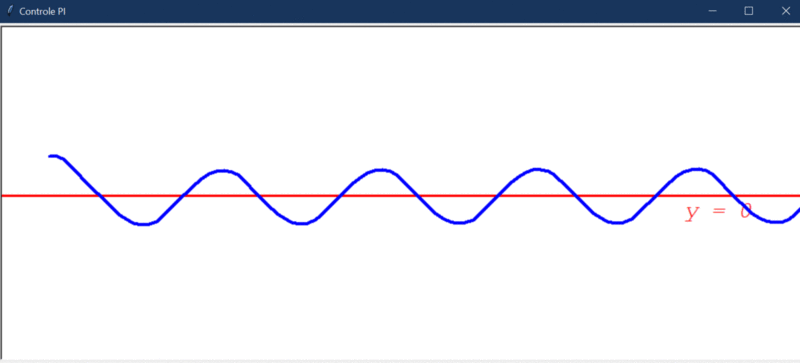
Controlador PI

Algumas observações cabíveis:

  • O controlador PI é capaz de direcionar o robô a um estado de menor erro, mas, por conta da instabilidade natural do sistema, ele não consegue levar e manter o erro em 0.

A princípio, não existe diferença aparente entre esse resultado e o resultado do controlador P sozinho, mas a diferença será percebida no próximo teste. Vejamos agora o resultado do teste com distúrbio:

Controlador PI com distúrbio

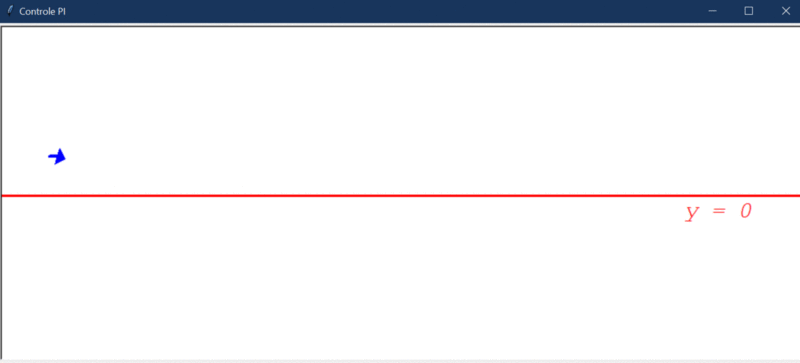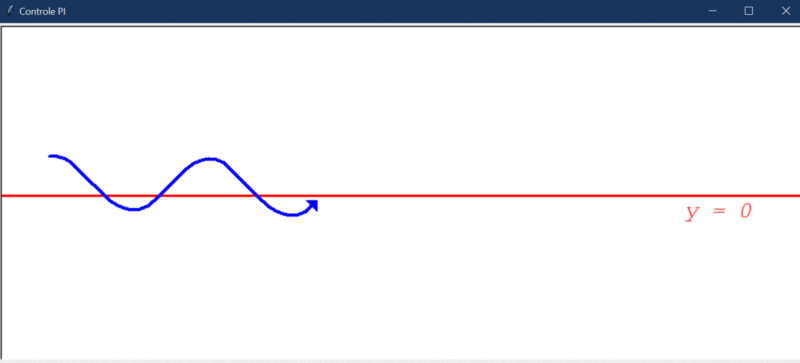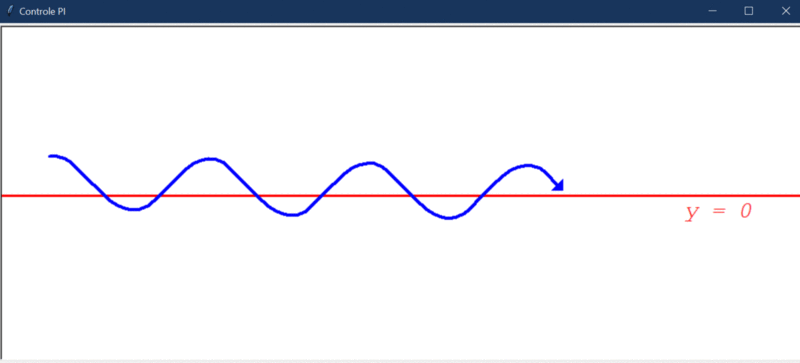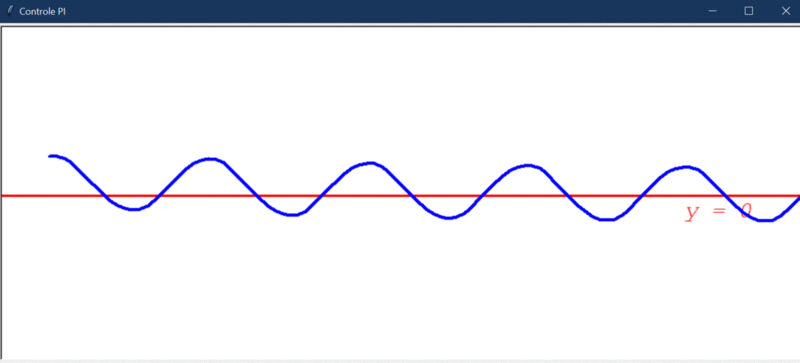
É possível perceber que o controlador aos poucos vai eliminando o “offset” que existe no erro e, após um tempo, o robô oscila ao redor de Y = 0. Esse fato fica mais evidente pelo gráfico da evolução do erro:

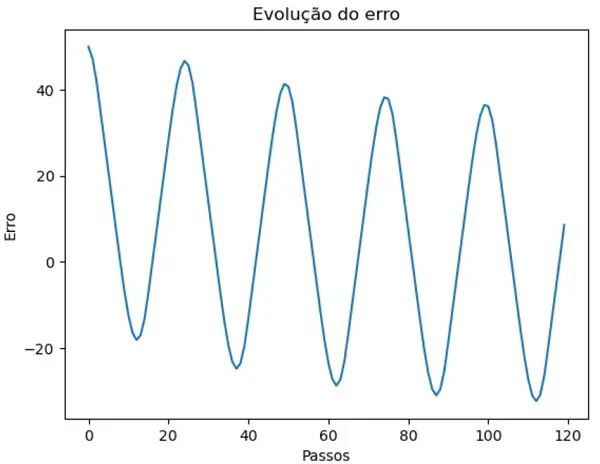
Evolução do erro do controlador PI com distúrbio

Controlador proporcional derivativo (ou controlador PD)

O controlador PD combina os controladores P e D em um só. Portanto, algumas vantagens e desvantagens são compartilhadas.

Fórmulas

Diante do mencionado acima, o controlador PD segue as seguintes fórmulas:

Inicializa com erro_anterior = 0

erro_diferenca = erro_atual – erro_anterior

controlador = erro_atual * GANHO_P + erro_diferenca * GANHO_D

Os parâmetros GANHO_P e GANHO_D são os mesmos de antes. Embora os valores acima estejam sendo somados, no código completo eles estão invertidos por conta do motivo de antes (erro positivo = girar o robô com ângulo negativo).

Código completo

Para testar o controlador, realizei 2 testes: 1 normal e outro adicionando um distúrbio de 10º no movimento do robô.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import auxiliar

# 1º teste - Sem disturbio
robo = auxiliar.Robo("Controle PD")
# 2º teste - Disturbio de 10º
#robo = auxiliar.Robo("Controle PD", disturbio = 10)

GANHO_P = 0.5
GANHO_D = 1.8
erro = 0

STEPS = 120
for i in range(STEPS):
    erro_diferenca = robo.getYPos() - erro
    erro = robo.getYPos()
   
    controle = - erro * GANHO_P \
               - erro_diferenca * GANHO_D

    robo.move(controle)

robo.plotError()
robo.end()

Características do controlador PD

Conforme dito anteriormente, este controlador combina característica do controle P e D:

  1. Atua efetivamente no regime transitório (por conta do P e D). Mas também atua no regime permanente do sistema (por conta do P).
  2. Não garante erro 0 no regime permanente.
  3. Pode melhorar a estabilidade do sistema (por conta do D).
  4. O aumento do GANHO_D pode gerar uma resposta inicial mais rápida, mas deixa o período de transição total mais lento.

Resultados

Após rodar o primeiro teste, este foi o resultado obtido:

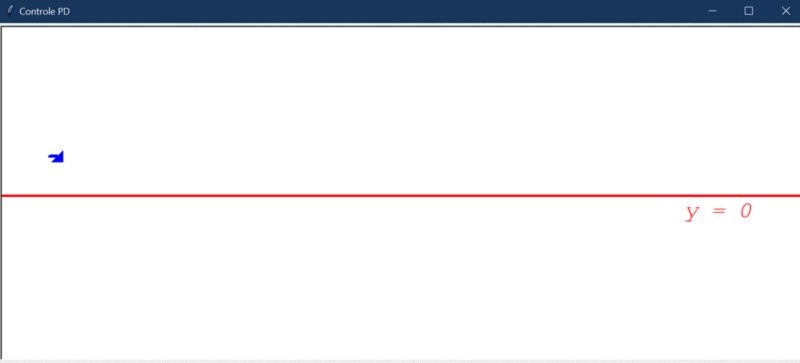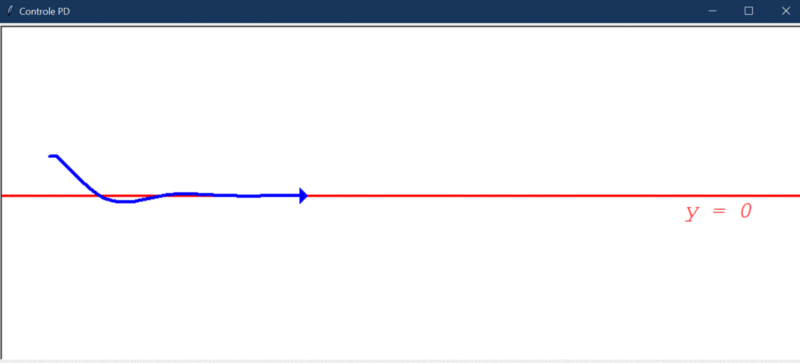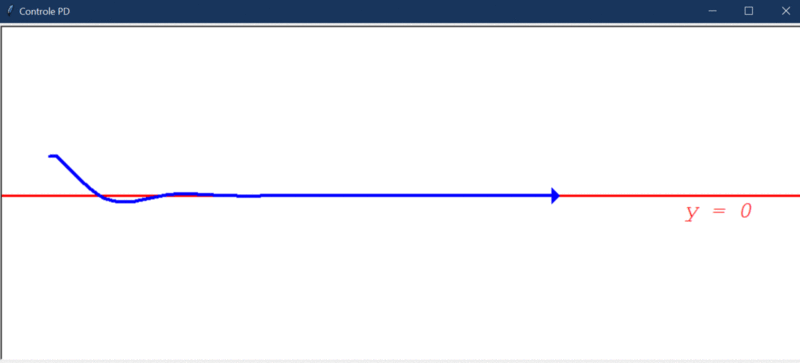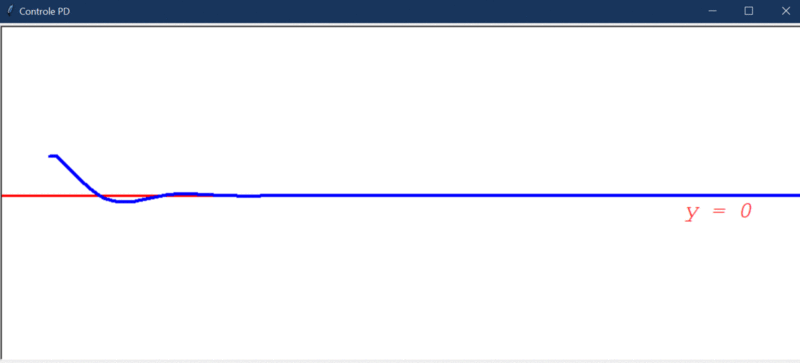
Controlador PD

Algumas observações cabíveis:

  • O controlador PD foi capaz de deixar o sistema estável.
  • Conseguiu direcionar o robô a um erro praticamente igual a 0 (cerca de -0,00000002).

Se o controlador D já estava bom, o PD é ainda melhor. Graças ao controlador P, podemos adicionar disturbios maiores sem provocar um aumento desenfreado do erro. Vejamos como ele se comporta com a adição do distúrbio (10º):

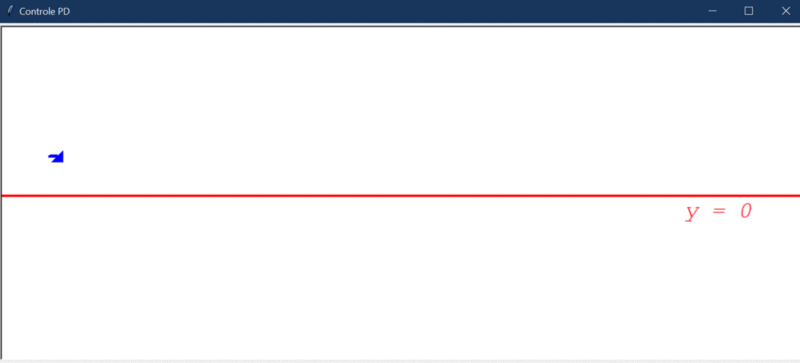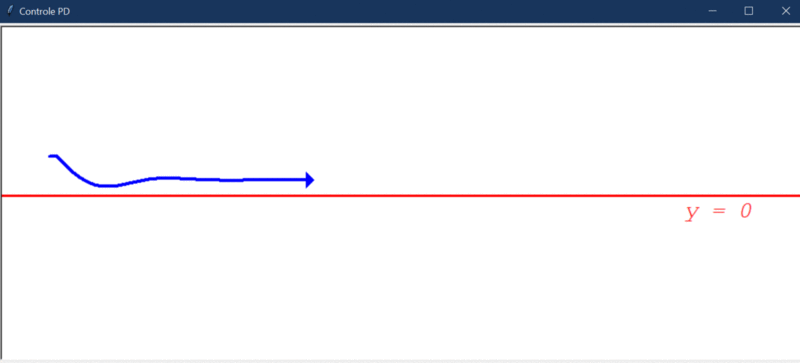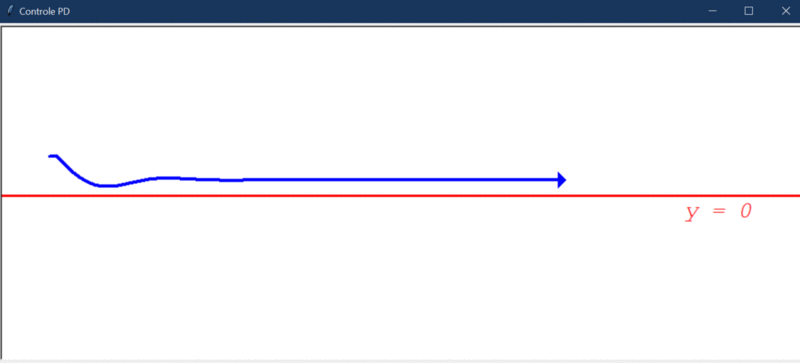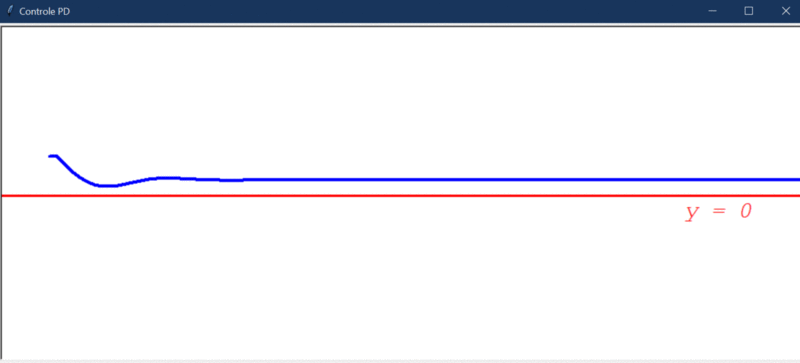
Controlador PD com distúrbio

Devido ao distúrbio, o erro final apresenta um “offset” e o controlador não é capaz de levá-lo a 0. Portanto, o controlador PD ainda não é bom o suficiente.

Controlador proporcional integral derivativo (ou controlador PID)

O controlador PID combina o melhor dos três mundos: P, I e D em um só. Algumas vantagens e desvantagens são compartilhadas.

Fórmulas

Diante do mencionado acima, o controlador PID segue as seguintes fórmulas:

Inicializa com erro_anterior = 0 e erro_acumulado = 0

erro_diferenca = erro_atual – erro_anterior

erro_acumulado = erro_acumulado + erro_atual

controlador = erro_atual * GANHO_P + erro_acumulado * GANHO_I + erro_diferenca * GANHO_D

Os parâmetros GANHO_P, GANHO_I e GANHO_D são os mesmos de antes. Embora os valores acima estejam sendo somados, no código completo eles estão invertidos por conta do motivo de antes (erro positivo = girar o robô com ângulo negativo).

Código completo

Para testar o controlador, realizei 2 testes: 1 normal e outro adicionando um distúrbio de 10º no movimento do robô.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import auxiliar

# 1º teste - Sem disturbio
robo = auxiliar.Robo("Controle PID")
# 2º teste - Disturbio de 10º
#robo = auxiliar.Robo("Controle PID", disturbio = 10)

GANHO_P = 0.5
GANHO_D = 1.8
GANHO_I = 0.01

erro = 0
erro_acumulado = 0

STEPS = 120
for i in range(STEPS):
    erro_diferenca = robo.getYPos() - erro
    erro = robo.getYPos()
    erro_acumulado += erro
   
    controle = - erro * GANHO_P \
               - erro_diferenca * GANHO_D\
               - erro_acumulado * GANHO_I

    robo.move(controle)

robo.plotError()
robo.end()

Características do controlador PID

Conforme dito anteriormente, este controlador combina característica do controle P, I e D:

  1. Atua efetivamente no regime transitório (por conta do P e D) e no regime permanente (por conta do I).
  2. Garante erro 0 no regime permanente (por conta do I).
  3. Pode melhorar a estabilidade do sistema (por conta do D).
  4. A resposta do sistema é mais lenta que no PD (por conta do I).
  5. O aumento do GANHO_D pode gerar uma resposta inicial mais rápida, mas deixa o período de transição total mais lento.
  6. Aumentar o GANHO_I pode deixar a resposta mais rápida, mas também mais oscilatória.

Resultados

Após rodar o primeiro teste, este foi o resultado obtido:

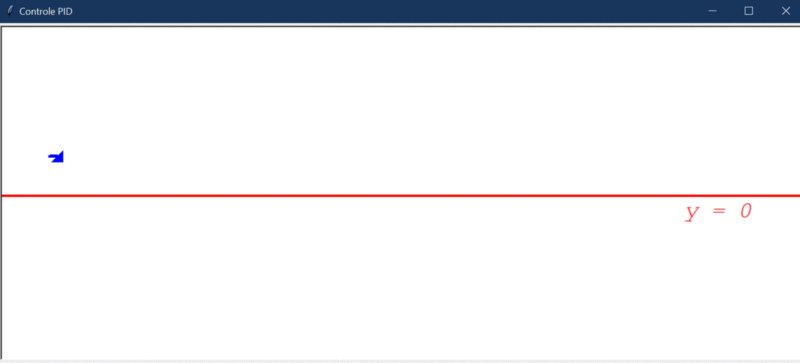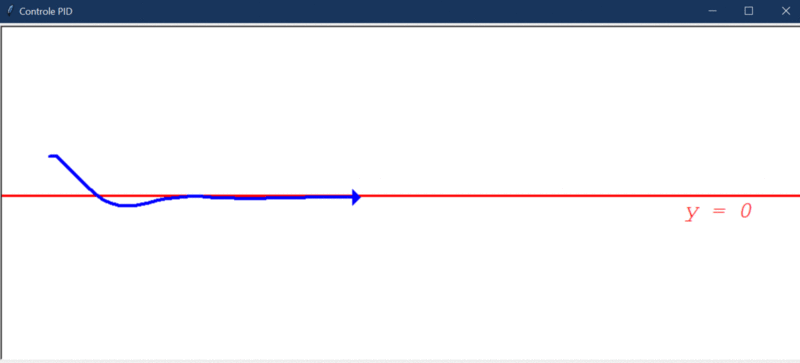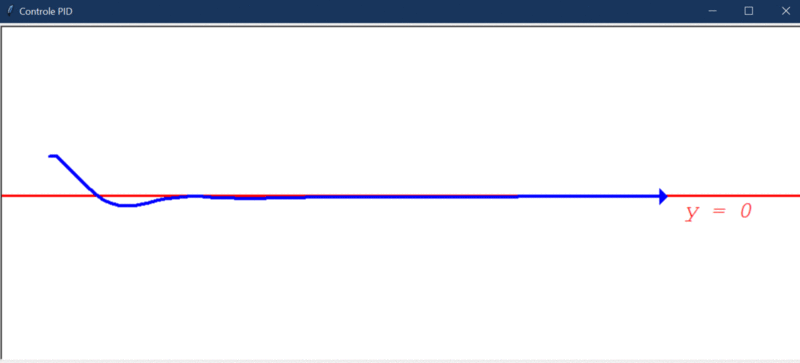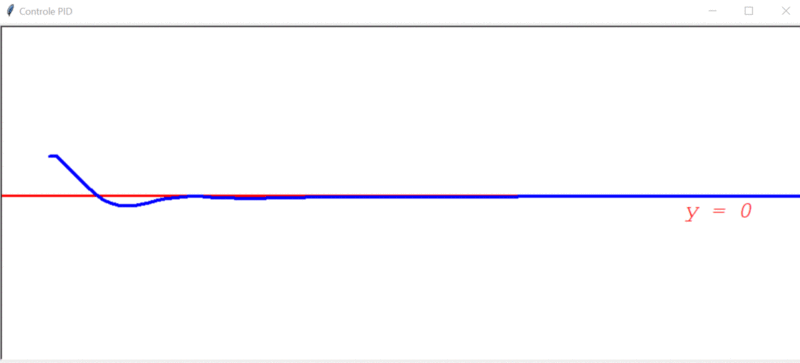
Controlador PID

Algumas observações cabíveis:

  • O controlador PID foi capaz de deixar o sistema estável.
  • Conseguiu direcionar o robô a um erro próximo de 0.

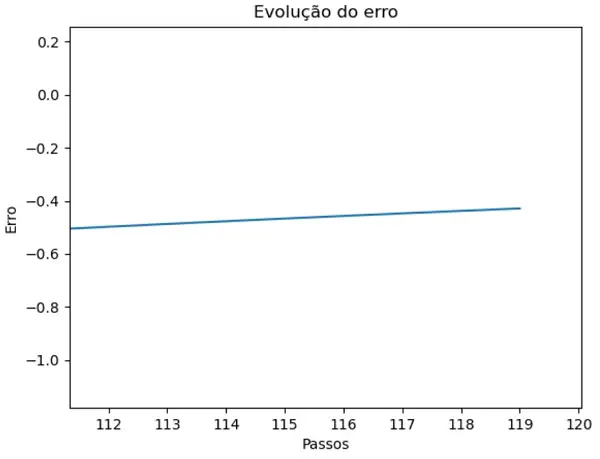
Por conta do controle I, o erro eventualmente chega a zero sim, mas ele demora mais comparado ao PD sem distúrbio. Veja o trecho final do gráfico da evolução do erro abaixo:

Erro do controlador PID em regime permanente

Pra bater o martelo e verificar se o PID é bom mesmo, vejamos como ele se comporta com a adição do distúrbio (10º):

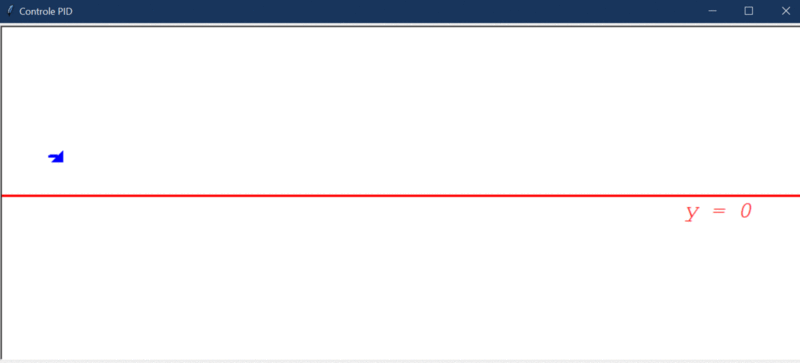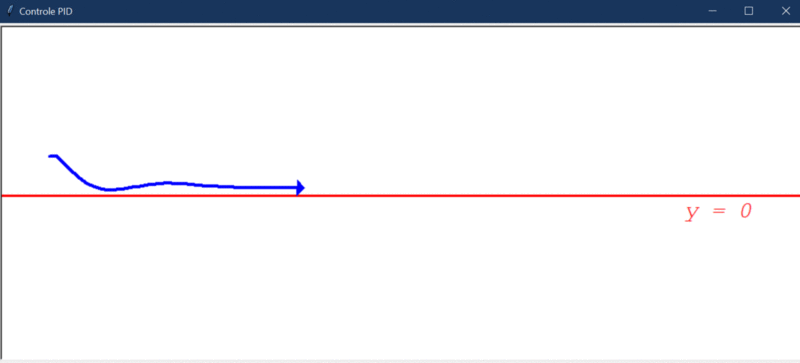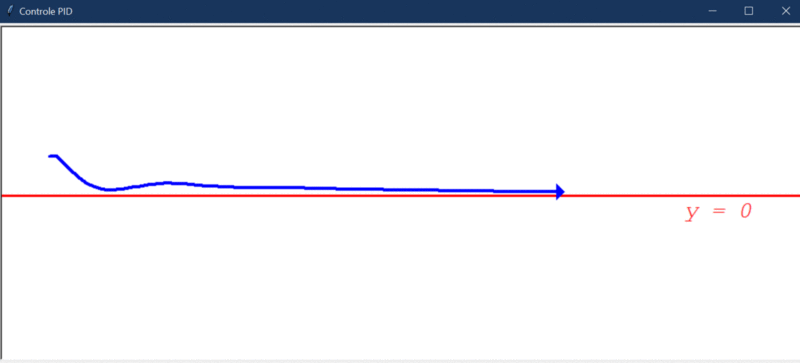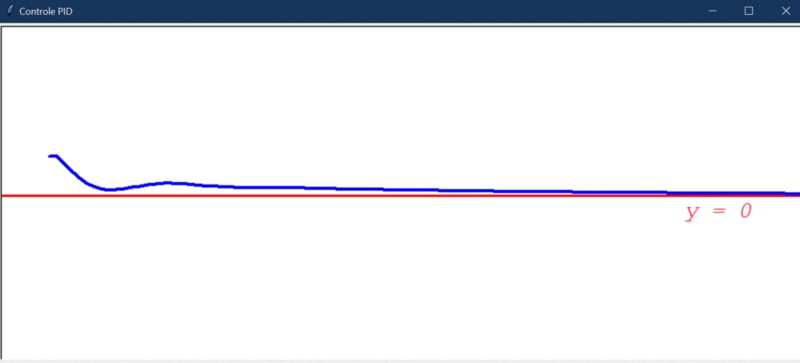
Controlador PD com distúrbio

Por fim, temos um controlador que é capaz de levar o erro a 0 mesmo com um distúrbio significativo. Isso, graças a combinação das características positivas dos controladores P, I e D. Entretanto, assim como mencionado no teste 1, a resposta é bem mais lenta e o erro demora a chegar em 0 de fato. Veja o trecho final do gráfico da evolução do erro:

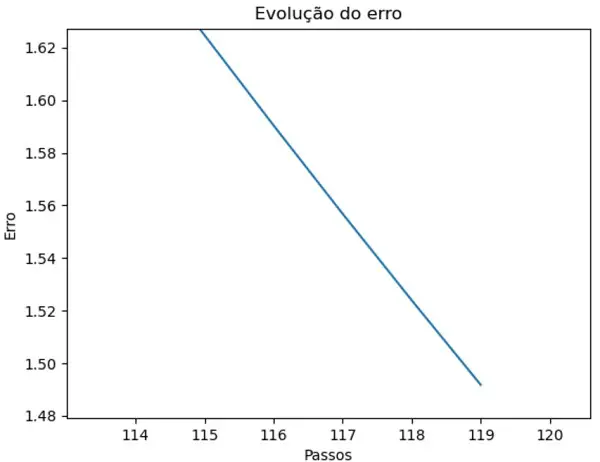
Erro do controlador PID com distúrbio

Observações finais

Recomendo bastante que você rode os códigos e experimente fazer alterações para fixar e entender melhor os assuntos abordados. 

A ideia deste post foi ensinar o controle PID para que ele possa ser utilizado para controlar robôs no mundo real. Além do PID, você também pode precisar implementar outras técnicas, como a de localização de um robô em um determinado ambiente.

Enfim, futuramente farei posts aplicando o PID para, por exemplo, controlar um robô pendulo invertido e um drone.