O circuito tanque tem aplicações bem interessantes nos circuitos de RF e apresenta funcionamento bem simples. Sendo assim, neste post, veremos o que é o circuito tanque, como ele funciona e algumas aplicações.
Recomendo ler o post sobre capacitores aqui do site, pois tem muita relação com o que será falado.
O que é o circuito tanque
O circuito tanque é, basicamente, um circuito composto por um indutor (L) e um capacitor (C) ligados em paralelo conforme imagem abaixo. Por conta disso, ele também é chamado de circuito LC.
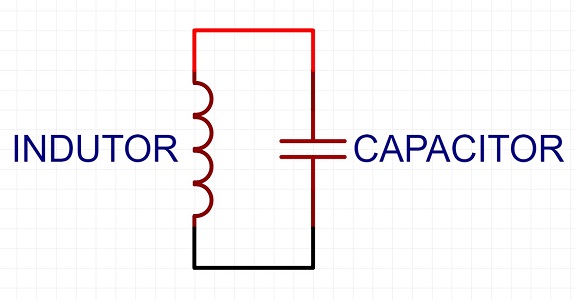
Assim como você pode ter imaginado, ele não é um circuito completo em termos de funcionar por conta própria. Sendo assim, ele é agregado em outros circuitos, por exemplo nos circuitos de rádio, para desempenhar a função de sintonizador. O significado de sintonia aqui é que o circuito tanque é capaz de “selecionar” um sinal de uma determinada frequência.
Para entender melhor, vamos pensar em um receptor de rádio: Ao mesmo tempo, sinais de diferentes frequências chegam na antena do rádio, pois existem diversas estações de rádio transmitindo seus programas simultaneamente. Então, para podermos ouvir apenas a rádio que gostamos, precisamos de um circuito capaz de “selecionar” o sinal que possui a frequência daquela rádio. E é aí que entra o circuito tanque. Seguindo o mesmo exemplo do rádio, ele também pode ser empregado na transmissão para “selecionar” a frequência de transmissão.
Coloquei selecionar entre aspas, pois selecionar dá ideia de que um sinal é extraído enquanto os outros são totalmente removidos. Na prática, a sintonia aumenta a amplitude do sinal de uma determinada frequência e abaixa a amplitude dos sinais das outras frequências. Ou seja, os sinais indesejados ainda exercem alguma interferência. Isso é bem perceptível no rádio quando a sintonia não é bem feita e conseguimos ouvir duas rádios ao mesmo tempo. Isso ficará mais claro quando analisarmos o circuito mais à frente.
Vou deixar para falar das aplicações do circuito tanque após a explicação do funcionamento, pois fará mais sentido, mas, por enquanto, entenda que ele serve para sintonizar sinais em termos de frequência.
Funcionamento do circuito tanque
Vou dividir a explicação em etapas, pois acho que facilitará o entendimento.
E acho importante mencionar que podemos entender o circuito de duas formas: analisando as impedâncias ou interpretando o circuito como um filtro. As duas analises, no fim das contas, são iguais, mas alguns entendem filtros de forma mais fácil do que a análise de impedâncias ou vice-versa. Esse tópico explicará o circuito seguindo a análise de impedâncias e o tópico seguinte explicará com a interpretação de filtro.
Circuito base
Para iniciar o entendimento, vejamos como o circuito tanque se comporta quando ligamos uma fonte de sinal alternado. A imagem abaixo mostra um circuito com uma fonte de sinal alternado de frequência f, um indutor com indutância L e um capacitor com capacitância C.
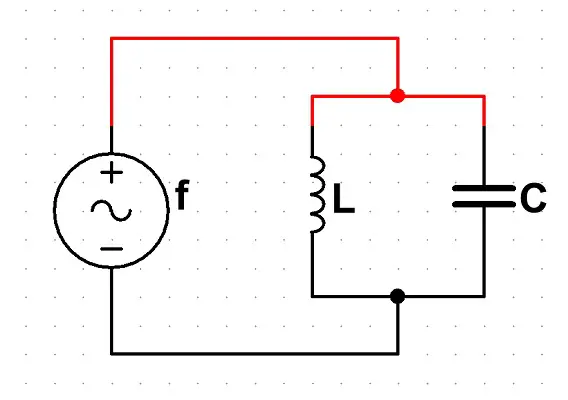
Pelo comportamento dos circuitos sob sinais alternados, sabemos que o indutor e o capacitor vão apresentar uma impedância, que, para cada caso é dada pelas expressões (módulo):
|Z_L| = 2 \times \pi \times f \times L
|Z_C| = \frac{1}{(2 \times \pi \times f \times C)}
Agora, vejamos o que obtemos quando plotamos um gráfico de ZL (para L = 10 μH) em função de f e outro de ZC (para C = 1 μF) em função de f. Não se preocupe com os valores de L e C, pois, por enquanto, estamos preocupados com os formatos das curvas que são semelhantes para qualquer L e C. Veja abaixo:
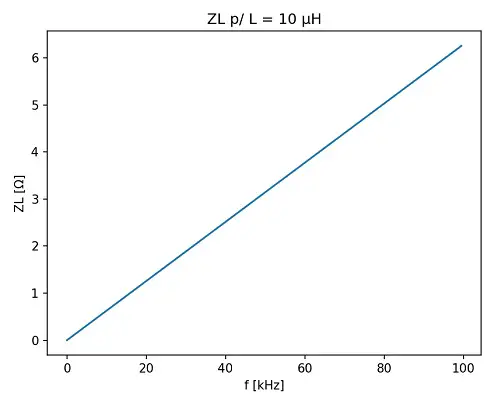
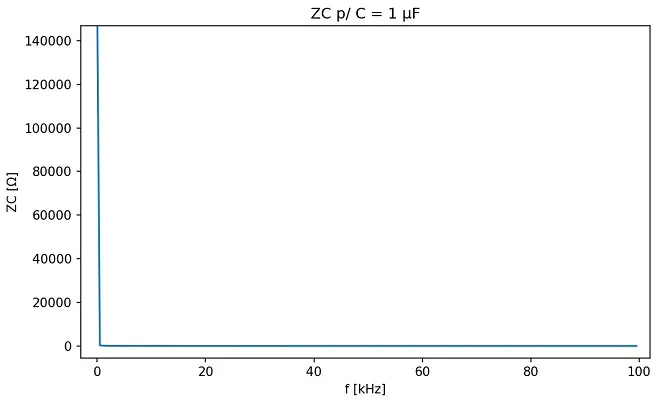
Até então nada de muito diferente do esperado: ZL começa em 0 e seu valor cresce à medida que a frequência aumenta; Zc começa tendendo ao infinito e seu valor diminui rapidamente à medida que a frequência aumenta (em 1 kHz, Zc já caiu de infinito para 159 Ω) . O interessante de se observar é que, enquanto ZL aumenta, Zc diminui. Essa característica é a chave do entendimento do circuito tanque.
Impedância equivalente
Agora, vamos plotar o gráfico da impedância equivalente (Zeq), que seria ZL e ZC em paralelo. Antes, vamos definir a expressão de Zeq. A expressão padrão de duas impedâncias em paralelo é:
Z_{EQ} = \frac{Z_L \times Z_C}{Z_L + Z_C}
É importante lembrar que as expressões de ZL e ZC que mostrei anteriormente são do módulo e, na equação acima, precisamos levar em conta a direção e sentido dos vetores ZL e ZC. É sabido que ambos estão na mesma direção (no eixo imaginário j) e sentidos contrários. No caso, ZL será +j e Zc -j. Então:
Z_{EQ} = \frac{j|Z_L| \times -j|Z_C|}{j|Z_L| – j|Z_C|} = \frac{|Z_L| \times |Z_C|}{j(|Z_L| – |Z_C|)}
Lembrete: j*-j = raiz(-1)*-raiz(-1) = -(-1) = 1.
Como estamos interessados no módulo, podemos considerar:
|Z_{EQ}| = \frac{|Z_L| \times |Z_C|}{||Z_L| – |Z_C||}
E o gráfico desta expressão é o seguinte:
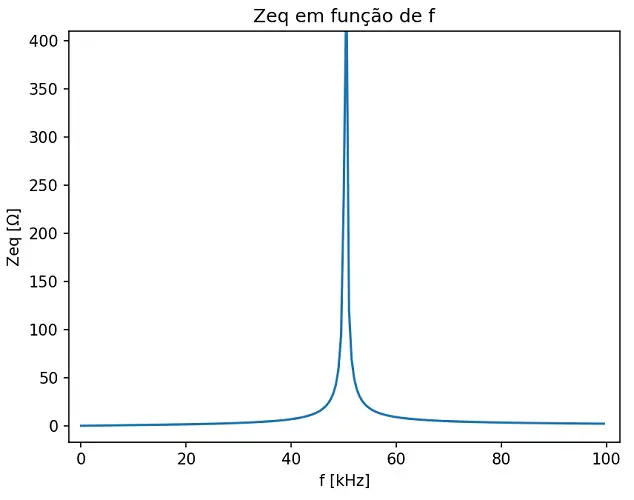
Em determinada frequência, a impedância equivalente tende ao infinito. Isso é esperado já que, no denominador da expressão de ZEQ, temos |ZL| – |ZC|. Ou seja, em uma certa frequência, o valor de ZL e ZC serão iguais, a subtração será zero e isso fará o resultado tender ao infinito. Essa frequência onde isso ocorre é chamada de frequência de ressonância.
Frequência de ressonância
Conforme vimos acima, a frequência de ressonância é a frequência que faz |ZL| ser igual à |ZC|. Por conta disso, podemos definir uma expressão para calcular essa frequência:
|Z_L| = |Z_C|
2 \times \pi \times f \times L = \frac{1}{(2 \times \pi \times f \times C)}
Manipulando a equação, chegamos ao seguinte:
f^2 = \frac{1}{(4 \times \pi^2 \times L \times C)}
f = \sqrt{\frac{1}{(4 \times \pi^2 \times L \times C)}}
f_{ressonância} = \frac{1}{2 \times \pi \times \sqrt{L \times C)}}
Para ter certeza, vamos calcular a frequência de ressonância do circuito do tópico anterior (C = 1 μF e L = 10 μH).
f_{ressonância} = \frac{1}{2 \times \pi \times \sqrt{10\mu \times 1\mu)}} = 50,33 kHz
Olhando o gráfico do tópico anterior, podemos dizer que o cálculo faz todo sentido.
Impedância na frequência de ressonância
Agora que entendemos sobre a frequência de ressonância, qual é a relação disso com a sintonia que foi falada no começo do post? Para responder essa pergunta, vamos combinar o circuito tanque com uma resistência:
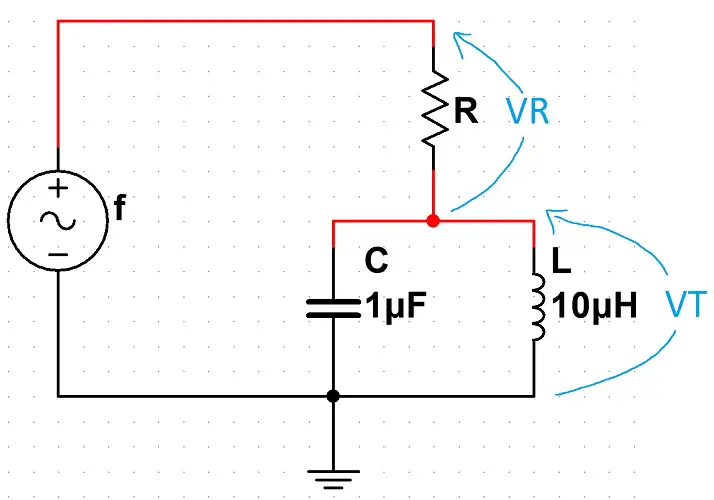
Nessa configuração, podemos interpretar o circuito como um divisor de tensão. E, a fórmula do divisor de tensão é dada pela expressão abaixo (é a igual à equação padrão de divisor de tensão, mas com impedâncias):
V_T = \frac{Zeq*Vs}{Z_R + Zeq}
Onde Vs é a tensão da fonte, ZR é a impedância de R e Zeq é a impedância equivalente do circuito tanque.
Como vimos no gráfico de impedância equivalente, o valor dela é pequeno (tende a zero) para frequências diferentes da frequência de ressonância. Nesses casos, teríamos:
V_T = \frac{0*Vs}{Z_R + 0} \cong = 0
Ou seja, longe da frequência de ressonância, a tensão VT é próxima de zero. Agora, vamos analisar para o caso de um sinal com frequência igual à da de ressonância. Nesse cenário, Zeq tende a infinito:
V_T = \frac{\infty *Vs}{Z_R + \infty} \cong \frac{\infty}{\infty} \times V_S \cong V_S
Portanto, na frequência de ressonância, VT tende a ter a mesma amplitude que Vs. Ao simular o circuito e gerar a resposta em frequência dele, podemos ver como é o comportamento da tensão:
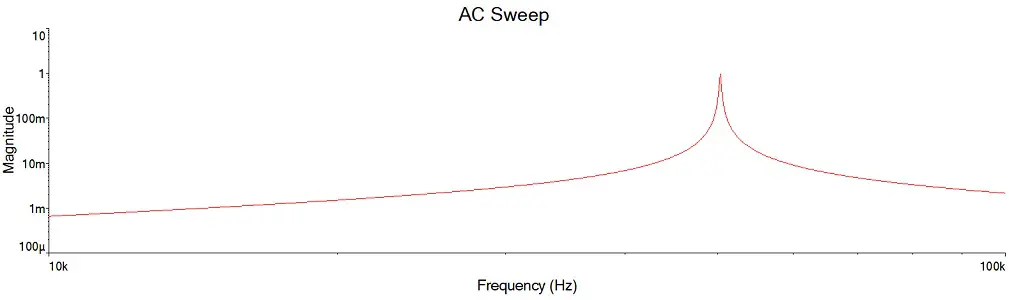
No gráfico acima, Vs = 1, por isso o valor máximo de VT é 1. Uma observação interessante de ser feita é que, em boa parte do espectro de frequências, a amplitude fica abaixo de 10m, isto é, abaixo de 0,01 Vs.
Exemplo prático de funcionamento
Seguindo o raciocínio do tópico anterior, vamos analisar um circuito real onde o circuito tanque é aplicado. No caso, é o circuito do rádio galena. Caso tenha interesse em entender melhor, leia o post sobre o assunto. A ideia aqui é focar no funcionamento do circuito tanque. Veja o circuito abaixo:
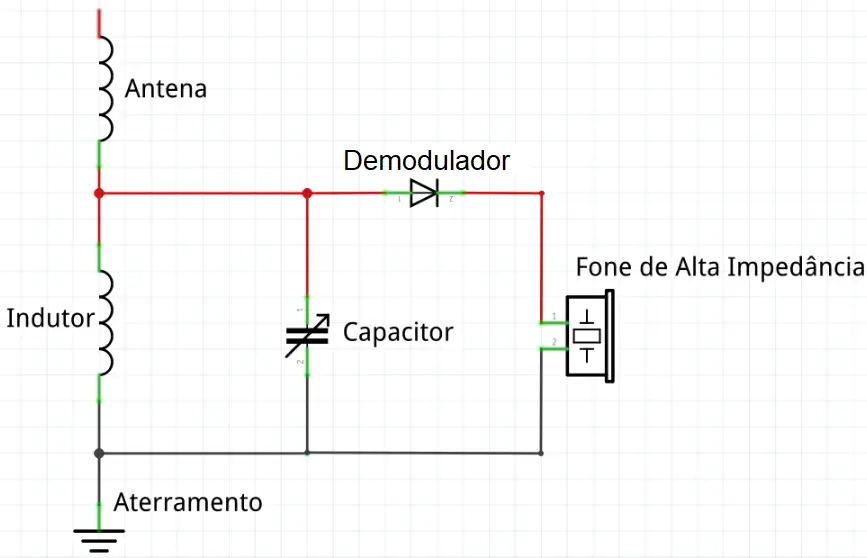
Repare que o sinal recebido na antena vai direto para um circuito tanque e, logo depois, o sinal sintonizado vai para um demodulador (diodo). Tendo em vista as explicações anteriores, fica tranquilo entender que os sinais da frequência sintonizada terão maior amplitude do que os sinais com frequência muito diferente da de ressonância. Ou seja, o circuito LC basicamente atenua os sinais de frequência diferente da desejada e deixa o sinal desejado em evidência.
Agora, imagine que uma rádio AM transmite na frequência de 800 kHz e outra na frequência de 810kHz, se você sintonizar o rádio galena na frequência de 805 kHz (no meio das duas rádios), é possível que a amplitude do sinal das duas rádios seja a mesma e você ouvirá as duas rádios ao mesmo tempo na mesma intensidade. É por isso que expliquei a sintonia como sendo uma “seleção” com aspas, já que ela não elimina os sinais e sim atenua.
Outras interpretações
Pensando no circuito como um filtro
Ao invés da análise mais demorada das impedâncias, podemos pensar no circuito LC como sendo um filtro. Recapitulando o circuito:

O capacitor tende a se comportar como um circuito aberto em baixas frequências (tensão contínua) e como curto em altas frequências (f = infinito). Por outro lado, o indutor tende a se comportar como um curto em baixas frequências (tensão contínua) e como circuito aberto em altas frequência (f = infinito). Combinando os dois, temos um circuito que se comporta como curto em frequências baixas (tensão contínua) e altas frequências (f = infinito) e, no meio termo, que seria a frequência de ressonância, ele vai apresentar uma condição semelhante a um circuito aberto (impedância infinita).
Esse tipo de filtro criado pelo circuito da imagem anterior é conhecido como filtro passa-faixa. E, o diagrama de bode do circuito da imagem anterior é o seguinte (a resposta em frequência eu já tinha mostrado no tópico “Impedância na frequência de ressonância”):
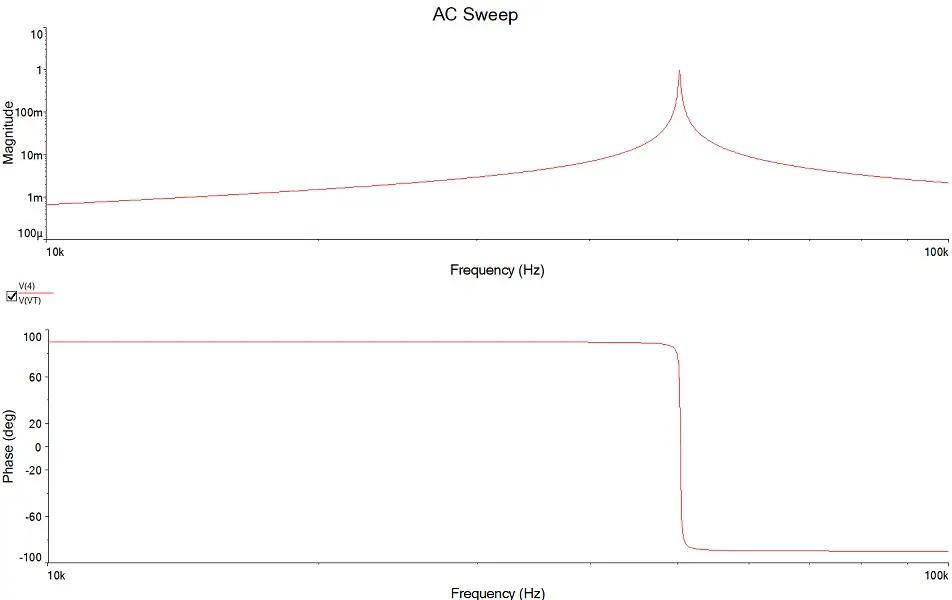
Repare que antes da frequência de ressonância, o circuito tem comportamento indutivo, pois o ângulo de fase é positivo (corrente defasada em 90º), mas, após a frequência de ressonância, ele passa a ter comportamento capacitivo apresentando ângulo de fase negativo (corrente adiantada em 90º). Isso ocorre por causa das curvas de impedância que mostrei anteriormente (ZL cresce à medida que ZC diminui).
Se invertermos a posição do resistor com o capacitor + indutor, o circuito vira um filtro rejeita-faixa e o diagrama de bode dele passa a ser o seguinte:
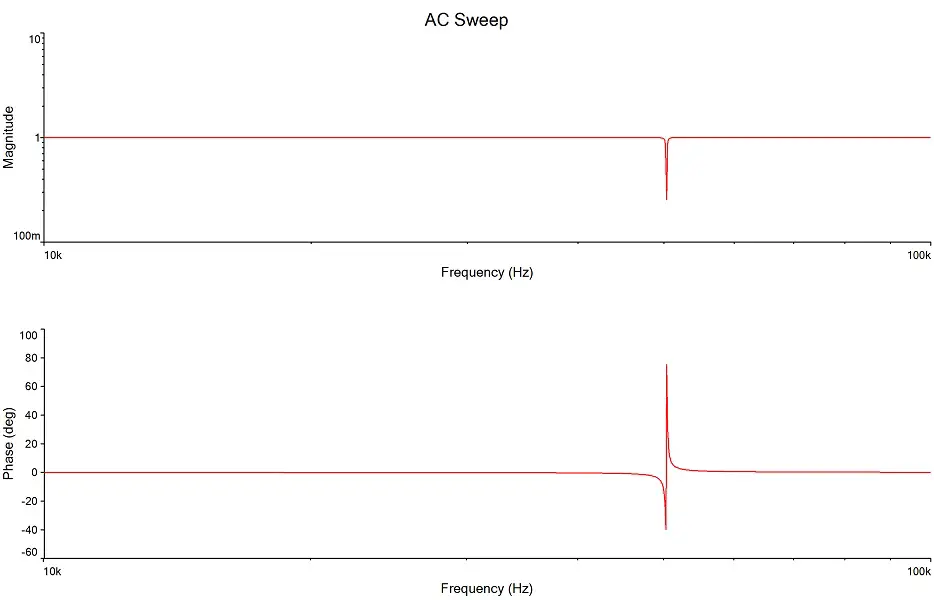
Nesse caso, o ângulo de fase é 0º para quase toda a faixa, pois o sinal analisado é em cima da resistência, a qual não atrasa e nem adianta a corrente.
Pensando na carga e descarga do capacitor e indutor
Há ainda uma terceira forma de visualizar o circuito tanque, que é por meio da carga e descarga do capacitor no indutor e vice-versa. Para isso, vamos retornar ao primeiro circuito do post:

Se considerarmos o capacitor inicialmente carregado e o indutor descarregado, o seguinte acontecerá: o capacitor descarregará no indutor e o indutor será carregado aos poucos. À medida que isso ocorre, a tensão em cima do circuito (VT) tende a 0.
Quando o capacitor termina de descarregar, o ciclo se inverte e o indutor começa a descarregar no capacitor. Esse processo é ilustrado no gif abaixo:

A tensão fica se invertendo nesse processo e ela apresenta caráter oscilatório. É por isso que o circuito tanque também é conhecido como circuito ressonante (fica vibrando/oscilando de um lado pro outro em uma determinada frequência). A oscilação não é permanente, já que o circuito na prática possui elementos que dissipam a energia (resistências parasitas). Então, a oscilação começa com amplitude máxima e vai caindo aos poucos.
A grande questão é que essa frequência de oscilação do circuito é justamente a frequência de ressonância que foi discutida nos outros tópicos. Para provar isso, veja o resultado da simulação, onde medi a tensão no circuito tanque com C = 1 μF e L = 10 μH:
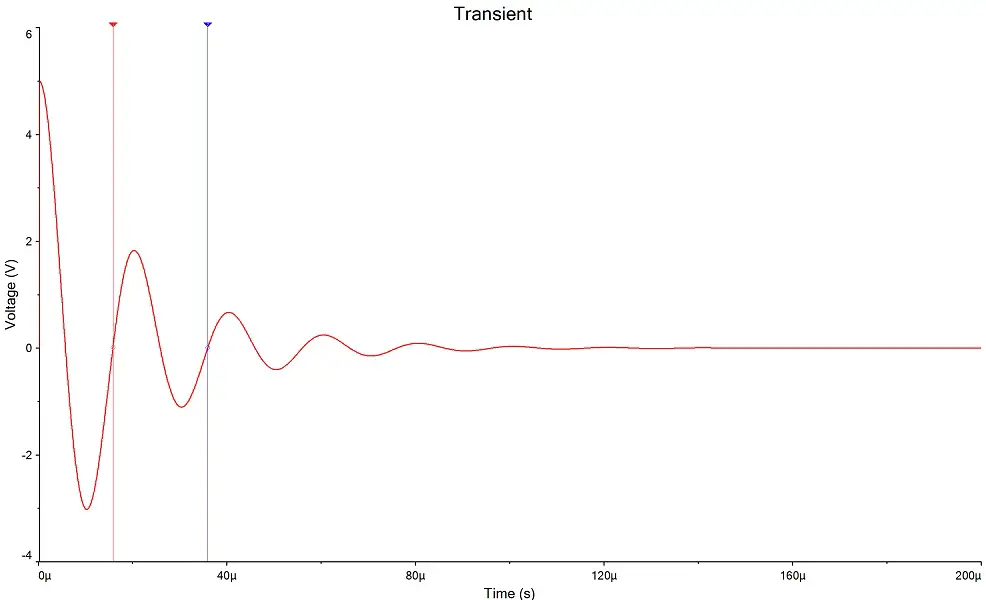
Os cursores estão aproximadamente entre 1 ciclo de oscilação e o tempo entre eles é de 20,13 μs. Em termos de frequência, isso dá cerca de 49,7 kHz, que é um valor bem próximo da frequência de ressonância calculada no tópico “Frequência de ressonância”. A diferença desse valor pro valor calculado anteriormente provavelmente é causada por uma imprecisão na medição que fiz.
Aplicações do circuito tanque
Agora que entendemos o funcionamento do circuito tanque, vejamos algumas aplicações:
- Rádio galena:
- O circuito tanque tem papel de “selecionar” qual rádio será demodulada e ouvida no alto falante.
- Oscilador Colpitts:
- Transmissor de sinal de RF que utiliza um circuito tanque para sintonizar a frequência de transmissão. Além disso, usa um divisor de tensão capacitivo na realimentação.
- Oscilador Hartley:
- Transmissor de sinal de RF que utiliza um circuito tanque para sintonizar a frequência de transmissão. Além disso, usa um divisor de tensão indutivo na realimentação.
Observações finais
O post mostrou o circuito LC paralelo, mas preciso salientar que o circuito LC série também apresenta comportamento similar, mas com lógica trocada: na frequência de ressonância (|ZL| = |ZC|) a impedância equivalente é 0 (e não infinita), pois:
Z_{EQ} = +j|ZL| – j|ZC| = 0
Ou seja, na configuração resistor + LC série, ele será um filtro rejeita-faixa e, na configuração LC série + resistor, ele será um filtro passa-faixa.
Rádio Galena
