Os circuitos digitais sequenciais possibilitam a criação de sistemas complexos, que são a base dos circuitos encontrados nos mais diversos dispositivos. Sendo assim, nesta aula, aprenderemos sobre o primeiro elemento do circuito sequencial, o Latch.
Na aula anterior, aprendemos sobre os multiplexadores e demultiplexadores, elementos bem importantes na telecomunicação.
Informações básicas
O que é o circuito sequencial
Na aula 6, estudamos sobre o circuito combinacional, que é um circuito em que o estado de sua saída depende apenas do estado atual de sua entrada. No caso do circuito sequencial, o estado de sua saída depende do estado atual da entrada e dos estados passados dela.
Ou seja, dependendo de como o circuito foi acionado anteriormente, a saída atual pode reagir de forma diferente. Por exemplo, imagine que você deseja projetar um circuito de uma campainha a qual só deve tocar se a pessoa está apertando pela primeira vez. Veja o desenho do sistema da campainha abaixo:
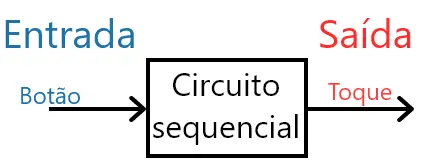
Neste caso, a saída só será 1 se o botão for 1 pela primeira vez. Ou seja, inicialmente S = 1 se E = 1 (S = E). Mas, se o botão já foi apertado, S = 0 mesmo que E = 1. Então, a condição S = E não é mais válida, pois S depende também do estado anterior de E.
Isso ficará menos abstrato no tópico seguinte.
Memória
Agora, você pode estar se perguntando como o circuito é capaz de conhecer o estado anterior de E (entrada do exemplo anterior), já que isto parece uma tarefa complicada para as portas lógicas elementares apresentadas até então.
Bem, isto é alcançado por meio da capacidade de memória que os circuitos sequenciais tem. Isto é, eles conseguem memorizar valores (binários obviamente) de forma a armazenar estados anteriores do sistema.
Voltando ao exemplo da campainha, o sistema teria que ser capaz de memorizar a condição de que a campainha já foi tocada pela primeira vez. Sendo assim, a saída, dependeria do valor atual do botão e do valor armazenado na memória. Sendo mais específico, S = E.(¬M), sendo M o bit da memória que diz se a campainha já foi tocada ou não.
Mesmo assim, isso ainda não responde como portas lógicas elementares são capazes de memorizar valores. Adianto que isto é possível e pode ser feito de algumas formas diferentes. A primeira forma que veremos recebe o nome de Latch, que é um elemento capaz de memorizar um valor de 1 bit.
Latch
Ressalva
Adiante, introduziremos um circuito do Latch. Pode parecer que o circuito caiu de paraquedas e que não houve uma lógica clara até se chegar a ele. Bem, acontece que o Latch é um circuito um tanto quanto não intuitivo e, em algum momento, alguém chegou até ele e compartilhou sua descoberta. Portanto, a ideia aqui é apenas mostrar o circuito diretamente e explicá-lo.
E eu disse ‘um’ circuito, porque o Latch pode ser feito de algumas formas diferentes.
Introdução
Considere o seguinte circuito:
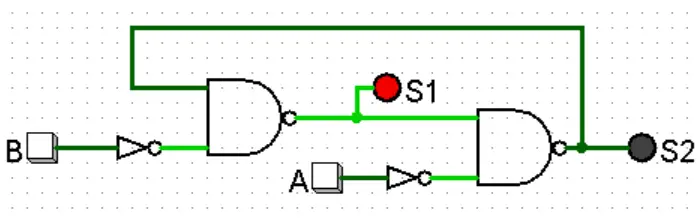
A principio, parece um circuito um pouco confuso, mas, se simplificarmos, fica mais fácil de entender. E, a partir das aulas anteriores, você já é capaz de fazer isto sem problemas. Então, vamos começar por S1:
S1 = ¬(S2.(¬B))
S2 = ¬((¬A).S1)
Agora, podemos substituir o valor de S1 na expressão de S2:
S2 = ¬((¬A).¬(S2.(¬B)))
Neste ponto, podemos aplicar o teorema de De Morgan para simplificar ainda mais:
S2 = ¬(¬A) + ¬(¬(S2.(¬B)))
S2 = A + S2.(¬B)
Com isto, a expressão final de S2 fica mais tranquila de entender. Repare que o valor de S2 depende também do valor de S2. Isto pode parecer paradoxal, mas é justamente esta dependência que cria a capacidade de memória do circuito. Para entender isto, você pode interpretar o S2 da direita como o estado passado de S2:
S2atual = A + S2passado . (¬B)
Funcionamento
Certo, agora vejamos algumas conclusões que podemos extrair da expressão simplificada mostrada acima:
- S2 sempre será 1 quando A for 1.
- Isto porque, fica S2 = 1 + S2.(¬B) = 1 (álgebra booleana).
- S2 será 0 se B = 1 e A = 0.
- S2 = A + S2 . (¬1) = A + S2 . 0 = A = 0
- Repare que S2 só é igual a 0, porque A = 0
- Se A=0 e B=0, o valor de S2 dependerá de seu estado passado.
- S2atual = 0 + S2passado.(¬0) = S2passado.1 = S2passado
Diante de todas estas condições, podemos analisar também a expressão de S1:
- A = 1 e B = 0 → S2 = 1 → S1 = 0
- A = 0 e B = 1 → S2 = 0 → S1 = 1
- A = 0 e B = 0 → S2 = S2passado → S1 = ¬S2passado
- A = 1 e B = 1 → S2 = 1 → S1 = 1
Em todas as situações anteriores (com exceção da última), o valor de S1 foi o contrário de S2. Então, no estudo dos Latches, considera-se que S1 = ¬S2 e o estado A = 1 e B =1 é chamado de estado proibido por quebrar esta regra.
Nomenclatura e simbologia
Nos tópicos anteriores, nomeei as entradas e saídas de forma a seguir o padrão que eu estava utilizando nas aulas anteriores. Mas, a correta nomenclatura para eles é diferente. Para explicar o formato padrão do Latch e seu símbolo, considere que aquele circuito anterior foi transformado em uma caixa de acordo com a seguinte imagem:
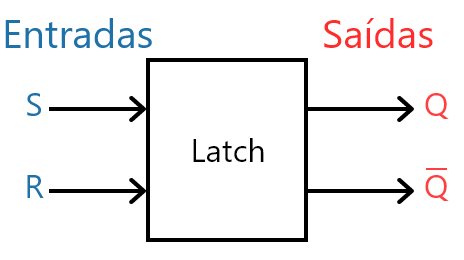
O Latch pode ser representado de acordo com a imagem acima e as siglas tem o seguinte significado:
- S ou Set: entrada responsável por ‘setar’ a saída. Isto é, colocá-la em 1.
- No exemplo anterior era a entrada A.
- R ou Reset: entrada responsável por ‘resetar’ a saída. Isto é, colocá-la em 0.
- No exemplo anterior era a entrada B.
- Q: saída do Latch.
- No exemplo anterior era a saída S2.
- ¬Q: saída invertida do Latch.
- No exemplo anterior era a saída S1.
Diferentes formas de criar o Latch
Em seguida, veremos alguns tipos diferentes de Latch e suas respectivas tabelas-verdade. E existem dois tipos principais de Latches, o Latch SR e o Latch D. A diferença será explicada nos tópicos abaixo.
Latch SR
O Latch SR é o mesmo apresentado até então.
Latch SR com portas NAND
Este é o mesmo circuito visto na explicação do tópico sobre o Latch, mas aqui mostrarei a forma mais comum de representá-lo:
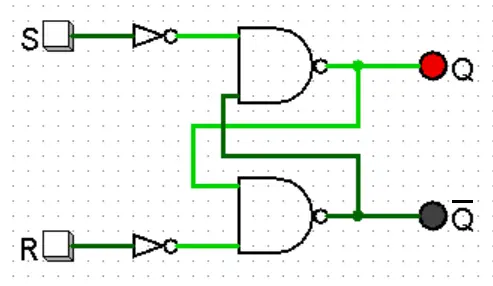
E, sua tabela-verdade:
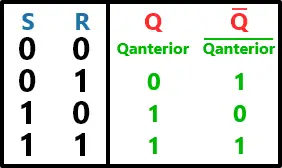
Latch SR com portas NOR
Circuito:
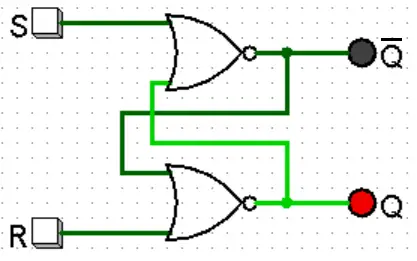
Tabela-verdade:
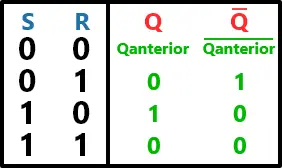
Latch com Enable
É possível adicionar uma entrada extra no Latch, que recebe o nome de Enable, para criar uma forma de habilitar/desabilitar as entradas em um momento desejado. Esta funcionalidade de definir a entrada no momento “certo” possibilita um sincronismo de todo o circuito. Neste ponto, surge um outro termo chamado “Clock”, mas esta questão será abordada na próxima aula.
Obs: O Enable é aplicável a todos os circuitos abordados, incluindo o que será mostrado no próximo tópico. Mas, decidi escolher o Latch SR com porta NOR para exemplificar.
Veja o circuito abaixo onde uma nova entrada (E) foi adicionada, que é o Enable.
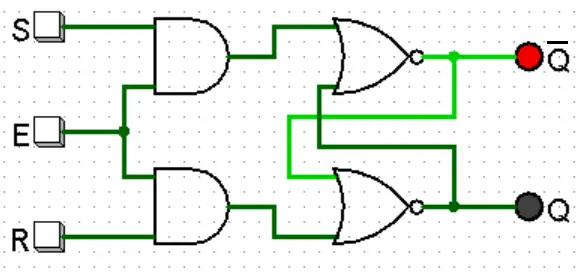
Repare que a única mudança para o circuito de antes foi adicionar duas portas AND antes de conectar S e R nas portas NOR. Portanto, conhecendo o comportamento da porta AND, fica evidente que as entradas S e R só terão algum efeito significativo se a entrada E for igual a 1.
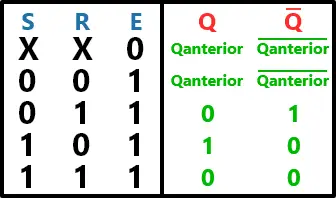
Ou seja, o Enable serve, de fato, para habitar ou desabilitar as entradas. E repare que, se E = 0, então as duas entradas que chegam às portas NOR também serão 0. E, nesta condição, Qatual = Qanterior. Isto é, o Enable não atua na saída, pois ela apenas se mantém. Isto está sintetizado na tabela-verdade abaixo:
Latch D
O Latch D junta as entradas SR em uma única chamada de D. O objetivo disto é de controlar o circuito utilizando apenas um entrada. Veremos como isto ocorre no tópico seguinte.
Latch D genérico
O circuito genérico está apresentado abaixo.
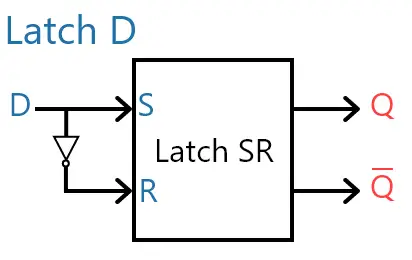
O Latch D pode ser criado apenas juntando as entradas e ligando uma delas em uma porta NOT. Com isto, S = D, R = ¬D, logo R = ¬S. Desta forma, seu funcionamento será o seguinte: Se D = 1, Q = 1 e, se D = 0, Q = 0. Logo, Q = D.
Este tipo de configuração faz com que o estado proibido (S = R = 1) não seja realizável. Veja a tabela-verdade abaixo:
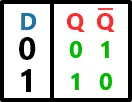
Olhando a tabela-verdade, dá a impressão que este é um circuito sem sentido. Mas ele é de fato útil quando utilizado com o Enable, pois aí utilizando apenas 2 duas entradas, você tem o mesmo funcionamento do Latch SR, além do sincronismo.
Latch D com Enable
Pretendo apenas comentar da existência deste tipo de circuito, pois ele é fácil de entender depois de termos visto os circuitos anteriores.
Bem, é possível adicionar a entrada de Enable ao Latch D para proporcionar uma forma de sincronismo ao circuito. Com isto, se E = 0, é possível fazer com que a saída seja igual ao valor passado, mesmo que a entrada D varie de valor.
Observações finais
Conforme pôde ser visto, os Latches trazem uma funcionalidade para os circuitos digitais que parece quase mágica. E essa capacidade de memória permite um armazenamento de dados utilizando circuitos digitais, como é o caso de um dos tipos de memória RAM. Mas lembrando que este é um tipo de memória volátil, a qual não retem os dados se o circuito for desenergizado.
Além disto, os Latches também permitem que criemos circuitos digitais ainda mais complexos. E veremos em uma aula futura como projetar um circuito sequencial de forma adequada, mas, antes, veremos sobre os Flip Flops, que são elementos bem parecidos com os Latches.
