O circuito combinacional é relativamente simples e permite a criação de diversos sistemas digitais. Sendo assim, nesta aula, aprenderemos a projetar um circuito combinacional entendendo suas etapas.
Na aula anterior, aprendemos sobre as expressões booleanas e como simplificá-las.
Informações básicas
O que é um circuito combinacional
Um circuito combinacional é um circuito digital que possui uma ou mais saídas que dependem apenas do estado ATUAL da(s) entrada(s).
Isto é, as entradas do circuito produzem um resultado “instantâneo” na saída. Só não é instantâneo por conta do atraso das portas lógicas, como foi discutido na aula 4.2.
Na aula anterior, os circuitos que foram mostrados eram circuitos combinacionais. Veja um deles na imagem abaixo:
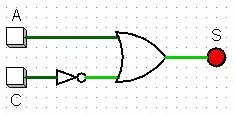
Observe que a saída S depende apenas do estado atual da saída A e da saída C. Sendo mais específico, S será 1 apenas se A for 1 e C for 0. Para qualquer outra combinação destas entradas, a saída S é 0. E o estado atual de A ou C não afeta o estado futuro da saída.
Se você lembrar bem, o circuito acima foi resultado de uma simplificação de uma expressão que também continha uma entrada B. Entretanto, a entrada B não apareceu no circuito final.
Isto quer dizer que B é desnecessário para o circuito final. Portanto, apesar da entrada B existir no contexto do circuito, ela pode ser ignorada e inutilizada. No tópico abaixo estas coisas farão mais sentido.
Significado real das entradas
Até agora nós tratamos as entradas de um circuito apenas como elementos que podem ter dois estados (0 ou 1). Mas o que isto significa no mundo real?
As entradas são, na verdade, indicadores de condições. Vou dar uma série de exemplo para ficar mais claro: se são 17h; se a caixa d’água está cheia; se a porta do carro está fechada; se a temperatura é maior que 30ºC; se um botão foi pressionado…
Ou seja, as entradas indicam o estado de alguma coisa do mundo real. No momento, você não precisa se preocupar em saber qual é o circuito que gera o sinal digital dizendo que “a caixa d’água está cheia” por exemplo.
Pois, para montar estes circuitos, é necessário utilizar a eletrônica analógica, sistemas embutidos ou até a própria eletrônica digital. E, não é objetivo deste curso falar sobre isso no momento. Portanto, trataremos estes circuitos como caixas pretas que informam o estado das coisas com sinais digitais (0 ou 1).
Entretanto, o site possui conteúdo a respeito destas outras áreas que podem te ajudar a entender como fazer estes circuitos.
Lógica da entrada: positiva e negativa
As entradas de um circuito podem ter dois tipos de comportamento: lógica positiva e lógica negativa. A entrada possui lógica positiva se ela for 1 quando a condição foi cumprida, e 0 senão. E, lógica negativa, quando for o contrário.
Exemplo: uma entrada que informa se a porta do carro está fechada. Se ela for lógica positiva, a entrada será 1 se a porta está fechada e 0 se ela está aberta. E o contrário para a lógica negativa: 0 se a porta está fechada e 1 se a porta está aberta.
A entrada poderia ser “porta do carro aberta”, aí a lógica seria o contrário da analisada acima. Tudo depende de como a entrada é definida.
Criando circuitos combinacionais
Tendo em vista o significado real das entradas, o circuito combinacional serve para informar se um conjunto de condições foi atingido para que seja possível tomar uma decisão. Um exemplo bem simples:
Se uma das portas do carro (considerando um carro de 2 portas) estiver aberta (nível lógico 1) e o motor do carro estiver ligado (nível lógico 1), o circuito deve gerar um sinal de nível alto. E vamos supor que este sinal seja utilizado para acionar um alarme.
Ou seja, é um circuito com três entradas (uma para cada porta e o motor) e uma saída. E o propósito do circuito é alertar ao motorista sobre a porta aberta quando o carro estiver ligado.
Agora vamos às etapas de como criar um circuito combinacional:
Tabela-verdade – Entradas
O primeiro passo para criar o seu circuito combinacional é criar a tabela-verdade do circuito contendo todas as entradas e todas as saídas. Assim como foi visto na aula 4, as entradas e as saídas ficam separadas por colunas e as saídas ficam na parte direita da tabela.
As linhas abaixo das entradas devem contem todas as combinações possíveis das entradas na forma binária. A ideia aqui é imaginar que as entradas juntas formam um único número binário. E a quantidade de combinações é dada por:
Sendo n o número de entradas.
Entretanto, existe uma forma fácil de se fazer isto. Considerando as entradas como um único número binário, basta escrever, em ordem crescente, do numero 0 até o número máximo que é possível escrever com n bits.
Veja o exemplo abaixo das entradas da tabela-verdade com 4 entradas:
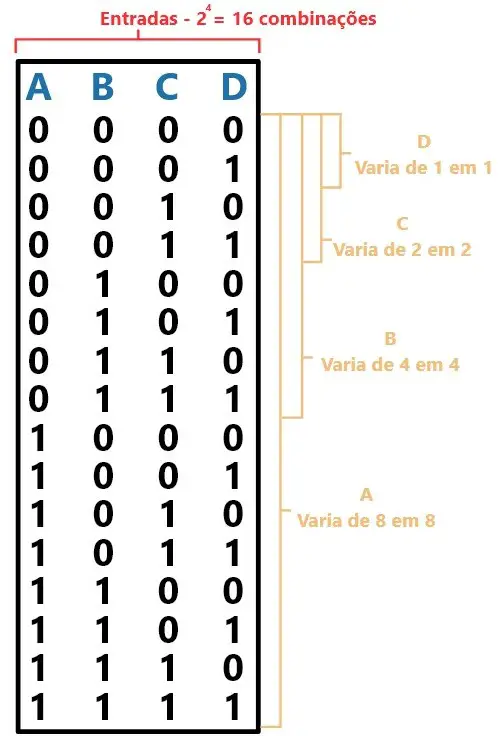
A tabela acima começou em 0 e terminou em 15 (1111) que é o número máximo que pode ser escrito com 4 bits. Enfim, pela própria imagem, dá para entender como fazer esta parte.
Tabela-verdade – Saídas
Depois de montar as entradas da tabela, basta escrever qual é o estado da(s) saída(s) para cada combinação da entrada. Veja o exemplo abaixo da tabela de um circuito com 2 entradas e 2 saídas:
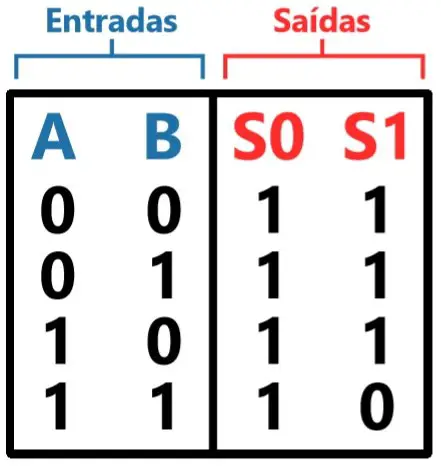
Vamos fazer algumas observações sobre a tabela acima:
A saída S0 é 1 para qualquer valor de A e B. Portanto, sua simplificação é simples: S0 = 1. E a saída S1 também é bem simples, pois ela apresenta o mesmo comportamento de uma porta NAND, logo: S1 = ¬(A.B).
Caso exista uma linha que é impossível de ocorrer, a saída para aquela linha deverá ser indicada por um X. Este X é chamado de don’t care e é um estado em que o valor da saída não importa (o nome já diz tudo), já que é impossível de ocorrer. Portanto, é um estado que pode ser tanto 0 quanto 1. Mais a frente veremos como lidar com ele.
A tabela-verdade do circuito acima é bem simples, mas como fazemos para obter a expressão final dos circuitos mais complexos? Adiante, veremos duas formas distintas de se obter as expressões finais dos circuitos digitais a partir da tabela-verdade.
Expressões da saída
As duas formas convenientes de apresentar as expressões booleanas da saída de um circuito são: a soma de produtos e o produto de somas. Elas também são chamadas de forma canônica.
A soma de produtos e o produto das somas são obtidos por meio da análise individual da expressão da saída em cada linha.
Soma de produtos (minitermos)
A soma de produtos nada mais é do que a saída expressa em uma soma de de vários termos. Termos estes que são as entradas multiplicadas entre si. Por exemplo (3 termos somados):
S = A.B + (¬A).B + (¬A).(¬B)
Cada termo somado é chamado de minitermo. O minitermo vem de uma linha da tabela-verdade em que a saída é igual a 1. Portanto, se a saída em uma tabela-verdade for igual à 1 em 7 linhas, haverão 7 minitermos.
O minitermo de uma linha é encontrado fazendo o produto entre o estado das entradas naquela linha ser igual à 1. Para exemplificar melhor, vamos pegar a tabela mostrada anteriormente:

O minitermo da primeira linha (m0) é o produto das entradas que faz gerar um nível lógico alto. Se A e B são 0, como o produto entre eles pode ser 1? Para isto, basta negar as duas entradas:
m0 = (¬A).(¬B)
No caso da segunda linha, A é 0 e B é 1. Para que o produto entre os dois seja 1, basta negar A:
m1 = (¬A).B
O mesmo raciocínio é feito para as demais linhas…
Desta forma, para obtermos a expressão booleana de uma saída, basta somar os minitermos da tabela-verdade das linhas em que a saída é igual a 1.
Por exemplo, a saída S1 da imagem anterior: ela é 1 nas linhas 0, 1 e 2. Portanto, a expressão de saída deverá ser a soma dos minitermos m0, m1 e m2:
S1 = (¬A).(¬B) + (¬A).B + A.(¬B)
Produto das somas (maxitermos)
O produto das somas é a saída expressa na forma de produto entre vários termos. Termos estes que são as entradas somadas entre si. Por exemplo (3 termos multiplicados):
S = (A + B) . (¬A + B) . (¬A + ¬B)
Cada termo multiplicado é chamado de maxitermo. O maxitermo vem de uma linha da tabela-verdade em que a saída é igual a 0. Portanto, se a saída em uma tabela-verdade for igual à 0 em 5 linhas, haverão 5 maxitermo.
O maxitermo de uma linha é encontrado fazendo a soma entre o estado das entradas naquela linha ser igual à 0. Pegando a tabela mostrada anteriormente novamente:

O maxitermo da primeira linha (M0) é a soma das entradas que faz gerar um nível lógico baixo. Se A e B são 0, fica muito fácil a soma entre eles ser 0, pois 0+0 = 0. Logo:
M0 = (A + B)
No caso da segunda linha, A é 0 e B é 1. Para que a soma entre os dois seja 0, basta negar B:
M1 = (A + ¬B)
O mesmo raciocínio é feito para as demais linhas…
Desta forma, para obtermos a expressão booleana de uma saída, basta multiplicar os maxitermos da tabela-verdade das linhas em que a saída é igual a 0.
Por exemplo, a saída S1 da imagem anterior: ela é 0 apenas na linha 3. Portanto, a expressão de saída deverá ser o próprio maxitermo m3 (não há produto, pois existe apenas um maxitermo):
S1 = (¬A + ¬B)
Don’t care
Como foi comentado anteriormente de maneira breve, o don’t care (X) é quando o estado da saída em uma linha não importa, pois aquela linha é impossível de ocorrer.
Neste contexto de minitermos e maxitermos, o don’t care pode ser tratado tanto como 0, quanto como 1. Portanto, adote ele como 0 ou 1 de acordo com o que irá simplificar ao máximo sua saída.
Simplificando a saída
Considerando que S1 possui a mesma saída que a porta NAND: É possível perceber que as expressões finais para os exemplos mostrados na soma de produto e no produtos das somas ainda estão estranhas.
No primeiro caso, a expressão final ainda está muito grande, pois não foi simplificada. E, no segundo caso, a expressão não se parece com uma porta NAND.
Se formos simplificar os minitermos do 1º exemplo, chegaríamos ao maxitermo do 2º exemplo. Entretanto, a expressão (¬A + ¬B) ainda não é igual a uma porta NAND. Acontece que ela é equivalente e funciona da mesma forma, de acordo com o teorema de De Morgan.
Para comprovar que as duas são equivalentes, você pode aplicar o teorema de De Morgan na expressão (negar ela duas vezes):
(¬A + ¬B) = ¬¬(¬A + ¬B) = ¬(¬¬A . ¬¬B) = ¬(A.B)
Sobre a utilização dos minitermos ou maxitermos, em muitos casos, é interessante optar por aquele que terá a menor quantidade de termos no fim das contas.
Nos exemplos anteriores, a saída S1 apresenta apenas 1 maxitermo e 3 minitermos, portanto, é preferível obter a expressão de saída em maxitermos. Tanto é que o caminho dos minitermos deu mais trabalho, pois foi necessário simplificar a expressão.
Para simplificar a expressão é necessário conhecer as simplificações da álgebra booleana, que foram mostrados na aula anterior. Entretanto, erros de simplificação podem levar à uma expressão mais extensa do que o necessário.
Para resolver parte deste problema, existe uma forma de simplificação interessante que veremos na próxima aula (Mapa de Karnaugh).
Exemplo de como projetar um circuito combinacional
Vamos utilizar o mesmo exemplo do carro citado anteriormente. Criar um circuito para ligar um alarme para avisar o motorista de um carro que uma das portas está aberta quando o motor do carro estiver ligado. O carro possui apenas 2 portas.
Entradas
Vou estipular as entradas de forma arbitrária com lógica positiva:
- P1 = porta 1 aberta. Se P1 = 1 a porta está aberta.
- P2 = porta 2 aberta. Se P2 = 1 a porta está aberta.
- M = motor ligado. Se M = 1 o motor está ligado.
Eu poderia ter utilizado as letras A, B e C como fiz ao longo do post, mas é interessante utilizar letras que remetem ao que elas estão representando. Isso facilitará o entendimento da tabela.
Saída
O circuito possuirá apenas 1 saída que será representada pela letra S mesmo. Para descobrir em quais linhas da tabela-verdade ela será 1, basta voltar às especificações do problema. É neste ponto que devemos tomar cuidado com a interpretação de texto.
A saída será 1 quando uma das portas estiver aberta (P1 = 1 OU P2 = 1) E quando o motor estiver ligado (M = 1). Portanto, basta achar em quais linhas da tabela estas condições são verdade.
Dependendo do circuito, só com a especificação acima, você já acha a expressão de saída (repare no OU e no E em negrito).
Criando tabela verdade
Relembrando, como são 3 entradas, haverão 2³ = 8 possibilidades. Irei colocar as entradas na tabela verdade em uma ordem qualquer de colunas. E, para cada linha, irei preencher a saída conforme descrito acima.

Expressão de saída
A tabela-verdade nos mostra que existem 3 minitermos e 5 maxitermos. Portanto, é mais razoável achar a expressão de saída em termos de soma de produtos.
Sendo assim, a saída será a soma dos minitermos m3, m5 e m7:
S =
.P2.M + P1.
.M + P1.P2.M
Simplificando a expressão de saída
Agora, vamos simplificar a expressão de saída. Vou começar colocando P1.M em evidência:
S =
.P2.M + P1.M(
+ P2)
¬P2 + P2 = 1 pela propriedade de adição, logo:
S =
.P2.M + P1.M
Colocando M em evidência:
S = M(
.P2+ P1)
Lembrando que A + ¬AB = A +B, logo:
S = M(P1 + P2)
Portanto, chegamos a uma simplificação máxima da expressão de saída. É possível deixar a saída no formato acima, ou então multiplicar o M pela expressão dentro do parêntese e obter:
S = M.P1 + M.P2
As duas expressões são logicamente equivalentes. E, sempre que possível, dê uma conferida na sua expressão simplificada para ver se ela está coerente com a tabela. Para isso, insira os valores da tabela nela e veja se a saída é a esperada.
Montando o circuito combinacional
O último passo é montar o circuito de acordo com a expressão de saída. Para isso, utilizarei a expressão:
S = M(P1 + P2)
Será um OR entre P1 e P2 e uma AND entre este resultado e o M. Desta forma, o circuito da expressão acima está representado abaixo:
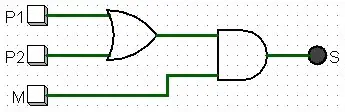
A partir da imagem acima, podemos perceber que o circuito final é bem pequeno, pois a simplificação reduziu bastante o número de portas lógicas necessárias.
Observações finais
Com os passos mostrados neste post, você já pode começar a projetar seus próprios circuitos digitais utilizando os Circuitos Integrados mostrados na aula 4.2.
Uma excelente dica que posso dar é o programa Logisim, que te permite construir e simular circuitos digitais. Inclusive, foi ele que utilizei para desenhar os circuitos que mostrei nesta aula e na passada.
Enfim, as simplificações podem ser um pouco trabalhosas e podem gerar erros no circuito final. Por conta disso, iremos aprender, na próxima aula, um método bem interessante de simplificação que facilita bastante o processo de achar a expressão de saída. O nome do método é mapa de Karnaugh.
E, após aprender sobre o mapa de Karnaugh, iremos montar um circuito combinacional na prática utilizando os CIs das portas lógicas.
Mapa de Karnaugh – Aula 6.1 – ED

Gostei da forma simples e transparente de explicar. Facilitou o entendimento.
Que ótimo, Paulo! Espero que goste dos demais assuntos do site.