O amplificador operacional permite a criação de circuitos bem úteis. Sendo assim, neste post, veremos alguns circuitos típicos que podem ser criados com ele.
Informações importantes
Se você deseja aprender o que é o amplificador operacional e como ele funciona, leia o post sobre.
Neste post, pretendo mostrar alguns circuitos “padrões” que utilizam os amplificadores operacionais. É claro que, existem muitas outras configurações além das que mostrarei, mas o estudo delas parte do mesmo princípio, conforme veremos adiante.
E é importante mencionar que os amplificadores serão considerados ideais e serão desenhados sem as entradas de alimentação. Isto, porque estarei considerando que ele está sendo alimentado por uma fonte simétrica (ex: +15V e -15V ou +12V e -12V).
Por fim, o objetivo de algumas análises será obter uma relação entre a tensão de saída (vO) e a tensão de entrada (vI), chamada de função de transferência.
Comparador
Esta é a configuração mais simples do amplificador operacional e é muito utilizada em circuitos digitais.
Circuito e função de transferência
O circuito do comparador consiste apenas do amplificador operacional na sua forma padrão. Veja o circuito abaixo:
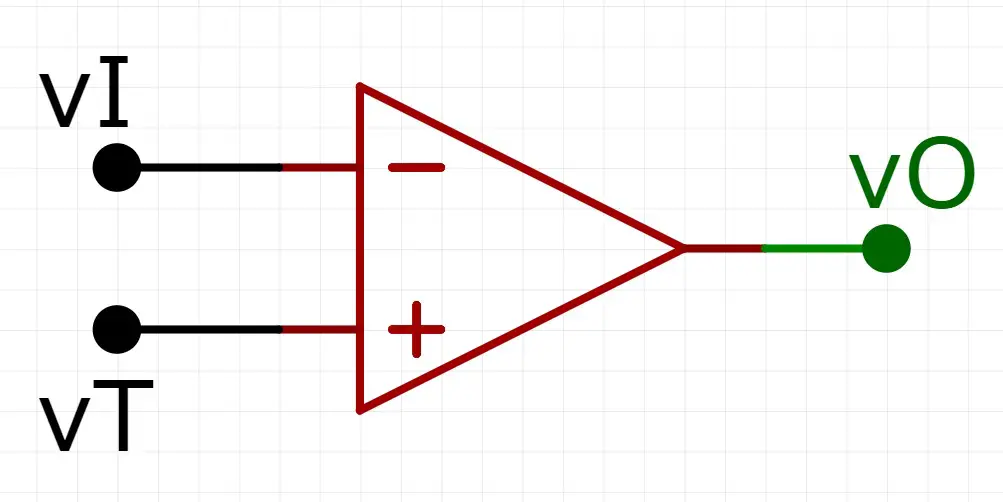
Como é sabido, para o amplificador ideal, temos:
1) Se vD = 0, então vO = 0
2) Se vD > 0, então vO = Vcc
3) Se vD < 0, então vO = Vee
E:
vD = vP – vN = vT – vI
Ou seja:
1) vO = Vcc se vI < vT
2) vO = Vee se vI > vT
Portanto, este circuito, como o nome diz, funciona como um comparador de tensões. Num caso prático, coloca-se uma tensão fixa em uma das entradas (vT por exemplo) e a outra é ligada no circuito que se deseja monitorar. A imagem abaixo ilustra a função de transferência do comparador (vI é a entrada):
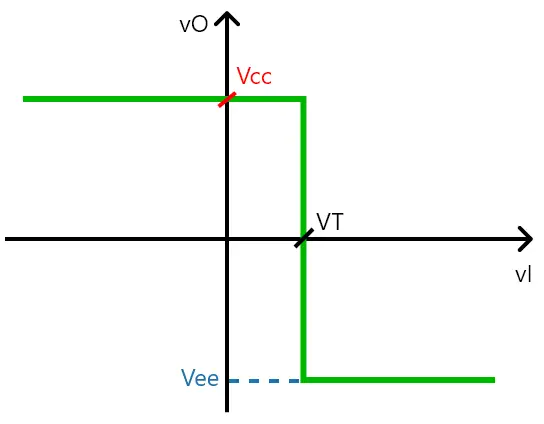
No caso dos circuitos digitais, faz sentido utilizar este circuito com Vcc = 5V e Vee = 0. Pois, dessa forma, a saída do comparador indicará seu estado em binário: 0 (0V) ou 1 (5V).
Aplicações e observações
O comparador é bem útil e pode ser encontrado no circuito do versátil CI 555. Além disto, eles podem ser utilizados também em conversores analógico-digital.
É possível encontrar os comparadores em muitos outros circuitos, mas ele pode aparecer em um formato diferente, que é o caso do comparador com histerese. Não pretendo explicá-lo em detalhes aqui, mas vale uma breve descrição:
O comparador com histerese possui uma realimentação positiva. O que acaba permitindo ao circuito trabalhar com dois valores de comparação diferentes. Um valor é usado para comparar a entrada quando a saída está saturada negativamente (Vee) e outro para quando a saída está saturada positivamente (Vcc).
Estes dois valores de comparação servem para manter a saída estável quando o sinal de entrada apresenta pequenas oscilações, que poderiam fazer a saída ficar oscilando se houvesse um único limiar de comparação.
Amplificador operacional inversor
Esta é uma configuração muito comum de ser encontrada nos circuitos com amplificador operacional.
Circuito e função de transferência
O circuito do inversor é composto por um amplificador com realimentação negativa realizada por um resistor. Veja adiante:
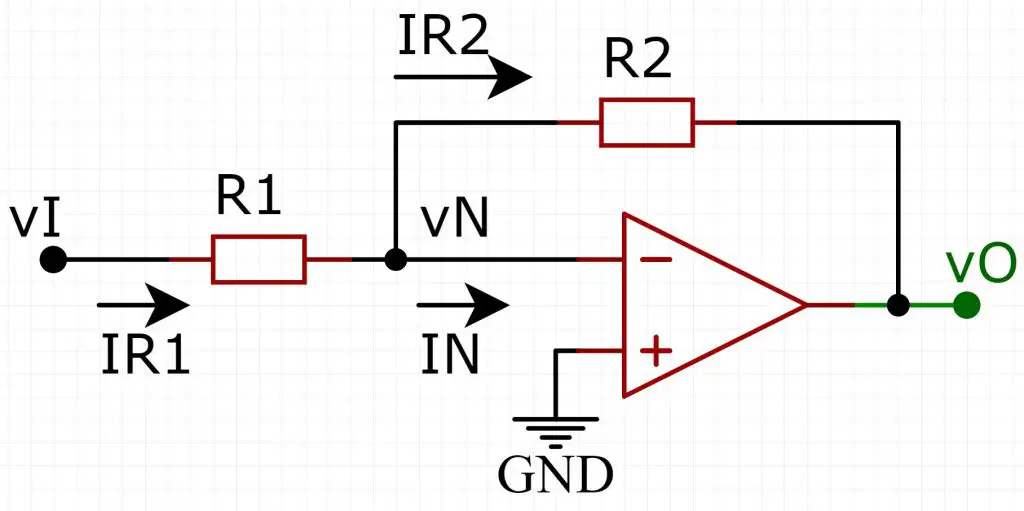
Pode parecer complexo a princípio, mas é um circuito bem simples até. Para começar a análise, primeiro, vamos aplicar a Lei de Kirchhoff das correntes no nó onde está a tensão vN (nó da entrada inversora):
IR1 = IR2 + IN
Como é sabido, para o amplificador ideal, a corrente nas entradas inversora ou não-inversora é 0. Então:
IR1 = IR2
Destrinchando a equação pela lei de Ohm, temos:
\frac{vI – vN}{R1} = \frac{vN – vO}{R2}
Para ir além deste ponto, é necessário lembrar de um conceito muito importante, que é o do curto-circuito virtual. E, para que ele seja válido, a realimentação tem que ser negativa e o amplificador não pode estar saturado. A realimentação é de fato negativa, e podemos admitir que ele não esta saturado e progredir com a análise para ver se o cálculo será consistente.
Sendo assim, para o curto-circuito virtual, vP = vN. E vP = 0, então vN = 0:
\frac{vI}{R1} = \frac{-vO}{R2}
Reescrevendo a equação para obter a função de transferência:
\frac{vO}{vI} = -\frac{R2}{R1}
Diante da equação acima, é perceptível que o sinal de saída é dado por uma relação entre as resistências R2 e R1 e ele tem polaridade oposta ao do sinal de entrada, por isso o nome amplificador inversor.
Por fim, o gráfico da função de transferência está ilustrado adiante:
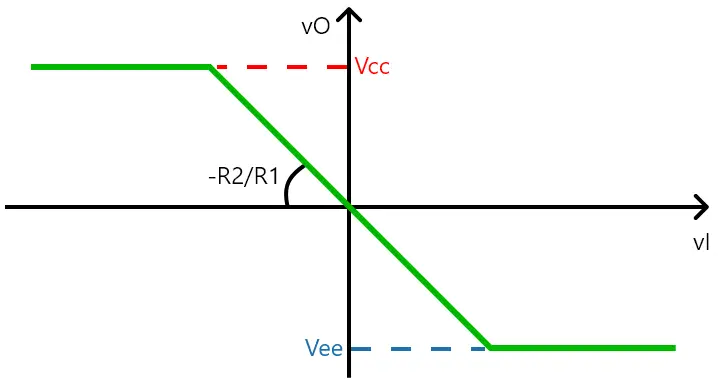
Aplicações e observações
Este tipo de circuito se aproveita da linearidade do amplificador operacional, pois é esta a zona de interesse do inversor. Neste sentido, o inversor pode ser utilizado para amplificar tensões e serve até como um multiplicador matemático.
A inversão de polaridade pode ser algo não desejado em algumas aplicações, mas, em outras, isto garante uma inversão de fase do sinal de entrada, o que pode ser útil.
Buffer ou amplificador seguidor de tensão
O Buffer é bem semelhante ao amplificador inversor, pois este é como se fosse o circuito do inversor com R1 e R2 iguais a 0.
Circuito e função de transferência
Diante do mencionado acima, o circuito do Buffer consistirá apenas do amplificador operacional com uma realimentação negativa direta e a entrada (vI) sendo ligada na entrada não-inversora do amp op. Veja abaixo:
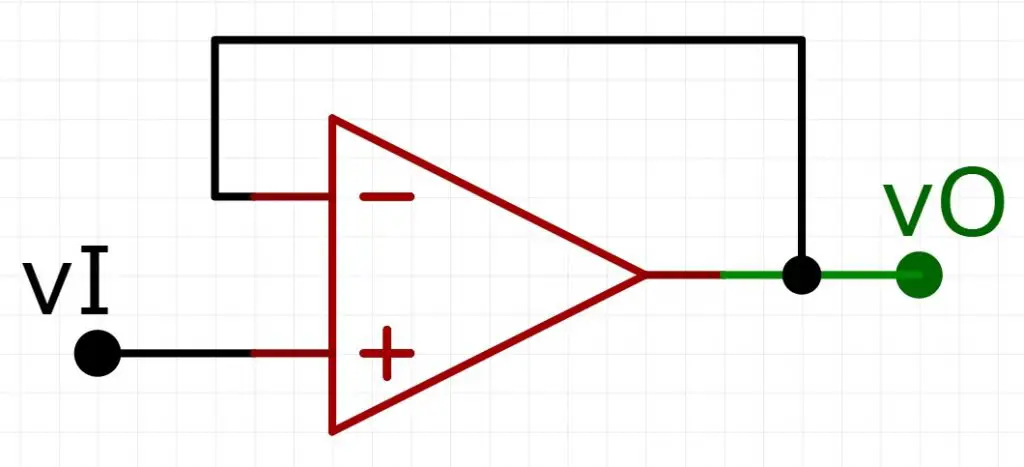
Para a análise do Buffer, podemos aplicar o mesmo princípio do curto-circuito virtual de antes (respeitando as condições). Sendo assim:
vP = vN = vI
Porém:
vN = vO
Então:
vI = vO
E a função de transferência é apenas (ganho unitário):
\frac{vO}{vI} = 1
Aplicações e observações
Pode parecer sem sentido este tipo de configuração, mas o Buffer pode ser útil para amplificar a corrente do sinal de entrada. Isso, porque o sinal de saída será igual ao de entrada em termos de tensão, mas a corrente fornecida dependerá da capacidade máxima do amplificador operacional usado.
No caso de um microcontrolador, por exemplo, sua saída digital pode ter um limite de 20mA, o que o impede de acionar diretamente algumas cargas. Mas, se o pino digital for ligado a um Buffer, o microcontrolador poderá comandar cargas de maiores correntes.
Além disto, o Buffer tem a propriedade de isolar o circuito de entrada da saída, podendo ser usado para proteção. E uma outra utilidade ainda é o casamento de impedâncias, pois a resistência de saída é idealmente nula, o que ajuda se o objetivo for ligar um circuito de alta impedância em um circuito de um fone de ouvido por exemplo (baixa impedância).
Amplificador operacional não-inversor
Como o nome indica, esta configuração é “contrária” a do amplificador inversor.
Circuito e função de transferência
O circuito não-inversor é semelhante ao do amplificador inversor com a diferença que o resistor R1 é ligado ao terra e a entrada (vI) é ligada na entrada não-inversora:
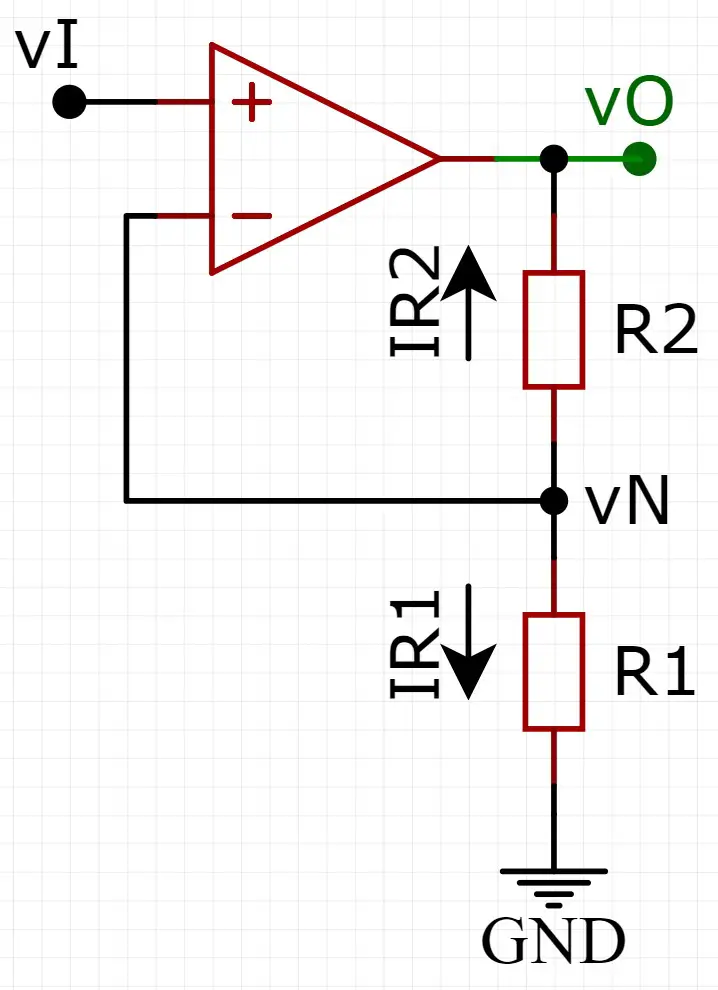
E a análise deste circuito também é bem semelhante. Vamos aplicar a Lei de Kirchhoff das correntes no nó onde está a tensão vN (nó da entrada inversora). Para isto, já vou considerar que não há corrente entrando no amplificador:
IR1 + IR2 = 0
Destrinchando a equação pela lei de Ohm, temos:
\frac{vN – 0}{R1} + \frac{vN – vO}{R2} = 0
Agora, basta aplicar o conceito do curto-circuito virtual respeitando as condições (considerando o amp op não saturado). Sendo assim vN = vP = vI e:
\frac{vI}{R1} + \frac{vI-vO}{R2} = 0
Manipulando a equação para obter a função de transferência:
\frac{vO}{vI} = 1 + \frac{R2}{R1}
Assim como no inversor, aqui o sinal de saída é igual ao sinal de entrada multiplicado por uma constante. Porém, neste caso, a constante é obrigatoriamente maior que 1 e a polaridade não é invertida (por isto o nome é não-inversor).
Por fim, o gráfico da função de transferência está ilustrado adiante (é um espelho do gráfico do inversor):
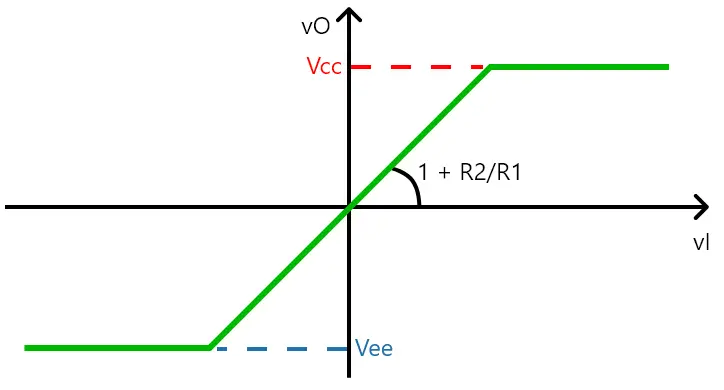
Observações
As mesmas observações do amplificador inversor são válidas aqui. A diferença é que este circuito não apresentará inversão de fase, o que pode ser útil em alguns casos.
Amplificador operacional somador inversor
A configuração do somador faz jus ao nome do amplificador operacional, pois serve para fazer uma operação de soma entre dois ou mais valores de tensão.
Assim como está indicado em seu nome, a tensão de saída terá polaridade invertida em relação a tensão de entrada. Para criar um somador não-inversor o princípio é parecido com o do amplificador não-inversor. E não pretendo mostrá-lo aqui.
Outra solução possível é adicionar um circuito inversor na saída do somador.
Circuito e expressão de saída
O circuito do somador é igual ao do amplificador inversor, porém com a adição de mais entradas (vI2, vI3…). Este circuito tem a capacidade de somar quantas entradas forem desejadas, então a quantidade pode variar de acordo com a necessidade. Vou mostrar um circuito com N entradas, sendo N um número inteiro maior que 1.
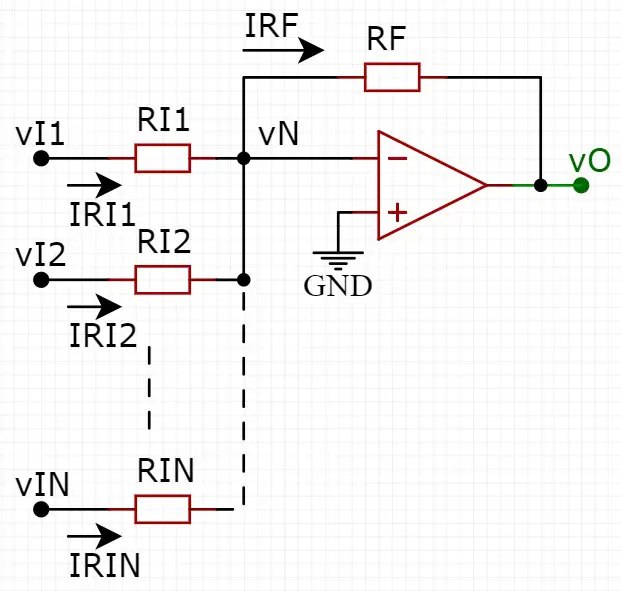
A avaliação deste circuito segue o mesmo princípio do amplificador inversor. Enfim, aplicando a Lei de Kirchhoff das correntes no nó onde está a tensão vN (nó da entrada inversora). Para isto, já vou considerar que não há corrente entrando no amplificador:
IRI1 + IRI2 + … + IRIN = IRF
Destrinchando a equação pela lei de Ohm, temos:
\frac{vI1 – vN}{RI1} + \frac{vI2 – vN}{RI2} + … + \frac{vIN – vN}{RIN} = \frac{vN – vO}{RF}
Assim como foi discutido, pelo curto-circuito virtual, vN = vP = 0 (com as condições respeitadas). Então:
\frac{vI1}{RI1} + \frac{vI2}{RI2} + … + \frac{vIN}{RIN} = -\frac{vO}{RF}
Como existem várias entradas, não faz muito sentido achar uma função de transferência, faz mais sentido achar a expressão da tensão de saída. E isto pode ser feito isolando vO:
vO = -RF*[\frac{vI1}{RI1} + \frac{vI2}{RI2} + … + \frac{vIN}{RIN}]
Desta forma, é possível somar as entradas e atribuir um ganho diferente para cada uma. Mas, se você desejar criar um somador com ganho uniforme, é possível usar o mesmo valor (RI) de resistência para RI1, RI2 … e RIN:
vO = -\frac{RF}{RI}*(vI1 + vI2 + … + vIN)
Aplicações e observações
O amplificador somador permite a criação de mais um circuito que realiza operações matemáticas. Podendo ser utilizado para fazer contas.
Outra aplicação interessante do somador é um tipo de conversor digital-analógico. Pois, cada entrada pode possuir um ganho diferente e ser representada por um número binário. E, de acordo com o acionamento destes números binários, a tensão de saída varia, convertendo valores digitais em um analógico.
Amplificador operacional subtrator ou diferencial
Assim como o nome propõe, o subtrator é um circuito que serve para subtrair dois valores de tensão.
Circuito e expressão de saída
O circuito do subtrator parece com o do amplificador inversor com a adição de um divisor de tensão na entrada não-inversora. Veja abaixo:
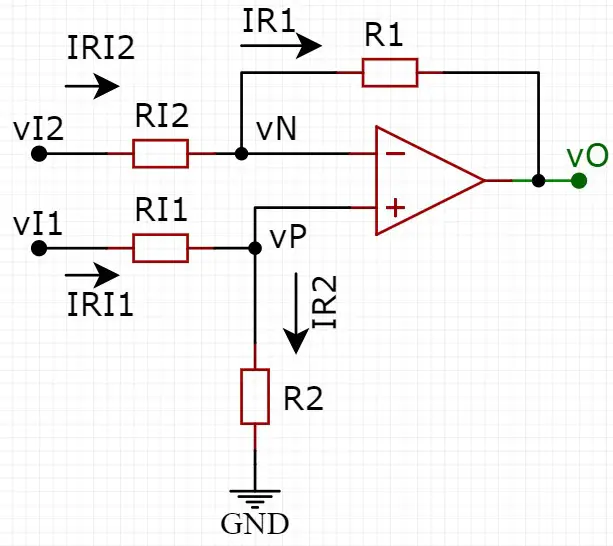
O desenvolvimento dos cálculos deste circuito é um pouco mais trabalhoso, pois existem dois nós que precisam ser considerados. Mas, ainda assim, é bem tranquilo. Primeiro, aplicando a Lei de Kirchhoff das correntes no nó onde está a tensão vN (nó da entrada inversora). Para este caso e os demais, já vou considerar que não há corrente entrando no amplificador:
IRI2 = IR1
Em seguida, destrinchando as duas expressões pela lei de Ohm:
\frac{vI2-vN}{RI2} = \frac{vN-vO}{R1}
Agora, para o nó da tensão vP, fica mais fácil resolver as contas se aplicarmos a fórmula de um divisor de tensão:
vP = \frac{vI1 * R2}{RI1 + R2}
E utilizando a simplificação do curto-circuito virtual, temos que vP = vN. Portanto, podemos aplicar a expressão acima na equação do nó de vN:
\frac{vI2-\frac{vI1 * R2}{RI1 + R2}}{RI2} = \frac{\frac{vI1 * R2}{RI1 + R2}-vO}{R1}
Depois de um algebrismo maluco, é possível chegar à seguinte expressão:
vO = vI1 * [\frac{R2}{RI1 + R2} * (1+\frac{R1}{RI2})] – vI2*[\frac{R1}{RI2}]
Diante da equação acima, é perceptível que a saída é resultado de uma subtração das entradas. Mas as entradas estão sendo multiplicadas por valores distintos o que pode não ser nada desejado. Sendo assim, é interessante igualar as constantes as quais elas estão sendo multiplicadas:
\frac{R2}{RI1 + R2} * (1+\frac{R1}{RI2}) = \frac{R1}{RI2}
Fazendo novamente um algebrismo com a equação acima, chega-se na seguinte condição:
\frac{RI2}{R1} = \frac{RI1}{R2}
Se esta condição for respeitada, a expressão da saída fica a seguinte:
vO = \frac{R1}{RI2} * (vI1 – vI2)
Ou seja, agora, a saída é de fato definida por uma subtração entre as tensões de entrada, cujo ganho pode ser definido pela relação dos resistores.
Aplicações
Além da aplicação como operador matemático, o subtrator pode ser muito útil na criação de sistemas analógicos de controle com feedback negativo.
Amplificador integrador
O amplificador integrador é um circuito poderoso, pois é capaz de realizar uma operação matemática relativamente complexa, que é a integração.
E vale destacar que a saída deste tipo de circuito varia com o tempo, mesmo que a entrada seja mantida constante. Isto é, este é um circuito dependendo do tempo.
Circuito e expressão de saída
Ao contrário do que foi visto até então, o circuito do integrador passa a utilizar um componente além do resistor, que, no caso, é o capacitor.
E este circuito é bem parecido com o do amplificador inversor, a diferença é que o resistor de realimentação é substituído por um capacitor.
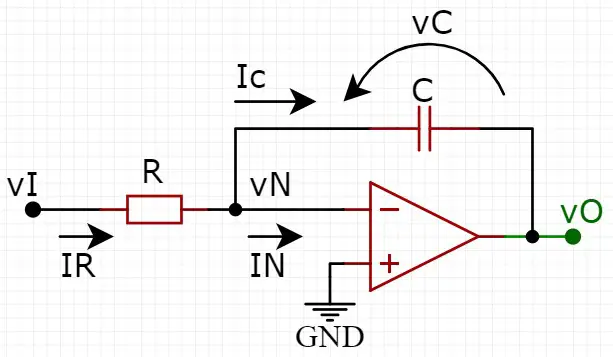
Devido a presença do capacitor, a expressão obtida no circuito deixa de ser algo linear e toma a forma de integrador. Primeiramente, vamos aplicar a Lei de Kirchhoff das correntes no nó da tensão vN (já considerando IN = 0 e vN = vP = 0):
IR = IC
Destrinchando a expressão de IR pela lei de Ohm, temos:
IC = \frac{vI-vN}{R} = \frac{vI}{R}
Em seguida, podemos contar com outra expressão importante (considerando vN o lado do terminal “positivo do capacitor”):
vC = vN – vO = -vO
E a tensão em cima do capacitor é dada por:
vC(t) = \frac{1}{C} * \int_{ti}^{t} IC(t) dt + vC(ti)
O valor de IC da expressão de IR pode ser substituído acima:
vC(t) = \frac{1}{C} * \int_{ti}^{t} \frac{vI(t)}{R} dt + vC(ti)
Como R é constante, então pode ser tirado para fora da integral:
vC(t) = \frac{1}{RC} * \int_{ti}^{t} vI(t) dt + vC(ti)
Por fim, resta substituir vC(t) na expressão de vO:
-vO = \frac{1}{RC} * \int_{ti}^{t} vI(t) dt + vC(ti)
Ou:
vO = -\frac{1}{RC} * \int_{ti}^{t} vI(t) dt + vC(ti)
Portanto, a tensão de saída é resultado da integral da tensão de entrada, mais a tensão inicial no capacitor (vC(ti)) multiplicados por uma constante (-1/RC). Lembrando que, na análise, considerei o lado esquerdo do capacitor como a referência positiva.
Aplicações e observações
Obviamente, uma aplicação é a poderosa operação matemática de integração. E esta ferramenta é bastante útil em circuitos de controle.
Além do controle, os integradores são úteis nas aplicações que envolvem a geração de ondas (onda triangular, rampa etc).
Na hora de se utilizar um integrador na prática é recomendável colocar um resistor em paralelo com o capacitor para evitar a saturação da saída e possibilitar um controle de ganho ao circuito.
Amplificador derivador ou diferenciador
Bem como o integrador, o derivador é uma ótima ferramenta que realiza a derivada do sinal de entrada. E sua saída também é dependente do tempo.
Circuito e expressão de saída
O circuito do derivador é próximo ao do integrador, porém com o capacitor trocado de lugar com o resistor. Veja adiante:
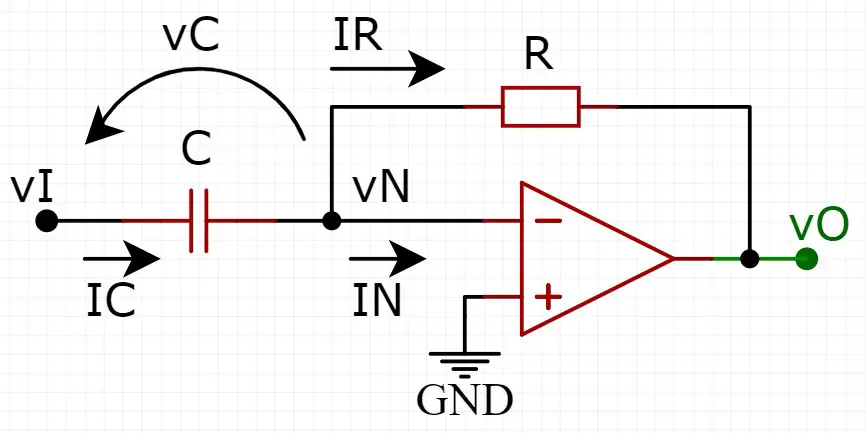
Conforme foi visto no tópico anterior, a adição do capacitor tira a linearidade do circuito e o mesmo é aplicável aqui, até mesmo para os cálculos. Para obter a expressão de saída vamos começar aplicando a Lei de Kirchhoff das correntes no nó da tensão vN (já considerando IN = 0 e vN = vP = 0):
IC = IR
Destrinchando a expressão de IR pela lei de Ohm, temos:
IC = \frac{vN-vO}{R} = -\frac{vO}{R}
Após isso, podemos substituir IC pela equação da corrente em um capacitor:
C \frac{dvC}{dt} = -\frac{vO}{R}
E a tensão vC também pode ser escrita como:
vC = vI – vN = vI
Portanto, fazendo a devida substituição, teremos a seguinte expressão de saída:
C \frac{dvI}{dt} = -\frac{vO}{R}
Ou:
vO = – RC \frac{dvI}{dt}
Portanto, a tensão de saída é resultado da derivada da tensão de entrada multiplicada por uma constante (-RC). É importante citar que, na análise, considerei o lado esquerdo do capacitor como a referência positiva.
Aplicações
As aplicações são bem próximas ao do amplificador integrador, pois o derivador pode ser utilizado como: um operador matemático; um circuito de controle; e como uma peça fundamental na geração de sinais (onda quadrada, impulso etc).
Outras configurações interessantes
Além do que foi mencionado, o amplificador operacional pode ser utilizador para:
- Gerar vários tipos de sinais.
- Como: onda quadrada, senoide, onda triangular…
- Converter tensão em corrente ou vice-versa.
- Criar filtros poderosos.
- Criar um multiplicador de tensões analógico.
- Por meio de um arranjo de um circuito exponencial e logarítmico.
E, ao longo do post, deve ter dado para perceber que as análises dos circuitos com amp op seguem o mesmo princípio (Lei de Kirchhoff).
Amplificador Operacional – O que é e como funciona

esse post foi muito intrigante, interessante e no final satisfatório, pois aprendi muito com esse post, que é muito interessante e cheio de aprendizado.
Show de bola! Muito obrigado pelo comentário poético hehe.
Muito obrigado pelo post.
Estava precisando aplicar um Amp-Op integrador em função do tempo. só preciso remodelar os arranjos matematicos para me entregar alguns valores conforme vou modificando o circuito.
Olá, Hudson. Por nada!
Te desejo sorte, pois a teoria dessa parte de circuitos de amp op parece ser bem simples, mas na prática surgem alguns efeitos indesejados que dificultam demais o projeto. Principalmente no circuito do integrador que a saída tende a aumentar indefinidamente.