A álgebra booleana é extremamente útil no desenvolvimento de sistemas digitais, principalmente para a simplificação de expressões. Com isto em vista, nesta aula iremos ver o que ela é e como utilizá-la.
Na aula anterior, aprendemos sobre os Circuitos Integrados das portas lógicas.
Informações básicas
Expressões booleanas
Quando estamos desenvolvendo um sistema digital, nos deparamos com expressões que regem o estado da saída do circuito em função do estado da(s) entrada(s). E essas expressões são chamadas de expressões booleanas.
Elas são baseadas nas operações das portas lógicas, conforme foi abordado na aula 4. Então, imagine que a saída (S) de um determinado circuito digital de duas entradas (A e B) é dada pela expressão:
S = A + B + AB + A
O + da expressão acima representa uma porta OR e as entradas juntas (AB) representam a porta AND. Portanto, o circuito acima, poderia ser representado da seguinte forma:
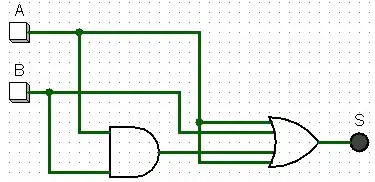
Utilidade da simplificação
O exemplo anterior é bem simples, pois foi necessário utilizar apenas duas portas lógicas para criá-lo. Porém, ele pode ser simplificado e, portanto, precisar de menos portas lógicas.
Se você analisar um pouco a expressão irá reparar que certos elementos são redundantes. Sendo mais específico, é o caso da entrada A sendo ligada duas vezes na porta OR (A+A). Se A = 0 -> A+A = 0; e se A = 1 -> A + A = 1.
Não é difícil de concluir que este processo é redundante e que o resultado final é o mesmo se a entrada for ligada uma vez ou infinitas vezes (A + A + A + … = A). Desta forma, poderíamos simplificar a expressão anterior para o seguinte formato:
S = A + B + AB
Entretanto, ela ainda possui redundâncias. E é sempre interessante simplificar as expressões para reduzir o circuito, facilitando assim, a montagem e também diminuindo o custo do projeto.
Esta outra redundância pode não ser nada intuitiva a princípio. Para esta finalidade, existe a álgebra booleana, que contém um conjunto de “regras” (axiomas) que podem ser aplicadas às expressões de maneira fácil para simplificá-las.
E este conjunto de “regras” pode ser desmembrado entre os teoremas de Boole e os teoremas de De Morgan. Adiante veremos o que dizem ambos.
Teoremas de Boole
Lembrando que o nível lógico baixo será tratado como 0 e o nível lógico alto será tratado como 1. E a negação será representada pelo símbolo ¬ para facilitar a escrita.
Para entender 100% dos axiomas que serão apresentados, faça tabelas-verdade para comprovar seu funcionamento.
Uma variável
Complemento
A negação dupla de uma variável é ela mesma:
- ¬(¬A) = A
Adição (OR)
- A + 0 = A
- A + 1 = 1
- A + A = A
- A + (¬A) = 1
Multiplicação lógica (AND)
- A.0 = 0
- A.1 = A
- A.A = A
- A.(¬A) = 0
Duas variáveis ou mais
Comutatividade
- A + B = B + A
- A.B = B.A
Associatividade
- A + (B + C) = (A + B) + C = A + B + C
- A . (B . C) = (A . B) . C = A . B . C
Distributividade
- A + (B.C) = (A + B).(A + C)
- A.(B + C) = AB + AC
- (A + B).(C + D) = AC + AD + BC + BD
A expressão 1 acima pode ser facilmente entendida se for feita de trás para frente:
(A + B).(A + C) = A.A + A.C + BA + BC
Colocando A em evidência:
A(1 + C + B) + BC
A expressão multiplicada por A dá 1, devido à propriedade de adição mostrada anteriormente (A + 1 = 1). Portanto:
A(1 + C + B) + BC = A.1 + BC = A + BC
Propriedades específicas
- A + AB = A
- A + (¬A.B) = A + B
Para validar a expressão 1 acima, basta colocar A em evidência:
A(1 + B)
Como 1 + B = 1:
A(1) = A
Já a expressão 2, advém da propriedade de distributividade:
A + (¬A.B) = (A + ¬A).(A + B) = 1.(A+B) = A + B
Observação
Podem existir outras expressões, mas serão apenas consequência das regras apresentadas neste tópico. Desta forma, com as regras apresentadas até então, você já é capaz de simplificar praticamente qualquer expressão.
Teoremas de De Morgan
Os teoremas de De Morgan não são intuitivos, pois apresentam uma equivalência entre dois tipos de expressões.
=
.
=
+
Forma de aplicar
Para facilitar a visualização dos axiomas acima, basta pensar que a barra está sendo distribuída entre cada elemento da expressão. Por exemplo, na primeira expressão:
A barra é distribuída em A, B e sobre o +. Portanto, A e B ficam barrados, mas o elemento + troca para multiplicação. É como se o contrário da soma (OR) fosse a multiplicação (AND) e vice-versa. O mesmo se aplica à segunda expressão.
Veja o que foi falado acima na imagem abaixo:
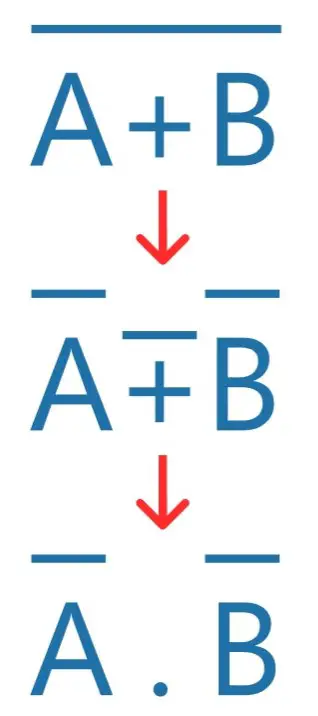
A barra de negação não pode ser aplicada diretamente em um operador como foi feito na imagem acima, mas o objetivo da imagem é ilustrativo.
Aplicação do teorema de De Morgan
Além da simplificação de expressões booleanas, o teorema de De Morgan tem outra aplicação muito importante: converter as portas lógicas do circuito.
Sendo mais claro: vamos pensar em uma determinada situação em que precisamos criar um circuito digital, mas só temos portas lógicas NAND à disposição. É bastante improvável que a sua simplificação resulte em expressões que envolvam apenas portas NAND.
Portanto, o ideal seria converter o seu circuito em expressões que façam uso apenas da porta NAND. E é neste ponto que os teoremas de De Morgan são úteis. Pois, bastaria negar duas vezes a expressão que não está de acordo e distribuir as barras até chegar a uma expressão razoável.
Como A = ¬(¬A), não tem problema barrar duas vezes uma expressão, pois ela continua logicamente equivalente. Este processo é feito apenas para fazer a conversão.
Veja o exemplo abaixo de como converter a porta OR em uma porta NAND com entradas barradas:
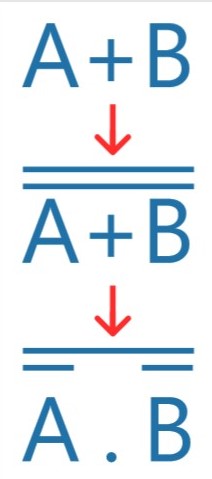
A expressão resultante é uma porta NAND, com as duas entradas barradas. E é seguindo esta lógica que podemos criar um circuito utilizando apenas portas NAND (ou NOR). Mais à frente, veremos como fazer isto de maneira apropriada.
Exemplo de aplicação da álgebra booleana
Considere a seguinte expressão da saída S de um determinado circuito:
S = AB
+ A
Colocando o A(¬C) em evidência:
S = A
(B +
)
A expressão B + (¬B) resulta em 1 de acordo com a propriedade de adição. Logo:
S = A.
.1
S = A
A partir da simplificação acima, conseguimos reduzir consideravelmente o circuito ao ponto de necessitar de apenas 2 portas lógicas. Sendo que, antes, iríamos precisar de 6. Veja o circuito resultante abaixo:
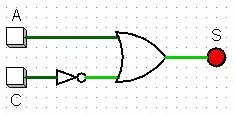
Considerações finais
A partir da álgebra booleana, já é possível ter uma noção de como começar a criar seus próprios circuitos digitais. Para se familiarizar com os axiomas, é importante fazer diversos exercícios de simplificação, como o do tópico anterior.
De toda forma, na aula seguinte, iremos finalmente aprender sobre a lógica combinacional, que é a lógica dos sistemas digitais que consideram os estados atuais das entradas para produzir uma saída. E, iremos resgatar muitas propriedades da álgebra booleana aqui mostrados.
Referência: Álgebra de Boole e Simplificação de Circuitos Lógicos
Circuito combinacional – Aula 6 – ED
