As portas lógicas são o fundamento da eletrônica digital, pois são elas que permitem a criação da lógica digital. Portanto, nesta aula, vamos aprender o que elas são e veremos sobre as portas lógicas elementares e as compostas.
Na aula anterior, aprendemos sobre os sistemas de numeração binário, octal e hexadecimal.
Definição
As portas lógicas são circuitos criados para manipular um bit ou um conjunto de bits em sua entrada de forma a fornecer um sinal (também binário) na saída de acordo com o estado dos bits da entrada.
Isto é, de acordo com o estado dos bits que estão na entrada, a saída da porta lógica pode ficar em nível baixo ou nível alto. Portanto, as portas lógicas, como o próprio nome sugere, permitem criar uma lógica digital a partir dos bits de entrada.
Apesar de ser possível imaginar inúmeras portas lógicas diferentes que manipulam bits de entrada para produzir uma saída específica, existem 3 portas lógicas elementares que, quando combinadas, são responsáveis por criar praticamente qualquer lógica digital. E elas são:
- Porta NOT
- Porta OR
- Porta AND
A definição será melhor entendida no tópico onde falaremos sobre as portas lógicas acima.
Tabela verdade
Um conceito muito importante e necessário é o de tabela verdade. Simplificadamente, tabela verdade é uma tabela que mostra o sinal de saída de um circuito lógico a partir dos sinais de entrada.
Seguindo a explicação de porta lógica, a tabela verdade de uma porta lógica mostra qual será a saída de acordo com o estado dos bits de entrada. Veja o exemplo de uma tabela abaixo.
| Bit de entrada 1 | Bit de entrada 2 | Bit de saída |
| 0 | 0 | 1 |
A tabela acima diz que, se os dois bits de entrada forem 0, a saída será 1. Uma tabela verdade completa deve mostrar todas as combinações possíveis dos bits de entrada e a saída para cada uma delas. No exemplo acima (2 bits de entrada), existem 4 combinações possíveis.
E é comum representar os bits de entrada com letras maiúsculas começando da letra A, sendo o bit A o mais significativo da entrada (se a entrada representar um único número binário). E é comum representar a saída com a letra S ou X.
E um circuito lógico pode ter mais de uma saída. Mas, como estamos falando de porta lógica, representei a tabela com apenas uma saída.
Portas lógicas elementares
Conforme dito, existem 3 portas lógicas elementares, que são:
Porta NOT
A porta NOT possui uma única entrada (1 bit) e ela é responsável por gerar um nível lógico na saída oposto ao nível lógico da entrada. Sendo assim, a tabela verdade desta porta lógica é:
| A (entrada) | S (saída) |
| 0 | 1 |
| 1 | 0 |
Esta operação feita pela porta NOT é chamada de negação/inversão (como o próprio nome sugere). E, para representar a negação, usa-se uma barra acima do bit que está sendo “invertido”. Com isto, outro termo muito utilizado para descrever a operação NOT é dizer que o bit foi “barrado”.
A imagem abaixo mostra o símbolo típico da porta NOT (triângulo com uma circunferência na ponta).
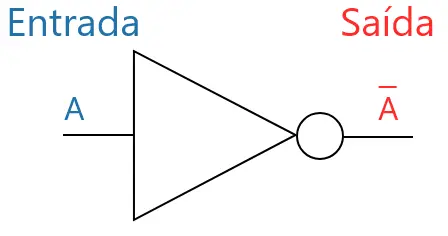
De acordo com a imagem acima, o bit de entrada A foi barrado pela porta NOT.
Porta OR
A porta OR possui no mínimo duas entrada (2 bits) e ela gera um nível lógico alto se pelo menos uma das entradas for 1. Sendo assim, a tabela verdade desta porta lógica é (para duas entradas):
| A | B | S |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Como o próprio nome sugere, a porta OR faz uma operação chamada “ou”. Isto é, a saída é 1 se a entrada A OU a entrada B for 1. E, para representar a operação “ou”, usa-se o símbolo de + entre os bits de entrada. Logo, a operação A “ou” B pode ser representada como A+B.
A imagem abaixo mostra o símbolo típico da porta OR (espécie de seta).
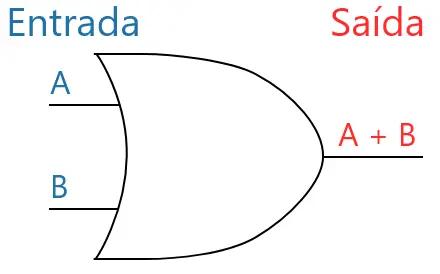
Um exemplo útil da porta OR é quando temos dois botões e desejamos que qualquer um dos dois acione um LED (ou alguma carga). Então, a porta OR acenderá o LED se o botão 1 OU o botão 2 for pressionado. Obviamente, se os dois forem pressionados, o LED será aceso da mesmo forma.
Por fim, podem ser encontradas portas OR com diversas entradas, mas a forma elementar dela é apenas com duas entradas.
Porta AND
A porta AND também possui no mínimo duas entrada (2 bits) e ela gera um nível lógico alto se todas as entradas forem 1. Sendo assim, a tabela verdade desta porta lógica é (para duas entradas):
| A | B | S |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Como o próprio nome sugere, a porta AND faz uma operação chamada “e”. Isto é, a saída é 1 se a entrada A E a entrada B for 1. E, para representar a operação “e”, usa-se o símbolo de vezes (ponto) entre os bits de entrada, ou então, eles são escritos juntos (sem espaçamento). Logo, a operação A “e” B pode ser representada como A.B ou AB.
A imagem abaixo mostra o símbolo típico da porta AND.
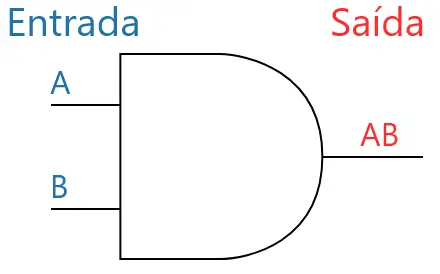
Um exemplo útil da porta AND é quando temos dois botões e desejamos que um LED (ou alguma carga) seja acionado APENAS se os dois botões forem pressionados juntos.
Por fim, podem ser encontradas portas AND com diversas entradas, mas a forma elementar dela é apenas com duas entradas.
Portas lógicas compostas
Como foi mencionado anteriormente, com apenas as 3 portas do tópico acima, é possível criar praticamente qualquer lógica digital. Entretanto, existem outras 4 portas muito úteis, que são formadas pela combinação das portas elementares.
São elas:
Porta NOR
A porta NOR é a combinação da porta OR com a porta NOT. Sendo assim, ela terá o mesmo funcionamento da porta OR, porém com a lógica da saída invertida: ela gera um nível lógico BAIXO se pelo menos uma das entradas for 1. A tabela verdade desta porta lógica é (para duas entradas):
| A | B | S |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Para representar a operação NOR, basta usar a mesma representação da porta OR, adicionando uma barra acima dos elementos da operação.
A imagem abaixo mostra o símbolo típico da porta NOR (porta OR com uma circunferência na ponta).
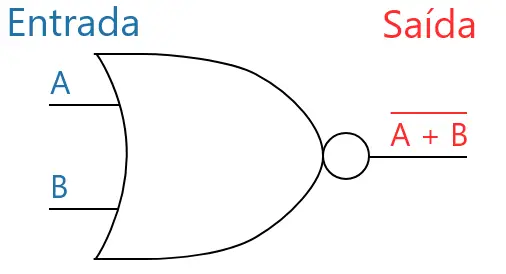
Porta NAND
Seguindo a mesma lógica da porta anterior, a porta NAND é a combinação da porta AND com a porta NOT. Logo, ela terá o mesmo funcionamento da porta AND, porém, com a lógica da saída invertida: ela gera um nível lógico BAIXO se todas as entradas forem 1. A tabela verdade desta porta lógica é (para duas entradas):
| A | B | S |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Para representar a operação NAND, basta usar a mesma representação da porta AND, adicionando uma barra acima dos elementos da operação.
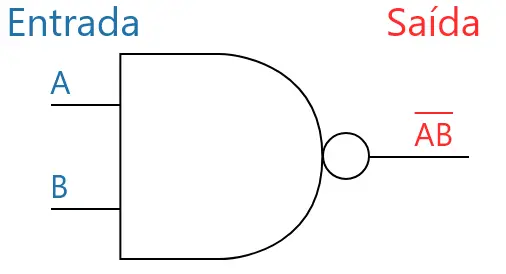
A imagem abaixo mostra o símbolo típico da porta NAND (porta AND com uma circunferência na ponta).
Porta XOR
Está porta lógica é chamada de XOR, ou então “OU exclusivo”. Ela gera um sinal de nível alto se os bits de entrada forem diferentes entre si.
A XOR é um pouco complexa, pois é formada por três operações lógicas, sendo duas ANDs e uma OR. A expressão que rege esta porta lógica está mostrada abaixo:
.B + A.
O circuito da expressão acima está mostrado na imagem abaixo:
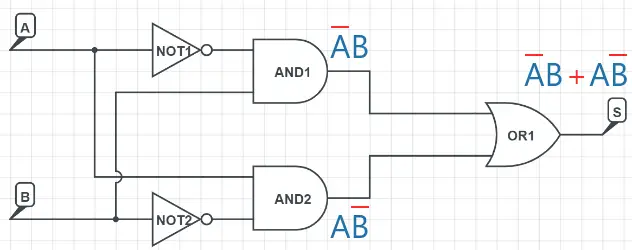
Caso surja alguma dúvida a respeito do circuito, reveja o funcionamento das portas lógicas elementares para relembrar também as representações das operações.
E a tabela verdade desta porta lógica é:
| A | B | S |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Para representar a operação XOR, é utilizado o símbolo da imagem abaixo (círculo ao redor do símbolo de soma):

Por fim, o símbolo típico da porta XOR está mostrado a seguir:
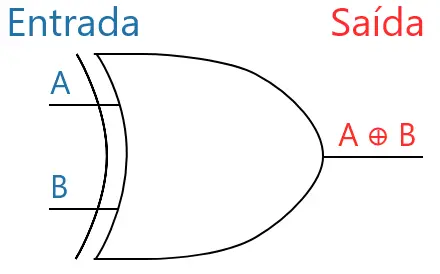
A princípio, esta porta parece ser sem proposito, mas ela será necessária de vez em quando em circuitos combinacionais (veremos futuramente). E a operação XOR é muito útil na operação bit a bit em programação (principalmente programação de microcontroladores).
Porta XNOR
Por fim, temos a porta XNOR, que é a combinação da porta XOR com a porta NOT. Desta forma, ela tem o mesmo funcionamento da porta XOR, porém com a lógica da saída invertida: ela gera um nível lógico BAIXO se os bits de entrada forem diferentes entre si. A tabela verdade desta porta lógica é:
| A | B | S |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Portanto, toda vez que os bits forem igual a 1, a saída é 1. Para representar a operação XNOR, é utilizado o símbolo da imagem abaixo (círculo ao redor de um ponto):

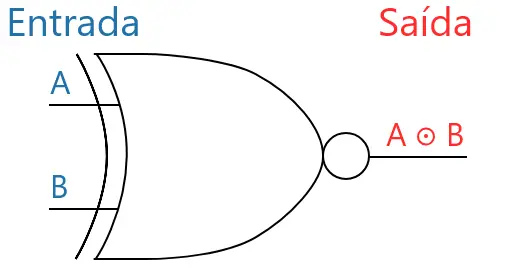
A imagem abaixo mostra o símbolo típico da porta XNOR (porta XOR com uma circunferência na ponta).
Considerações finais
É de extrema importância saber o funcionamento de cada porta lógica que foi mostrada no post. Pois, quando formos ver como criar um circuito combinacional (circuito digital simples), utilizaremos praticamente todas as portas citadas.
A próxima aula será um conteúdo complementar ao assunto, pois veremos o circuito por trás das portas lógicas. Não será um assunto obrigatório para o entendimento do conteúdo da eletrônica digital como um todo, mas é importante conhecê-lo.
Como as portas lógicas são feitas – Aula 4.1 – ED

muito bom as explicações
Muito obrigado!
Gostei muito, estava estudando essa materia, ai achei esse site para mais consultas, muito bom.
Que bom que gostou, Christian. Obrigado pelo comentário!